Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the Nagel point of a triangle
ResourceFunction["NagelPoint"][{p1,p2,p3}] returns the Nagel point of the triangle defined by vertices p1,p2 and p3. |
Find the Nagel point of three triangle vertices:
| In[1]:= |
| Out[1]= |
| In[2]:= | ![Graphics[{
{Orange, Opacity[0.2], Triangle[tri]},
TriangleConstruct[tri, {"Excircle", tri[[#]]}] & /@ {1, 2, 3},
HalfLine[{tri[[#]], na[[1]]}] & /@ {1, 2, 3},
{Thin, InfiniteLine[{#1, #2}]} & @@@ NestList[RotateLeft, tri, 2],
{
PointSize[
Scaled[0.08]],
Hue[0.58, 1, 1], na,
Text[
Style["Na", White, FontSize -> Scaled[0.04]],
Part[na, 1]]},
}, PlotRange -> {{-2.5, 7}, {-3, 6.5}}] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/46f/46f3a138-9a91-466a-874c-86b043303094/269833755b051dc9.png) |
| Out[2]= | 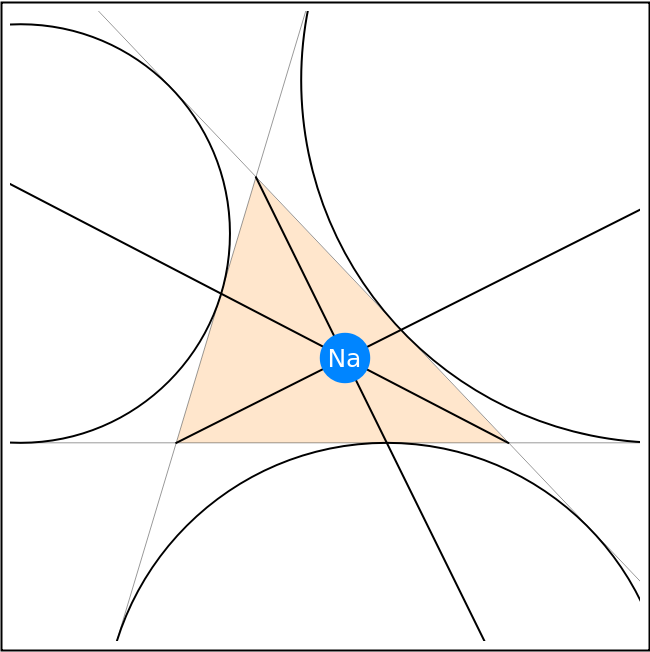 |
Compute the Nagel point of a 3D triangle:
| In[3]:= | ![tri = Triangle[{{0, 0, 0}, {1, 0, 0}, {0, 1, 1}}];
pt = Simplify[ResourceFunction["NagelPoint"][tri]]](https://www.wolframcloud.com/obj/resourcesystem/images/46f/46f3a138-9a91-466a-874c-86b043303094/1d532cfb01320cfb.png) |
| Out[3]= |
Show the Nagel point and the triangle together:
| In[4]:= |
| Out[4]= | 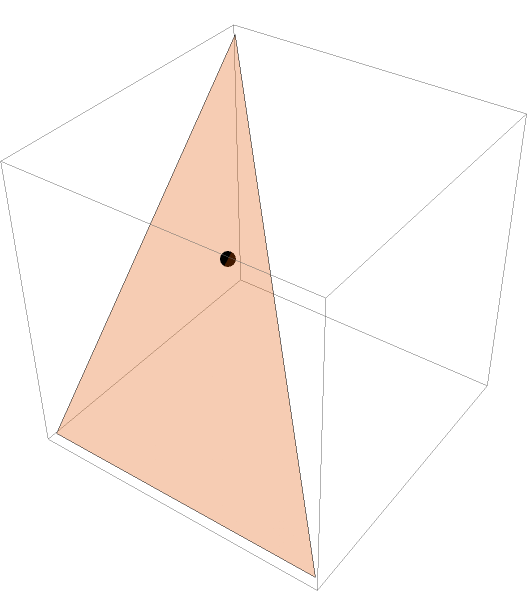 |
The Nagel point of the medial triangle is the same as the incenter of the reference triangle:
| In[5]:= | ![tri = {{0, 0}, {1.1, 4}, {5, 0}};
mtri = TriangleConstruct[tri, "MedialTriangle"];
na = ResourceFunction["NagelPoint"][mtri]](https://www.wolframcloud.com/obj/resourcesystem/images/46f/46f3a138-9a91-466a-874c-86b043303094/6ec1901dea882930.png) |
| Out[5]= |
| In[6]:= |
| Out[6]= |
| In[7]:= | ![Graphics[{
{Orange, Opacity[0.2], Triangle[tri]},
{Opacity[0.3, Blue], Disk[na[[1]], RegionDistance[Line[tri[[1 ;; 2]]], na[[1]]]]},
{Opacity[0.5, Red], mtri},
{
PointSize[
Scaled[0.08]],
Hue[0.58, 1, 1], na,
Text[
Style["Na", White, FontSize -> Scaled[0.04]],
Part[na, 1]]}
}] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/46f/46f3a138-9a91-466a-874c-86b043303094/38ba56313387bc3e.png) |
| Out[7]= | 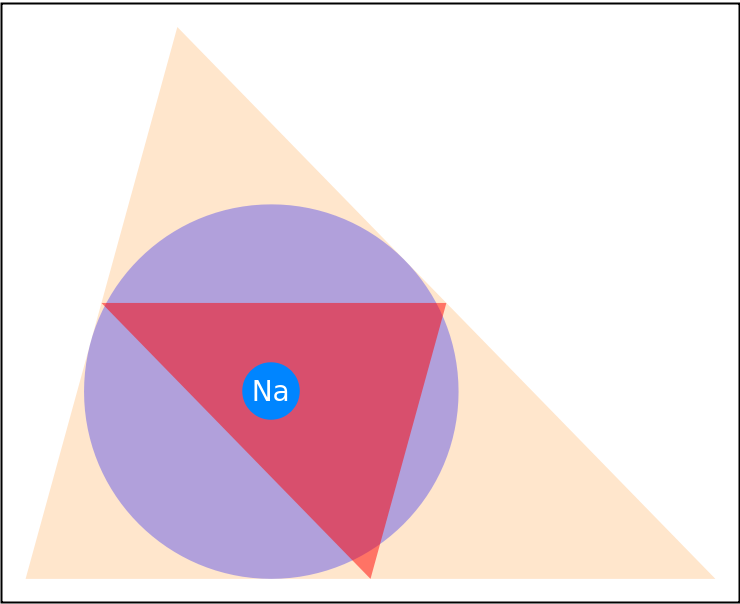 |
The Nagel point, the centroid and the incenter are collinear:

| In[8]:= |
| Out[8]= |
| In[9]:= | ![Graphics[{
{Dashed, InfiniteLine[{inc[[1]], na[[1]]}]},
{Orange, Opacity[0.2], Triangle[tri]},
MapThread[{
PointSize[
Scaled[0.08]],
Hue[0.58, 1, 1], #2,
Text[
Style[#, White, FontSize -> Scaled[0.04]],
Part[#2, 1]]}& , {{"G", "I", "Na"}, {cen, inc, na}}],
}] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/46f/46f3a138-9a91-466a-874c-86b043303094/3346c43722b3d5d7.png) |
| Out[9]= | 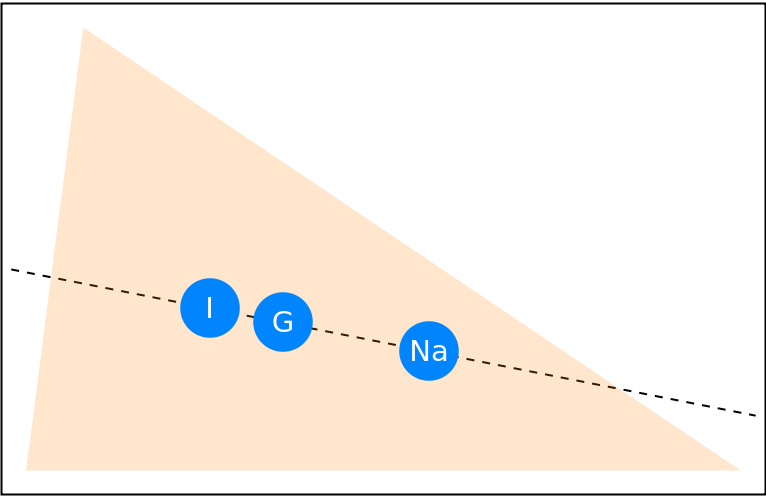 |
This work is licensed under a Creative Commons Attribution 4.0 International License