Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 InvoluteCurve

Source Notebook

Compute the involute of a curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["InvoluteCurve"][c,t]

computes the involute of a curve c with parameter t.

ResourceFunction["InvoluteCurve"][c,{t,tf}]

computes the involute by switching to numerical integration from 0 to tf.

Details

An involute can be constructed by moving the end of a taut cord unwound from the contour of a planar curve. The locus of points traced out by the end of the cord is called the involute. Tautness means the cord is always tangent to the curve from which it is unwound.

Examples

Basic Examples (2) 

Compute the involute of a circle:

In[1]:=
\[Alpha] = Entity["PlaneCurve", "Circle"]["ParametricEquations"][1][t]; invc = ResourceFunction["InvoluteCurve"][\[Alpha], t] // Simplify
Out[1]=

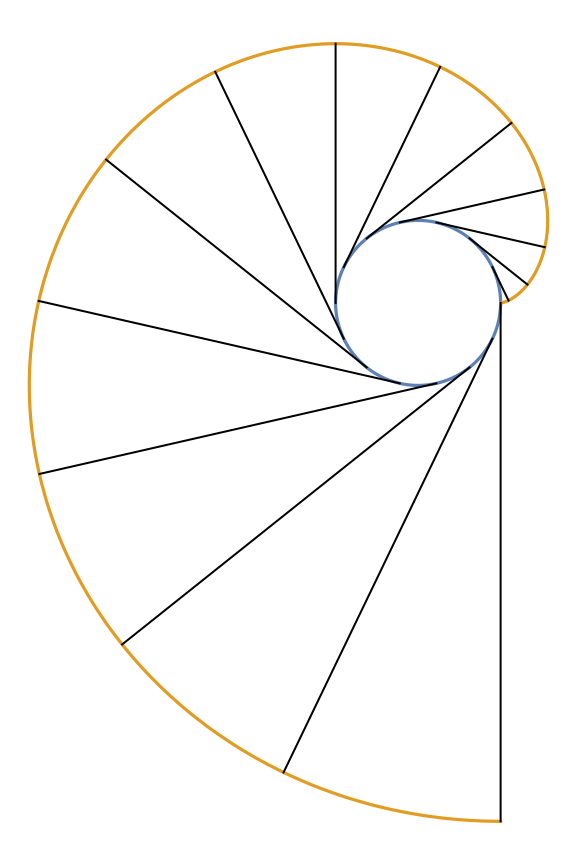
Plot the circle involute and tangent lines along the circle:

In[2]:=
z[k_] := Line[{\[Alpha], invc} /. t -> (\[Pi] k)/7] ParametricPlot[Evaluate[{\[Alpha], invc}], {t, 0, 2 \[Pi]}, Epilog -> Array[z, 14], Axes -> False]
Out[2]=

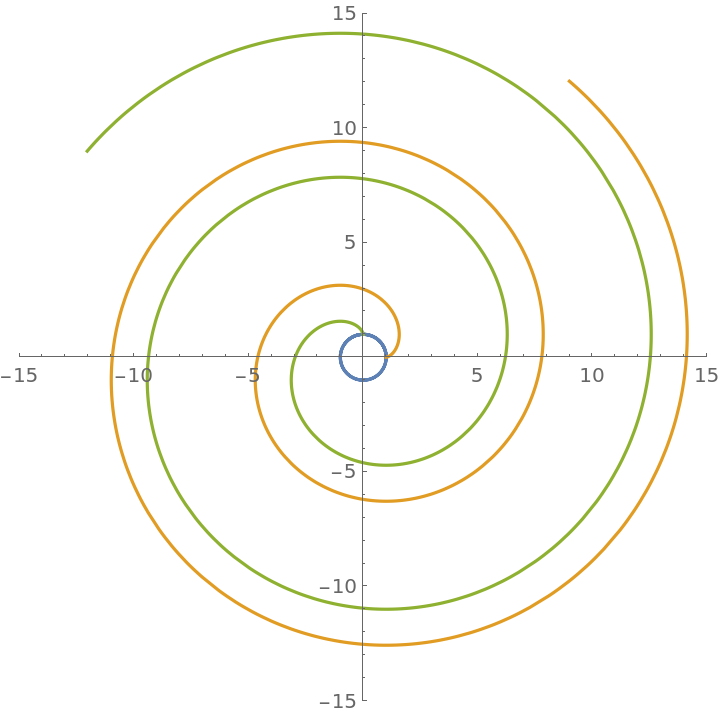
Start the involute at π/2:

In[3]:=
p = 15; ParametricPlot[ Evaluate[{\[Alpha], invc, ResourceFunction["InvoluteCurve"][\[Alpha] /. t -> t + \[Pi]/2, t]}], {t, 0, p}, PlotRange -> {{-p, p}, {-p, p}}]
Out[3]=

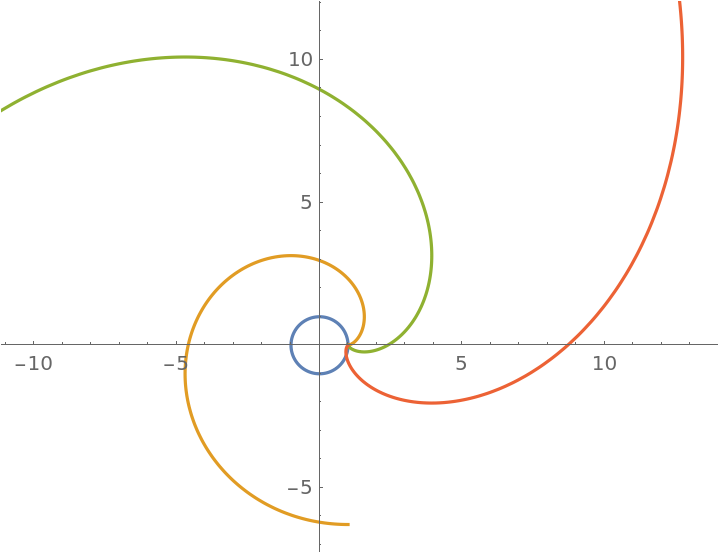
Nested involutes of the circle:

In[4]:=
ParametricPlot[ Evaluate[NestList[ ResourceFunction["InvoluteCurve"][#, t] &, \[Alpha], 3]], {t, 0.01, 2 \[Pi]}]
Out[4]=

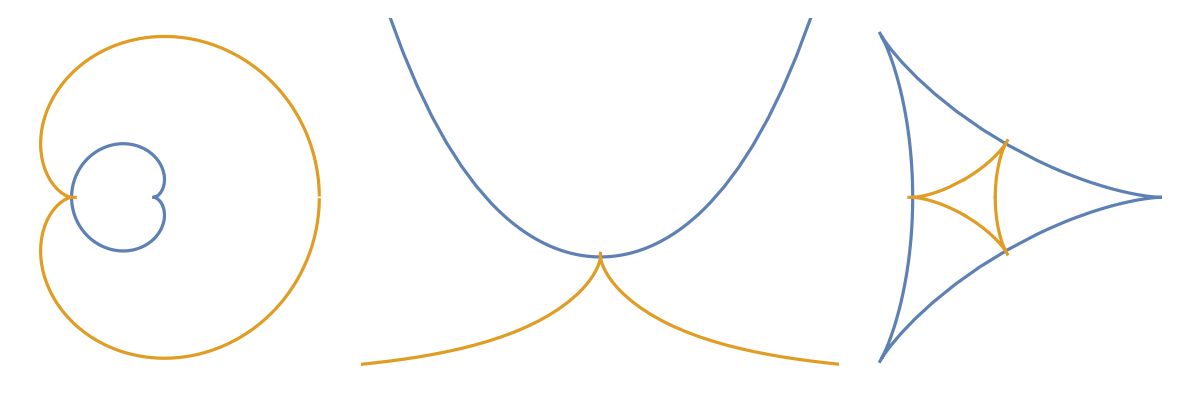
Here are some involute plots for several named curves:

In[5]:=
InvoluteCurvePlot[c_, {t_, t0_, tf_}, opts___] := ParametricPlot[ Evaluate[{c, ResourceFunction["InvoluteCurve"][c, t]}], {t, t0, tf}, opts, Axes -> False]; GraphicsRow[{InvoluteCurvePlot[ Entity["PlaneCurve", "Cardioid"]["ParametricEquations"][1][t], {t, 0.01, 2 \[Pi] - .01}], InvoluteCurvePlot[ Entity["PlaneCurve", "Catenary"]["ParametricEquations"][1][ t], {t, -3, 3}, PlotRange -> {{-2, 2}, {0, 3}}], InvoluteCurvePlot[ Entity["PlaneCurve", "Deltoid"]["ParametricEquations"][1][t], {t, 0.01, 2 \[Pi] - .01}]}]
Out[5]=

Properties and Relations (1) 

The evolute of a curve's involute is the curve itself:

In[6]:=
ResourceFunction["EvoluteCurve"][ ResourceFunction["InvoluteCurve"][{f[t], g[t]}, t], t] // FullSimplify
Out[6]=

Possible Issues (4) 

The eight curve:

In[7]:=
eight[t_] := {Sin[t], Sin[t] Cos[t]}

The involute curve:

In[8]:=
f = ResourceFunction["InvoluteCurve"][eight[t], t]
Out[8]=

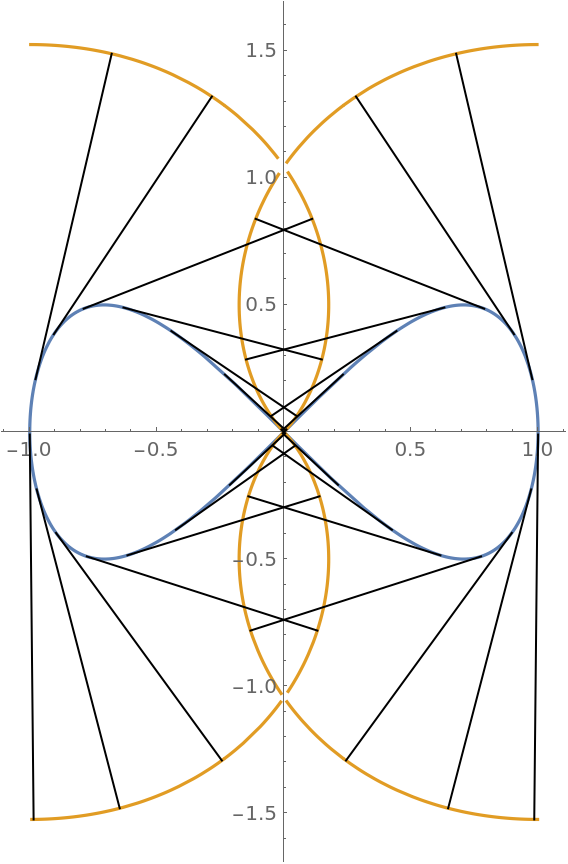
The involute curve using the expression shown above gives the same result four times:

In[9]:=
z1[k_] := Line[{eight[t], ResourceFunction["InvoluteCurve"][eight[t], t]} /. t -> (\[Pi] k)/14 + .01] ParametricPlot[Evaluate[{eight[t], f}], {t, 0.01, 2 \[Pi] - .01}, Epilog -> Array[z1, 28]]
Out[9]=

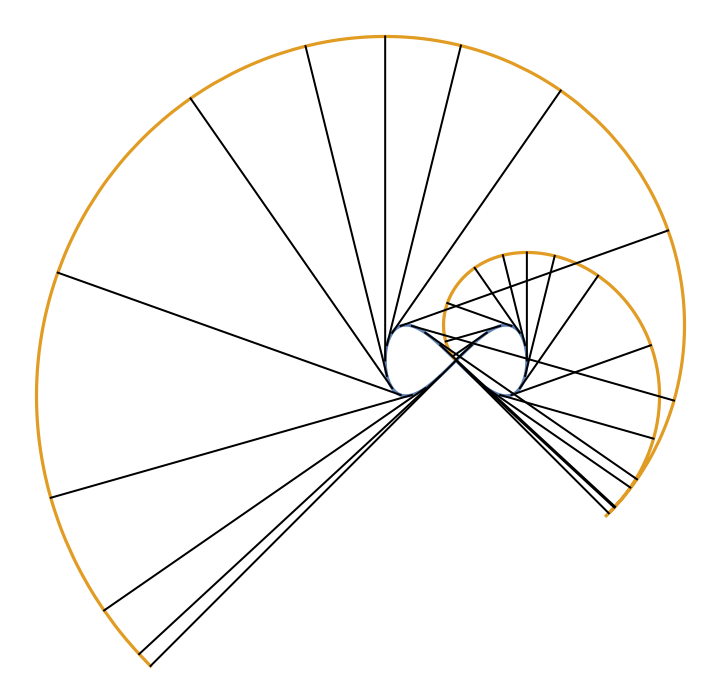
Using numerical integration gives the correct result:

In[10]:=
z[k_] := Line[{eight[tf], ResourceFunction["InvoluteCurve"][ eight[tf], {tf, (\[Pi] k)/14}]} /. tf -> (\[Pi] k)/14] ParametricPlot[{eight[tf], ResourceFunction["InvoluteCurve"][eight[t], {t, tf}] /. t -> tf}, {tf, 0.01, 2 \[Pi]}, Epilog -> Array[z, 28], Axes -> False]
Out[10]=

Publisher

Enrique Zeleny

Version History

  • 1.1.0 – 29 March 2021
  • 1.0.0 – 16 March 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information