Function Repository Resource:

FindEquationalPath (1.0.0) current version: 1.0.1 »

Find a path that goes from one expression to another with a sequence of replacements

Contributed by: Nikolay Murzin

ResourceFunction["FindEquationalPath"][theorem, axioms]

finds a replacement path from the left-hand side of a theorem to its right-hand side using replacements specified by axioms.

ResourceFunction["FindEquationalPath"][proof]

find a path for the precomputed ProofObject proof.

ResourceFunction["FindEquationalPath"][…, hypothesis]

specify an explicit hypothesis lemma from the underlying ProofObject to return a path for.

ResourceFunction["FindEquationalPath"][…,hypothesis,conclusion]

specify an explicit conclusion lemma from the underlying ProofObject to be used in path construction.

ResourceFunction["FindEquationalPath"][…,prop]

returns a specified property prop of a replacement path.

Details and Options

ResourceFunction["FindEquationalPath"] uses FindEquationalProof to find a proof of equational proposition and by using cut-elimination, derives a sequential path of one-step replacements from one side of a theorem to another.

The replacement path consists of pattern expressions corresponding to logic formulas with patterns (like a Blank, a_) representing universal variables (ForAll) and other symbols representing functional constants (Exists).

Properties prop supported by ResourceFunction["FindEquationalPath"] include:

"ProofObject"

the corresponding ProofObject

"Path"

a list of expressions comprising a found path (default)

"Justification"

a list of axioms used in each subsequent step of a path together with its orientation and position

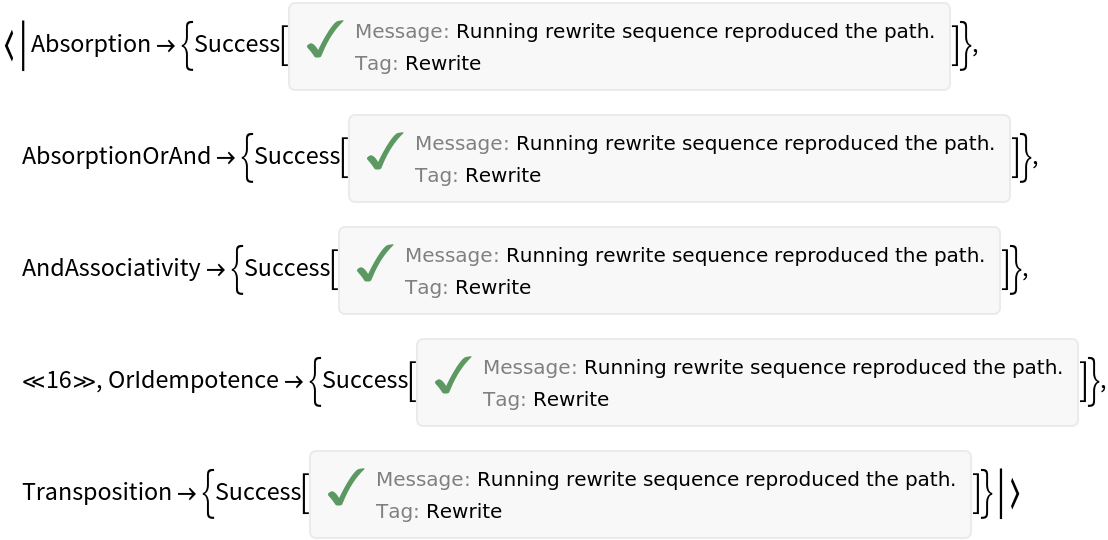
"Rewrites"

a list of rewriting functions that reproduce a path

"RewritesTest"

test rewriting functions to successfully reproduce a path

All

all of the above as an association

For the "Justification" property, axiom orientation is a direction of a corresponding rule, for example a==b can be used as a → b (right orientation) or b → a (left orientation).

Position of a step is a position of a subexpression at which a rule corresponding to an axiom is being applied.

Explicit hypothesis and conclusion lemmas are keys from the "Proof" or "ProofDataset" properties of a ProofObject, with {"Hypothesis", 1} and corresponding {"Conclusion", 1} being the default.

Explicit conclusion lemma is rarely needed, it is used as a starting point to generate a path by backtracking through a proof graph.

ResourceFunction["FindEquationalPath"] takes the option "Reverse". With "Reverse"→True, a reversed replacement path is returned.

Examples

Basic Examples (3)

Find a replacement path given a set of equations:

In[1]:=

Out[1]=

Find a replacement path using universally quantified equations:

In[2]:=

ResourceFunction["FindEquationalPath"][
ForAll[{x, y}, plus[x, plus[y, 0]] == plus[x, plus[0, y]]], {ForAll[x, plus[x, 0] == x], ForAll[x, plus[x, neg[x]] == 0], ForAll[{x, y, z}, plus[plus[x, y], z] == plus[x, plus[y, z]]]}]

Out[2]=

Find a much more complicated path:

In[3]:=

ResourceFunction["FindEquationalPath"][
ForAll[{a, b}, or[not[or[not[a], b]], not[or[not[a], not[b]]]] == a], {ForAll[{a, b}, and[a, b] == and[b, a]], ForAll[{a, b}, or[a, b] == or[b, a]], ForAll[{a, b}, and[a, or[b, not[b]]] == a], ForAll[{a, b}, or[a, and[b, not[b]]] == a], ForAll[{a, b, c}, and[a, or[b, c]] == or[and[a, b], and[a, c]]], ForAll[{a, b, c}, or[a, and[b, c]] == and[or[a, b], or[a, c]]]}] // Short

Out[3]=

Scope (7)

Use names from the AxiomaticTheory for a list of axioms and its notable theorems:

In[4]:=

Out[4]=

Specify a custom theorem with AxiomaticTheory axioms:

In[5]:=

$ResourceFunction["FindEquationalPath", ResourceVersion->"1.0.0"][((a\[CircleTimes]b)\[CircleTimes]c)\[CircleTimes] \!$\*OverscriptBox[\(a\[CircleTimes]c$, $_$]\) == b, "AbelianGroupAxioms"]$

Out[5]=

Use a ProofObject to find a replacement path:

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Specify a lemma or a different hypothesis from a proof to construct a path for:

In[8]:=

Out[8]=

In[9]:=

Out[9]=

Find a replacement path in a string substitution system:

In[10]:=

Out[10]=

In[11]:=

Out[11]=

Find a replacement path in a Wolfram model system:

In[12]:=

Out[12]=

In[13]:=

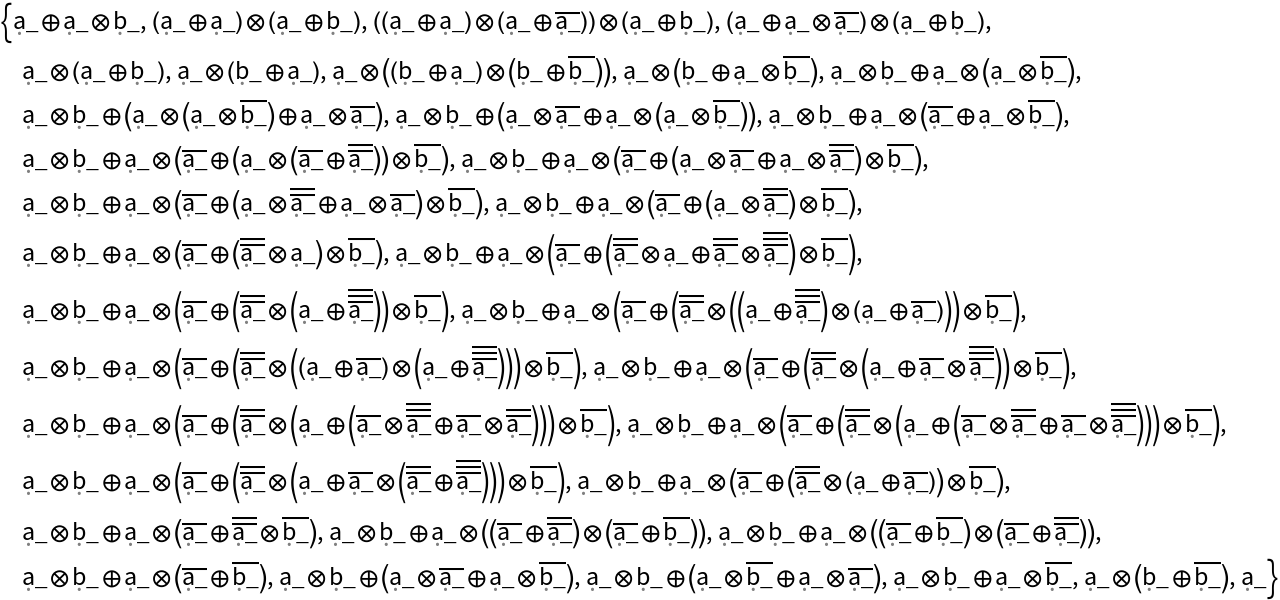
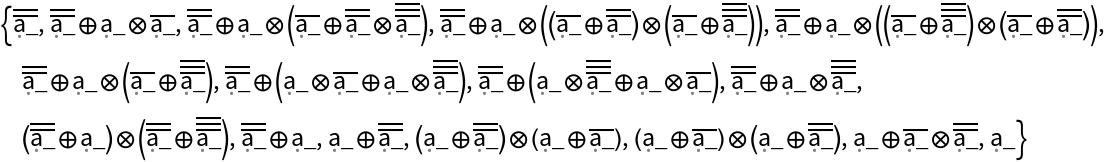
ResourceFunction["WolframModelPlot"][#, VertexLabels -> Automatic] & /@
Reverse[
First /@ Gather[Sort /@ (List /@ ResourceFunction["FindEquationalPath"][
proof] /. {CircleMinus | CirclePlus | CircleTimes -> List, CircleDot -> Sequence})]
]

Out[13]=

Reproduce the replacement path using rewriting functions:

In[14]:=

In[15]:=

$FoldList[#2[#1] &, \[FormalA]_\[CircleTimes](\[FormalA]_\[CirclePlus]\[FormalB]_), rewrites]$

Out[15]=

Options (1)

Reverse (1)

Reverse a path:

In[16]:=

Out[16]=

Neat Examples (3)

Find a replacement path for a well known syllogism by specifying an existentially quantified goal:

In[17]:=

$ResourceFunction["FindEquationalPath"][\!$ \*SubscriptBox[\(\[Exists]$, $x$]$Mortal[x]$\), {\!$ \*SubscriptBox[\(\[ForAll]$, $x$]$(Man[x] \[Implies] Mortal[x])$\), \!$ \*SubscriptBox[\(\[Exists]$, $x$]$Man[x]$\)}, "Reverse" -> True] /. {p_ \!$\* TagBox["||", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"||"]$ \!$\* TagBox["!", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!"]$ p_ :> True, \!$\* TagBox["!", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!"]$ p_ \!$\* TagBox["||", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"||"]$ q_ :> p \!$\* TagBox["\[Implies]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Implies]"]$ q} // Column$

Out[17]=

Test Boolean theorems:

In[18]:=

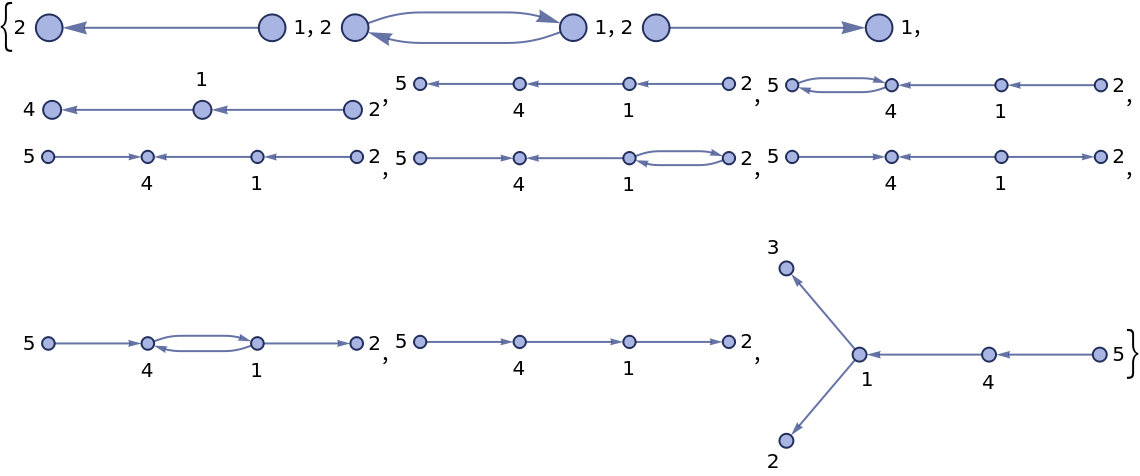
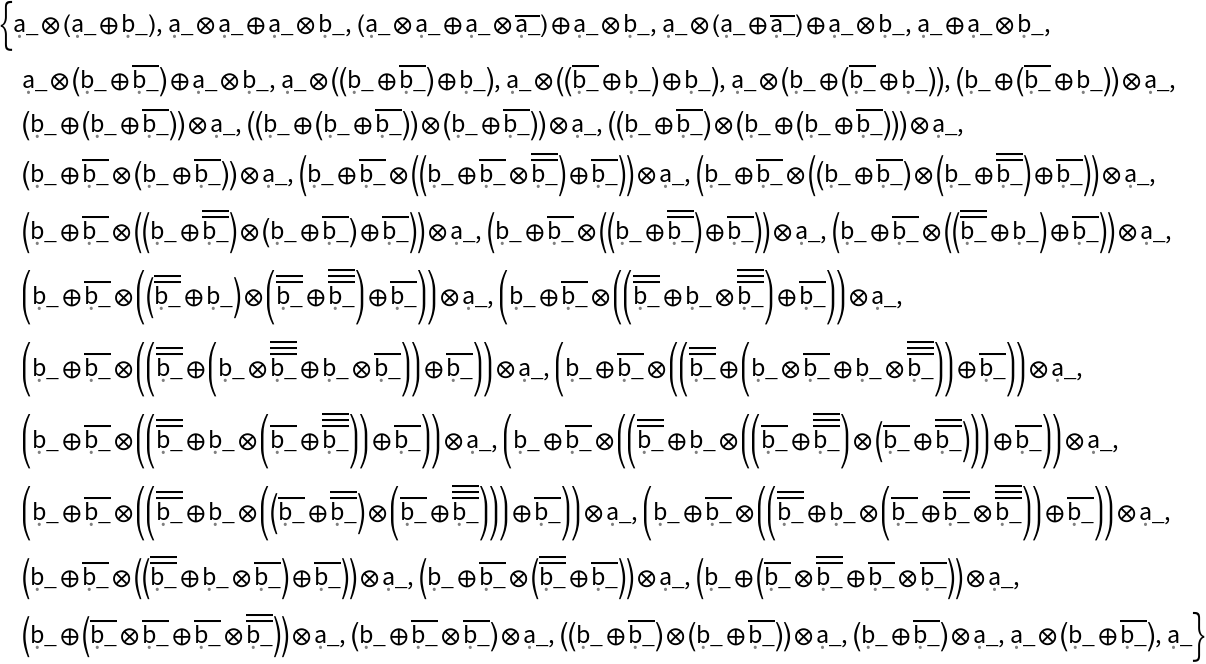
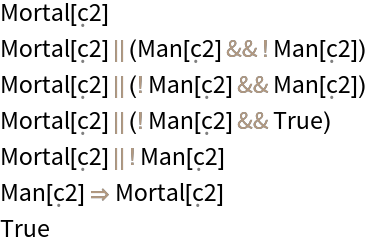
AssociationMap[
ResourceFunction["FindEquationalPath"][#, "BooleanAxioms", All][
"RewriteTest"] & /@ AxiomaticTheory["BooleanAxioms", "NotableTheorems"][#] &, Keys@AxiomaticTheory["BooleanAxioms", "NotableTheorems"]] // Short

Out[18]=

An example from A New Kind of Science (p. 775):

In[19]:=

$proof = FindEquationalProof[p\[CenterDot]q == q\[CenterDot]p, {\!$ \*SubscriptBox[\(\[ForAll]$, $\[FormalA]$]$\((\[FormalA]\[CenterDot]\[FormalA])$\[CenterDot]$(\[FormalA]\[CenterDot]\[FormalA])$\)\) \[Implies] \[FormalA], \!$ \*SubscriptBox[\(\[ForAll]$, ${\[FormalA], \[FormalB]}$]$\[FormalA] == \((\[FormalA]\[CenterDot]\[FormalA])$\[CenterDot]$(\[FormalA]\[CenterDot]\[FormalB])$\)\), \!$ \*SubscriptBox[\(\[ForAll]$, ${\[FormalA], \[FormalB]}$]$\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalB])$ == \[FormalA]\[CenterDot]$(\[FormalB]\[CenterDot]\[FormalB])$\)\), \!$ \*SubscriptBox[\(\[ForAll]$, ${\[FormalA], \[FormalB], \[FormalC]}$]$\((\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\((\[FormalB]\[CenterDot]\[FormalC])$)\))\) == $(\[FormalB]\[CenterDot]\((\[FormalB]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalC])$)\))\)\)\)}]$

Out[19]=

In[20]:=

Out[20]=

It is two steps shorter, but it uses a reverse of one axiom:

In[21]:=

Out[21]=

Prove the existential version of the same theorem using a proof by refutation:

In[22]:=

$ResourceFunction["FindEquationalPath"][ Exists[{p, q}, p\[CenterDot]q == q\[CenterDot]p], {\!$ \*SubscriptBox[\(\[ForAll]$, $\[FormalA]$]$\((\[FormalA]\[CenterDot]\[FormalA])$\[CenterDot]$(\[FormalA]\[CenterDot]\[FormalA])$\)\) \[Implies] \[FormalA], \!$ \*SubscriptBox[\(\[ForAll]$, ${\[FormalA], \[FormalB]}$]$\[FormalA] == \((\[FormalA]\[CenterDot]\[FormalA])$\[CenterDot]$(\[FormalA]\[CenterDot]\[FormalB])$\)\), \!$ \*SubscriptBox[\(\[ForAll]$, ${\[FormalA], \[FormalB]}$]$\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalB])$ == \[FormalA]\[CenterDot]$(\[FormalB]\[CenterDot]\[FormalB])$\)\), \!$ \*SubscriptBox[\(\[ForAll]$, ${\[FormalA], \[FormalB], \[FormalC]}$]$\((\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\((\[FormalB]\[CenterDot]\[FormalC])$)\))\) == $(\[FormalB]\[CenterDot]\((\[FormalB]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalC])$)\))\)\)\)}]$

Out[22]=

Version History

1.0.1 – 25 January 2023
1.0.0 – 20 January 2023

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License