Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FindEquationalPath

Source Notebook

Find a path that goes from one expression to another with a sequence of replacements

Contributed by: Nikolay Murzin

ResourceFunction["FindEquationalPath"][theorem, axioms]

finds a replacement path from the left-hand side of a theorem to its right-hand side using replacements specified by axioms.

ResourceFunction["FindEquationalPath"][proof]

find a path for the precomputed ProofObject proof.

ResourceFunction["FindEquationalPath"][…, hypothesis]

specify an explicit hypothesis lemma from the underlying ProofObject to return a path for.

ResourceFunction["FindEquationalPath"][…,hypothesis,conclusion]

specify an explicit conclusion lemma from the underlying ProofObject to be used in path construction.

ResourceFunction["FindEquationalPath"][…,prop]

returns a specified property prop of a replacement path.

Details and Options

ResourceFunction["FindEquationalPath"] uses FindEquationalProof to find a proof of equational proposition and by using cut-elimination, derives an unrolled sequential path of one-step replacements from one side of a theorem to another.
The replacement path consists of pattern expressions corresponding to logic formulas with patterns (like a Blank, a_) representing universal variables (ForAll) and other symbols representing functional constants (Exists).
Properties prop supported by ResourceFunction["FindEquationalPath"] include:
"ProofObject"the corresponding ProofObject
"Path"a list of expressions comprising a found path (default)
"Justification"a list of axioms used in each subsequent step of a path together with its orientation and position
"Rewrites"a list of rewriting functions that reproduce a path
"RewritesTest"test rewriting functions to successfully reproduce a path
"Rules"axiom rules used at each step
"Bindings"variable bindings for the rewrites
"Substitutions"variable bindings substituted into rules
Allall of the above as an association
For the "Justification" property, axiom orientation is a direction of a corresponding rule, for example a==b can be used as a → b (right orientation) or b → a (left orientation).
Position of a step is a position of a subexpression at which a rule corresponding to an axiom is being applied.
Explicit hypothesis and conclusion lemmas are keys from the "Proof" or "ProofDataset" properties of a ProofObject, with {"Hypothesis", 1} and corresponding {"Conclusion", 1} being the default.
Explicit conclusion lemma is rarely needed, it is used as a starting point to generate a path by backtracking through a proof graph.
ResourceFunction["FindEquationalPath"] takes the following options:
"Reverse"Falsereverse replacement path
"Simplify"Truesimplify path by removing sequences between identical expressions
"Canonicalize"Falseassign canonical names to variables
"TerminalLemmas"{}list of lemmas to terminate unrolling and shorten the path, effectively treating them as axioms

Examples

Basic Examples (3) 

Find a replacement path given a set of equations:

In[1]:=
ResourceFunction["FindEquationalPath"][a == d, a == b && b == c && c == d]
Out[1]=

Find a replacement path using universally quantified equations:

In[2]:=
ResourceFunction["FindEquationalPath"][ ForAll[{x, y}, plus[x, plus[y, 0]] == plus[x, plus[0, y]]], {ForAll[x, plus[x, 0] == x], ForAll[x, plus[x, neg[x]] == 0], ForAll[{x, y, z}, plus[plus[x, y], z] == plus[x, plus[y, z]]]}]
Out[2]=

Find a much more complicated path:

In[3]:=
ResourceFunction["FindEquationalPath"][ ForAll[{a, b}, or[not[or[not[a], b]], not[or[not[a], not[b]]]] == a], {ForAll[{a, b}, and[a, b] == and[b, a]], ForAll[{a, b}, or[a, b] == or[b, a]], ForAll[{a, b}, and[a, or[b, not[b]]] == a], ForAll[{a, b}, or[a, and[b, not[b]]] == a], ForAll[{a, b, c}, and[a, or[b, c]] == or[and[a, b], and[a, c]]], ForAll[{a, b, c}, or[a, and[b, c]] == and[or[a, b], or[a, c]]]}] // Short
Out[3]=

Scope (8) 

Use names from the AxiomaticTheory for a list of axioms and its notable theorems:

In[4]:=
ResourceFunction[ "FindEquationalPath"]["AbsorptionOrAnd", "BooleanAxioms"]
Out[4]=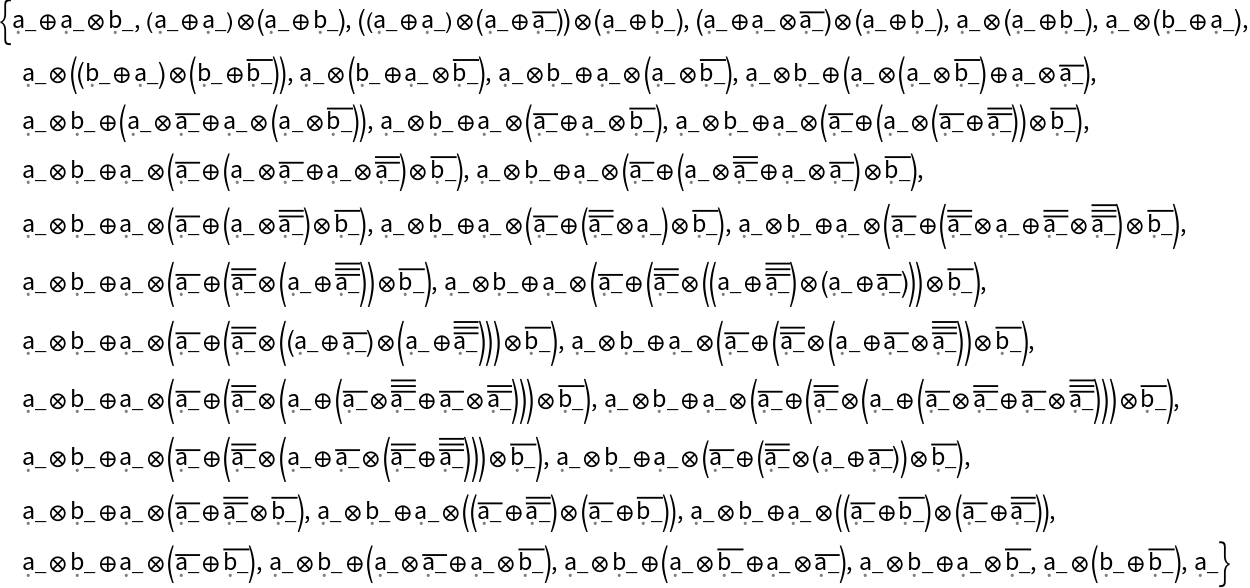

Specify a custom theorem using AxiomaticTheory axioms:

In[5]:=
ResourceFunction[ "FindEquationalPath"][((a\[CircleTimes]b)\[CircleTimes]c)\[CircleTimes] \!\(\*OverscriptBox[\(a\[CircleTimes]c\), \(_\)]\) == b, "AbelianGroupAxioms"]
Out[5]=

Use a ProofObject to find a replacement path:

In[6]:=
proof = FindEquationalProof["DoubleNegation", "BooleanAxioms"]
Out[6]=
In[7]:=
ResourceFunction["FindEquationalPath"][proof]
Out[7]=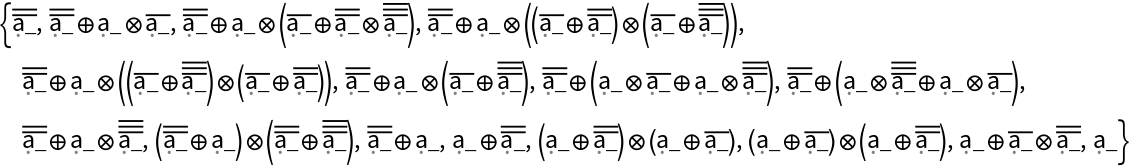

Specify a lemma or a different hypothesis from a proof to construct a path for:

In[8]:=
ResourceFunction[ "FindEquationalPath"]["DoubleNegation", "BooleanAxioms", {"CriticalPairLemma", 5}]
Out[8]=
In[9]:=
ResourceFunction["FindEquationalPath"]["DeMorgan", "BooleanAxioms", {"Hypothesis", 2}] // Short
Out[9]=

Find a replacement path in a string substitution system:

In[10]:=
proof = ResourceFunction["FindStringProof"][ "AAA" <-> "BBABAA", {"AA" <-> "BAA", "BAA" <-> "AB"}]
Out[10]=
In[11]:=
ResourceFunction["FindEquationalPath"][ proof] /. {c : A | B :> ToString[c], CircleDot -> StringJoin} // DeleteAdjacentDuplicates
Out[11]=

Find a replacement path in a Wolfram model system:

In[12]:=
proof = ResourceFunction[ "FindWolframModelProof"][{{1, 2}} <-> {{1, 2}, {1, 3}, {4, 1}, {5, 4}}, {{x, y}} <-> {{x, y}, {y, z}}]
Out[12]=
In[13]:=
ResourceFunction["WolframModelPlot"][#, VertexLabels -> Automatic] & /@ Reverse[ First /@ Gather[Sort /@ (List /@ ResourceFunction["FindEquationalPath"][ proof] /. {CircleMinus | CirclePlus | CircleTimes -> List, CircleDot -> Sequence})] ]
Out[13]=

Reproduce the replacement path using rewriting functions:

In[14]:=
rewrites = ResourceFunction["FindEquationalPath"]["DoubleNegation", "BooleanAxioms", "Rewrites"];
In[15]:=
ComposeList[rewrites, \!\(\*OverscriptBox[ OverscriptBox[\(p\), \(_\)], \(_\)]\)]
Out[15]=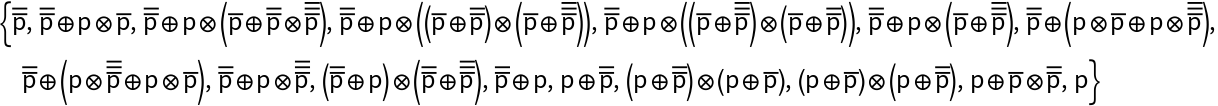

Return all properties of the path:

In[16]:=
pathData = ResourceFunction["FindEquationalPath"]["AndIdempotence", "BooleanAxioms", All, "Canonicalize" -> True]
Out[16]=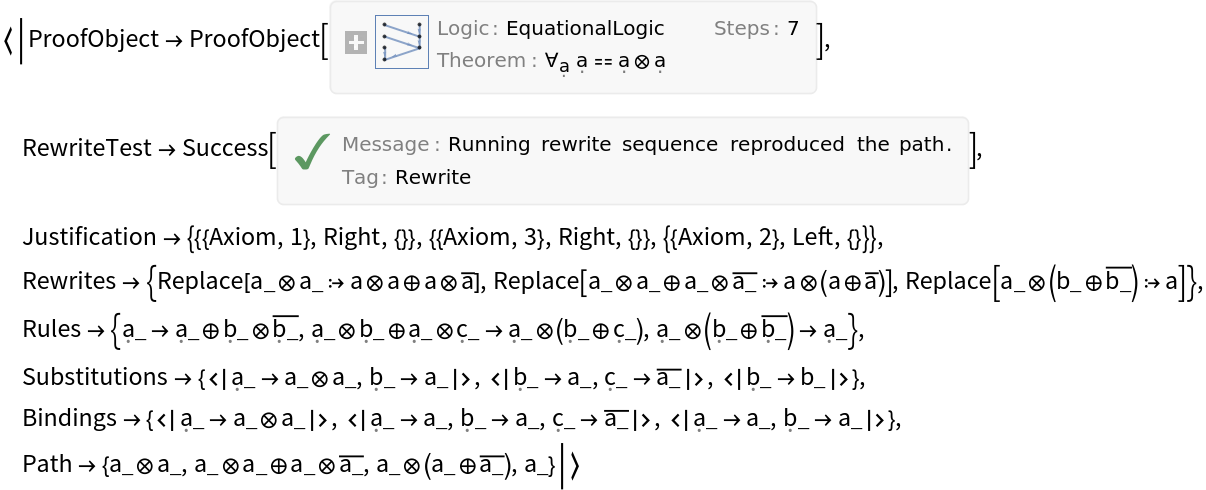

"Justification" is a list of axioms used in each subsequent step of a path together with its orientation and position:

In[17]:=
pathData["Justification"]
Out[17]=

"Rewrites" is a list of functions for ComposeList to reproduce the path:

In[18]:=
pathData["Rewrites"]
Out[18]=
In[19]:=
ComposeList[pathData["Rewrites"], a\[CircleTimes]a]
Out[19]=

"Rules" is a list of oriented lemma equations used at each step:

In[20]:=
pathData["Rules"]
Out[20]=

"Substitutions" is a list of additional variable replacements necessary to produce each intermediate term:

In[21]:=
pathData["Substitutions"]
Out[21]=

"Bindings" is a list of variable bindings of each rewriting step:

In[22]:=
pathData["Bindings"]
Out[22]=

Options (4) 

Reverse (1) 

Reverse a path:

In[23]:=
ResourceFunction["FindEquationalPath"][a == d, a == b && b == c && c == d, "Reverse" -> True]
Out[23]=

TerminalLemmas (1) 

Treat lemmas as axioms by terminating path unrolling and shorten the path:

In[24]:=
ResourceFunction["FindEquationalPath"][ FindEquationalProof["DoubleNegation", "BooleanAxioms"], "Justification"]
Out[24]=
In[25]:=
ResourceFunction["FindEquationalPath"][ FindEquationalProof["DoubleNegation", "BooleanAxioms"], "Justification", "TerminalLemmas" -> {{"SubstitutionLemma", 2}}]
Out[25]=

Simplify (1) 

Simplification of path is taking place by cutting path segments between identical elements:

In[26]:=
proof = FindEquationalProof["Commutativity", "WolframAxioms"];
In[27]:=
pathSimple = ResourceFunction["FindEquationalPath"][ proof, {"SubstitutionLemma", 11}];
In[28]:=
path = ResourceFunction["FindEquationalPath"][ proof, {"SubstitutionLemma", 11}, "Simplify" -> False];
In[29]:=
seqs = Flatten /@ SequenceAlignment[LeafCount /@ path, LeafCount /@ pathSimple];
In[30]:=
ListStepPlot[ MapAt[Callout[#, path[[62 + 16]], {{{90, 400}, Above}}, LeaderSize -> 150, LabelVisibility -> All] &, {3, 1}]@ MapAt[Callout[#, path[[62]], {{{50, 300}, Above}}, LeaderSize -> 100, LabelVisibility -> All] &, {2, 1}]@ Insert[#, #[[3, 1]], {2, -1}] &@Insert[#, #[[2, 1]], {1, -1}] &@ TakeList[MapIndexed[Append[#2, #1] &, Catenate[seqs]], Length /@ seqs], PlotStyle -> {RGBColor[0.24, 0.6, 0.8], Red, RGBColor[0.24, 0.6, 0.8] }]
Out[30]=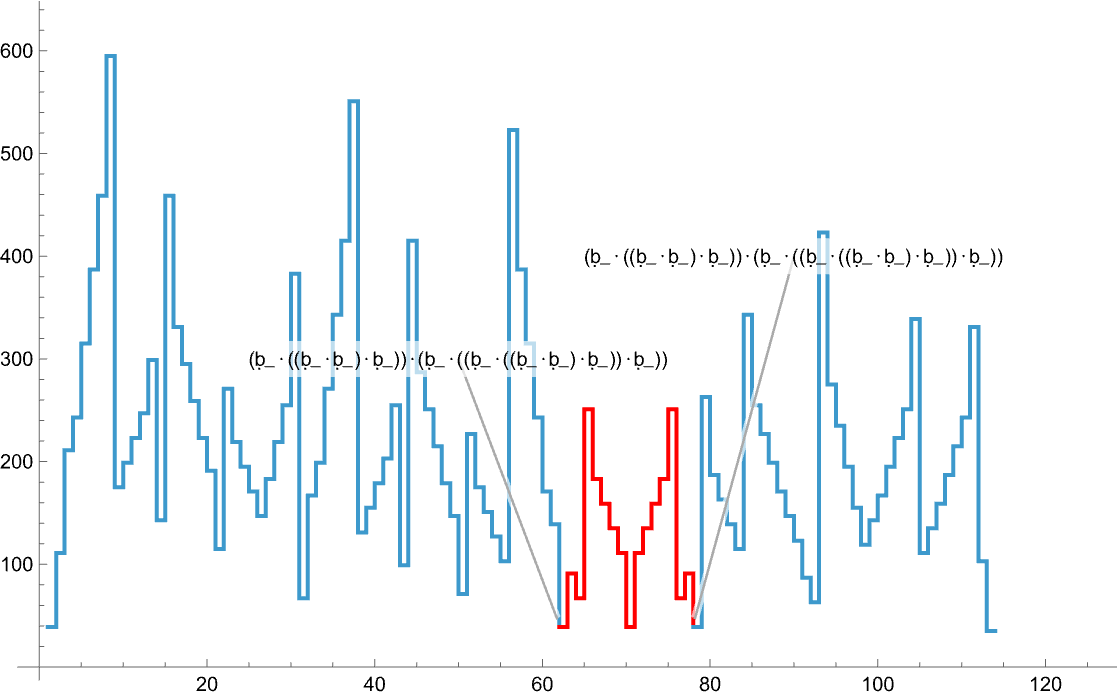

Canonicalize (1) 

Canonicalize variable names:

In[31]:=
ResourceFunction["FindEquationalPath"][ p == p\[CircleTimes](p\[CirclePlus]q), "BooleanAxioms", "Canonicalize" -> True]
Out[31]=

Neat Examples (4) 

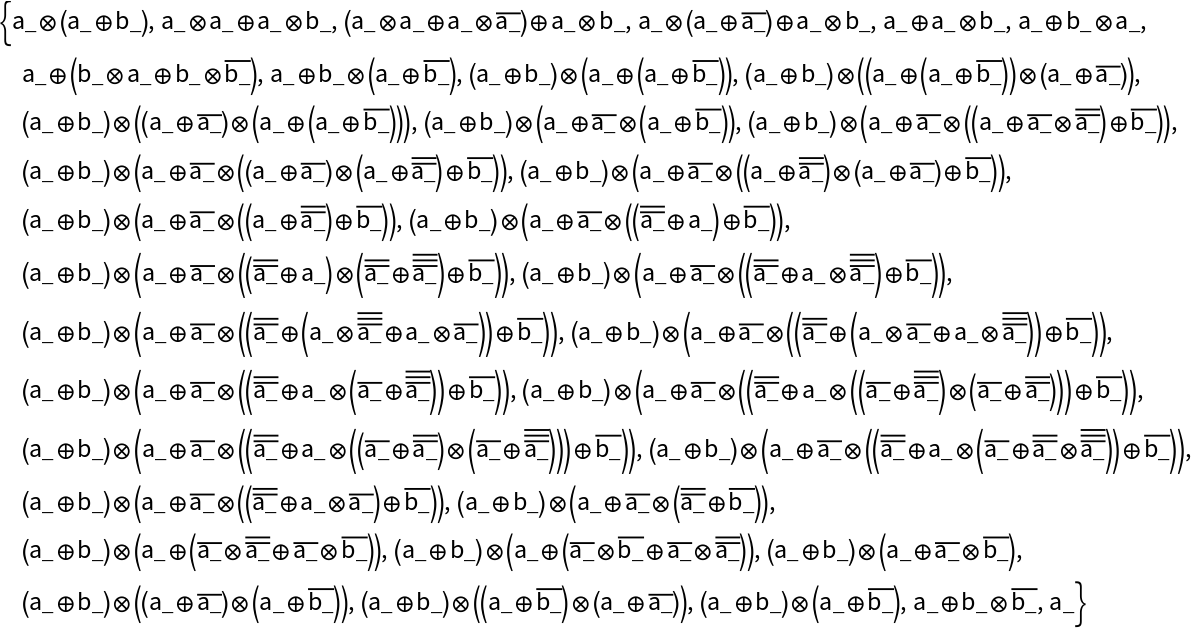Find a replacement path for a well known syllogism by specifying an existentially quantified goal:

In[32]:=
ResourceFunction["FindEquationalPath"][\!\( \*SubscriptBox[\(\[Exists]\), \(x\)]\(Mortal[x]\)\), {\!\( \*SubscriptBox[\(\[ForAll]\), \(x\)]\((Man[x] \[Implies] Mortal[x])\)\), \!\( \*SubscriptBox[\(\[Exists]\), \(x\)]\(Man[x]\)\)}, "Reverse" -> True] //. {\[FormalC]1 \!\(\* TagBox["||", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"||"]\) \!\(\* TagBox["!", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!"]\) \[FormalC]1 :> True, \[FormalC]2 -> "Socrates", \!\(\* TagBox["!", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!"]\) p_ \!\(\* TagBox["||", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"||"]\) q_ :> p \!\(\* TagBox["\[Implies]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Implies]"]\) q} // Column
Out[32]=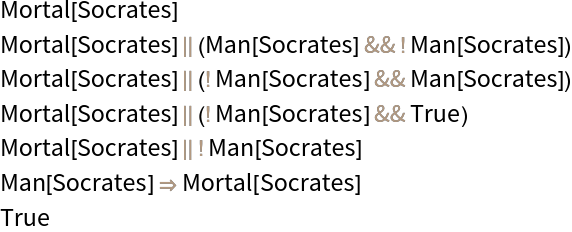

Test Boolean theorems:

In[33]:=
AssociationMap[ ResourceFunction["FindEquationalPath"][#, "BooleanAxioms", All][ "RewriteTest"] & /@ AxiomaticTheory["BooleanAxioms", "NotableTheorems"][#] &, Keys@AxiomaticTheory["BooleanAxioms", "NotableTheorems"]] // Short
Out[33]=

An example from A New Kind of Science (p. 775):

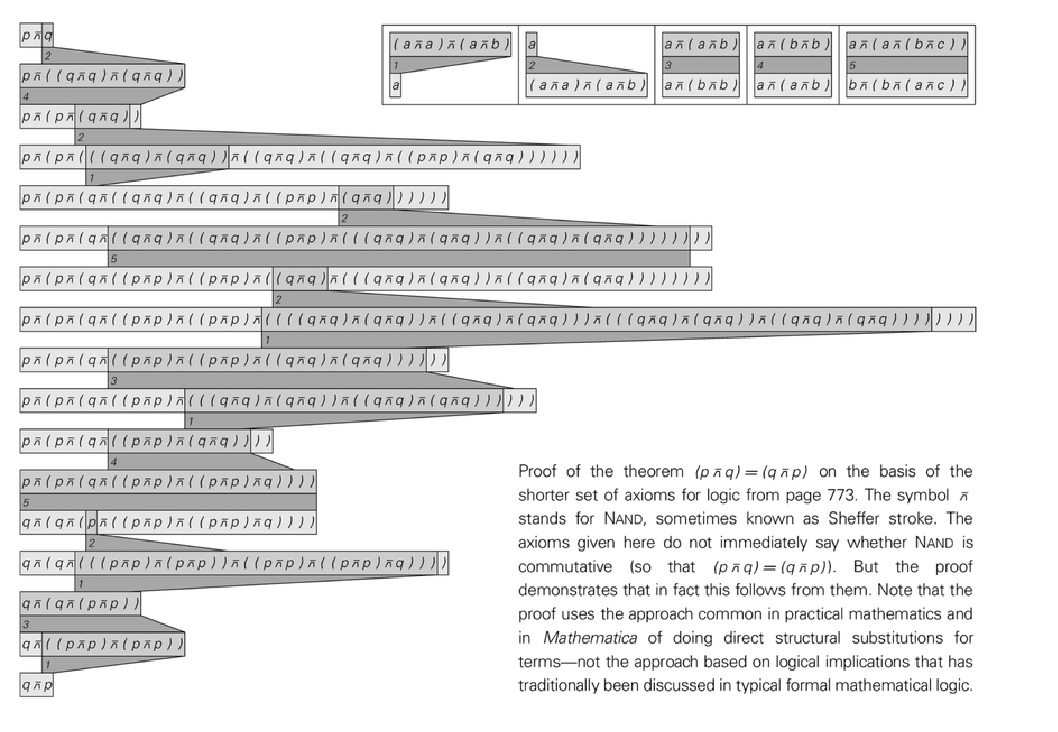
It is two steps shorter, but it uses a reverse of one axiom:

In[34]:=
Column[Style[#, 8] & /@ ResourceFunction["FindEquationalPath"][ ForAll[{p, q}, p\[CenterDot]q == q\[CenterDot]p], {\!\( \*SubscriptBox[\(\[ForAll]\), \(\[FormalA]\)]\(\((\[FormalA]\[CenterDot]\[FormalA])\)\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalA])\)\)\) \[Implies] \[FormalA], \!\( \*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB]}\)]\(\[FormalA] == \((\[FormalA]\[CenterDot]\[FormalA])\)\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalB])\)\)\), \!\( \*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB]}\)]\(\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalB])\) == \[FormalA]\[CenterDot]\((\[FormalB]\[CenterDot]\[FormalB])\)\)\), \!\( \*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB], \[FormalC]}\)]\(\((\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\((\[FormalB]\[CenterDot]\[FormalC])\))\))\) == \((\[FormalB]\[CenterDot]\((\[FormalB]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalC])\))\))\)\)\)}, "Path"] /. Verbatim[Pattern][x_, _] :> x, Frame -> All]
Out[34]=

Prove the existential version of the same theorem using a proof by refutation:

In[35]:=
ResourceFunction["FindEquationalPath"][ Exists[{p, q}, p\[CenterDot]q == q\[CenterDot]p], {\!\( \*SubscriptBox[\(\[ForAll]\), \(\[FormalA]\)]\(\((\[FormalA]\[CenterDot]\[FormalA])\)\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalA])\)\)\) \[Implies] \[FormalA], \!\( \*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB]}\)]\(\[FormalA] == \((\[FormalA]\[CenterDot]\[FormalA])\)\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalB])\)\)\), \!\( \*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB]}\)]\(\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalB])\) == \[FormalA]\[CenterDot]\((\[FormalB]\[CenterDot]\[FormalB])\)\)\), \!\( \*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB], \[FormalC]}\)]\(\((\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\((\[FormalB]\[CenterDot]\[FormalC])\))\))\) == \((\[FormalB]\[CenterDot]\((\[FormalB]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalC])\))\))\)\)\)}]
Out[35]=

Visualize a path with maximum extra details. Begin by defining visualization and utility functions:

In[36]:=
FramedParens[expr_, opts___] := If[LeafCount[expr, Heads -> False] > 1, RawBoxes[ FrameBox[ RowBox[{"(", ToBoxes[expr], ")"}], opts, ContentPadding -> False]], Framed[expr, opts, ContentPadding -> False]]
In[37]:=
Options[highlightExpression] = {"LeftLemmaFrame" -> {Background -> RGBColor[1, 0.85, 0.85]}, "RightLemmaFrame" -> {Background -> RGBColor[0.88, 1, 0.88]}, "InputFrame" -> {Background -> RGBColor[0.83, 0.88, 0.95]}, "OutputFrame" -> {Background -> RGBColor[0.67, 0.76, 0.91], FrameMargins -> 0}, "InputStyle" -> {}, "OutputStyle" -> {}}; highlightExpression[expr_, pos1_, pos2_, OptionsPattern[]] := If[ OrderedQ[{pos1, pos2}, LexicographicOrder], Reverse, #& ][ Composition[ If[pos2 === None, Identity, MapAt[If[pos2 === {}, Framed, FramedParens][ Style[#, OptionValue["OutputStyle"]], OptionValue["OutputFrame"], FrameStyle -> None, ContentPadding -> False]& , {pos2}]], If[pos1 === None, #& , MapAt[If[pos1 === {}, Framed, FramedParens][ Style[#, OptionValue["InputStyle"]], OptionValue["InputFrame"], FrameMargins -> 1, FrameStyle -> None, ContentPadding -> False]& , {pos1}]]]]@expr
In[38]:=
PatternsToSymbols[expr_] := expr /. Verbatim[Pattern][x_, _] :> x
In[39]:=
Options[visualizeRow] = Join[{"ShowTheorem" -> False, "ShowLemmas" -> False, "ShowBindings" -> False, "ShowSubstitutions" -> False, "LemmaStyle" -> {}, "LemmaFrame" -> {Background -> GrayLevel[0.9], FrameStyle -> GrayLevel[0.7]}}, Options[highlightExpression]]; visualizeRow[opts : OptionsPattern[]] := With[{showTheoremQ = TrueQ[ OptionValue["ShowTheorem"]], showLemmasQ = TrueQ[ OptionValue["ShowLemmas"]], showSubstitutions = If[ TrueQ[ OptionValue["ShowSubstitutions"]], Row[#, ","]& , Nothing& ], showBindings = If[ TrueQ[ OptionValue["ShowBindings"]], Row[ MapApply[Row[{#, ":", #2}]& , #], ","]& , Nothing& ], showLemmaLabel = Replace[{ Pattern[kind, Blank[]], Pattern[k, Blank[]]} :> Replace[ StringTake[kind, 1], "C" -> "B"] <> ToString[k]]}, Replace[{{ Pattern[tooltip, Blank[]], { Pattern[lemma, Blank[]], Blank[], None}, None, BlankNullSequence[]} :> { Tooltip[ Framed[ Style[ If[showTheoremQ, tooltip, showLemmaLabel[lemma]], OptionValue["LemmaStyle"]], OptionValue["LemmaFrame"]], If[showTheoremQ, showLemmaLabel[lemma], tooltip]], "", ""}, { Pattern[tooltip, Blank[]], {None, Blank[], Pattern[pos, Blank[]]}, Pattern[expr, Blank[]], None, Blank[], Pattern[subst, Blank[]]} :> { If[ TrueQ[ OptionValue["ShowSubstitutions"]], showSubstitutions[subst], SpanFromAbove], highlightExpression[expr, None, pos, FilterRules[{opts}, Options[highlightExpression]]], SpanFromAbove}, { Pattern[tooltip, Blank[]], { Pattern[lemma, Blank[]], None, None}, Pattern[expr, Blank[]], Pattern[prevPos, Blank[]], Pattern[bind, Blank[]], BlankNullSequence[]} :> { Tooltip[ Framed[ Style[ If[showTheoremQ, tooltip, showLemmaLabel[lemma]], OptionValue["LemmaStyle"]], OptionValue["LemmaFrame"]], If[showTheoremQ, showLemmaLabel[lemma], tooltip]], highlightExpression[expr, prevPos, None, FilterRules[{opts}, Options[highlightExpression]]], showBindings[bind]}, { Pattern[tooltip, Blank[]], { Pattern[lemma, Blank[]], Pattern[dir, Blank[]], Pattern[pos, Blank[]]}, Pattern[expr, Blank[]], Pattern[prevPos, Blank[]], Pattern[bind, Blank[]], BlankNullSequence[]} :> { Row[{"=", Tooltip[ Framed[ If[showLemmasQ, MapApply[Rule, Replace[dir, {Left -> (Reverse[#, {2}]& ), Right -> Identity}][ tooltip]], showLemmaLabel[lemma] <> Replace[ dir, {Left -> "\[LeftArrow]", Right -> "->"}]], Replace[dir, {Left -> OptionValue["LeftLemmaFrame"], Right -> OptionValue["RightLemmaFrame"]}], FrameStyle -> None], If[showLemmasQ, showLemmaLabel[lemma], tooltip]]}], highlightExpression[expr, prevPos, pos, FilterRules[{opts}, Options[highlightExpression]]], showBindings[bind]}, { Pattern[tooltip, Blank[]], None, Pattern[expr, Blank[]], Pattern[prevPos, Blank[]], BlankNullSequence[]} :> {SpanFromAbove, highlightExpression[expr, None, prevPos, FilterRules[{opts}, Options[highlightExpression]]], SpanFromAbove}}]];
In[40]:=
VisualizePath // ClearAll Options[VisualizePath] = Join[{"DoubleRows" -> False, "ShowOperators" -> True, "ShowLemmas" -> False, "Grid" -> {FrameStyle -> GrayLevel[0.7], Dividers -> {{True}, {{True}}}, Spacings -> {0.5, 0.6}}}, Options[visualizeRow]]; VisualizePath[po_ProofObject, lemmas_, target_, opts : OptionsPattern[]] := VisualizePath[ ResourceFunction["FindEquationalPath"][po, target, All, "TerminalLemmas" -> lemmas], target, opts ] VisualizePath[pathData_Association, target_, opts : OptionsPattern[]] := Block[{path, justification, substitutions, bindings, showOperatorsQ = If[ TrueQ[ OptionValue["ShowOperators"]], Identity, RightComposition[ToBoxes, ReplaceAll["\[CenterDot]" -> ""], RawBoxes]], showLemmasQ = TrueQ[ OptionValue["ShowLemmas"]], statements = Map[ ResourceFunction["UnformalizeSymbols"], Normal[ pathData["ProofObject"]["ProofDataset"][All, "Statement"]]]}, {path, justification, substitutions, bindings} = Lookup[ pathData, {"Path", "Justification", "Substitutions", "Bindings"}]; path = PatternsToSymbols[ path]; bindings = PatternsToSymbols[ Normal[bindings]]; substitutions = PatternsToSymbols[ Normal[substitutions]]; Grid[ MapThread[ RightComposition[List, ResourceFunction["UnformalizeSymbols"], visualizeRow[ FilterRules[{opts}, Options[visualizeRow]]]], If[ TrueQ[ OptionValue["DoubleRows"]], { Lookup[statements, Prepend[target][ Append[None][ Riffle[ Part[justification, All, 1], None]]]], Prepend[{target, None, None}][ Riffle[ ReplacePart[justification, { Blank[], 3} -> None], ReplacePart[justification, { Blank[], 1} -> None]]], Prepend[None][ Prepend[ First[path]][ Riffle[ Rest[path], Part[path, Span[2, -2]]]]], Prepend[None][ Append[None][ Riffle[ Part[justification, All, 3], None]]], Prepend[None][ Append[None][ Riffle[bindings, None]]], Prepend[None][ Prepend[None][ Riffle[substitutions, None]]]}, { Lookup[statements, Prepend[target][ Part[justification, All, 1]]], Prepend[{target, None, None}][justification], path, Append[None][ Part[justification, All, 3]], Prepend[{}][bindings], Prepend[<||>][substitutions]}]], OptionValue["Grid"], Frame -> True, Alignment -> {Left, Center}]]

Use All to get all the information for the path:

In[41]:=
pathData = ResourceFunction["FindEquationalPath"]["DoubleNegation", "BooleanAxioms", All, "Canonicalize" -> True];

Visualize it as a table:

In[42]:=
VisualizePath[ pathData, {"Hypothesis", 1}, "ShowSubstitutions" -> True, "ShowBindings" -> True, "DoubleRows" -> True, "ShowLemmas" -> True, "ShowTheorem" -> True, "Grid" -> {FrameStyle -> LightGray, Dividers -> {{True}, {False, {True, False}}}}]
Out[42]=

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.1.0 – 22 January 2025
  • 1.0.1 – 25 January 2023
  • 1.0.0 – 20 January 2023

Related Resources

Author Notes

1.1.0 change notes: - Add "TerminalLemmas", "Simplify" and "Canonicalize" options - Add "Rules", "Bindings" and "Substitutions" return properties

License Information