Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CubicSplineInterpolation

Source Notebook

Interpolate data with a cubic spline

Contributed by: Jan Mangaldan

ResourceFunction["CubicSplineInterpolation"][{f1,f2,…}]

constructs a cubic spline interpolation of the function values fi, assumed to correspond to x values 1, 2, ….

ResourceFunction["CubicSplineInterpolation"][{{x1,f1},{x2,f2},…}]

constructs a cubic spline interpolation of the function values fi corresponding to x values xi.

ResourceFunction["CubicSplineInterpolation"][data,cond]

uses conditions for the left and right endpoints specified by cond.

ResourceFunction["CubicSplineInterpolation"] returns an InterpolatingFunction object, which can be used like any other pure function.
The interpolation function returned by ResourceFunction["CubicSplineInterpolation"][data] is set up so as to agree with data at every point explicitly specified in data.
ResourceFunction["CubicSplineInterpolation"] yields an interpolant with continuous first and second derivatives.
The function values fi are expected to be real or complex numbers.
The function arguments xi must be real numbers.
ResourceFunction["CubicSplineInterpolation"][data] generates an InterpolatingFunction object that returns values with the same precision as those in data.
The following endpoint conditions can be specified for cond:
"NotAKnot"not-a-knot end condition
"Natural"natural end condition (zero second derivative)
"Clamped"set derivative at endpoint equal to the derivative of the polynomial passing through first (or last) four points
{"Clamped",d}set derivative at endpoint equal to d
{"Clamped",InterpolationOrder→m}set derivative at endpoint equal to the derivative of the polynomial passing through first (or last) m+1 points
"Second"set second derivative at endpoint equal to 0
{"Second",d}set second derivative at endpoint equal to d
{"Second",InterpolationOrder→m}set second derivative at endpoint equal to the second derivative of the polynomial passing through first (or last) m+1 points
"Periodic"periodic
ResourceFunction["CubicSplineInterpolation"][data] is equivalent to ResourceFunction["CubicSplineInterpolation"][data,"Periodic"] if the left and right endpoints of data have the same ordinate, and ResourceFunction["CubicSplineInterpolation"][data,"NotAKnot"] otherwise.
ResourceFunction["CubicSplineInterpolation"][data,{cond1,cond2}] uses cond1 for the left endpoint condition and cond2 for the right endpoint condition.

Examples

Basic Examples (3) 

Construct an approximate function that interpolates the data:

In[1]:=
f = ResourceFunction[ "CubicSplineInterpolation"][{0., 0.6, 1., 1.3, 1.4, 2.1}]
Out[1]=

Apply the function to find interpolated values:

In[2]:=
f[3.7]
Out[2]=

Plot the interpolation function along with the original data:

In[3]:=
Show[Plot[f[x], {x, 1, 6}], ListPlot[{0., 0.6, 1., 1.3, 1.4, 2.1}]]
Out[3]=

Interpolate between points at arbitrary x values:

In[4]:=
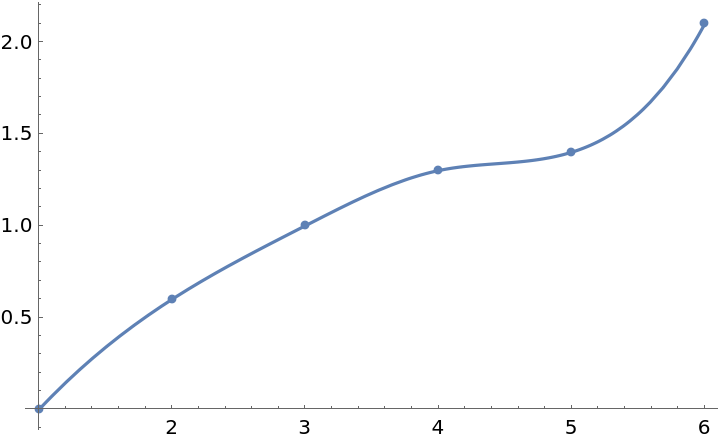
data = {{-1., -1.}, {-0.96, -0.4}, {-0.82, 0.3}, {-0.62, 0.75}, {0.13, 0.91}, {1., 1.}}; fun = ResourceFunction["CubicSplineInterpolation"][data]; Plot[fun[x], {x, -1, 1}, Epilog -> {Directive[AbsolutePointSize[5], ColorData[97, 4]], Point[data]}, PlotRange -> All]
Out[4]=

Plot a natural cubic spline:

In[5]:=
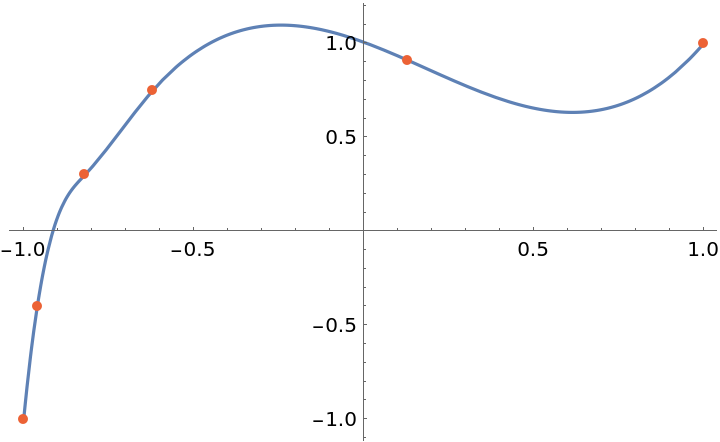
data = {{0., 0.}, {0.1, 0.3}, {0.5, 0.6}, {1., -0.2}, {2., 3.}}; fun = ResourceFunction["CubicSplineInterpolation"][data, "Natural"]; Plot[fun[x], {x, 0, 2}, Epilog -> {Directive[AbsolutePointSize[5], ColorData[97, 4]], Point[data]}, PlotRange -> All]
Out[5]=

Make a cubic spline with different left and right endpoint conditions:

In[6]:=
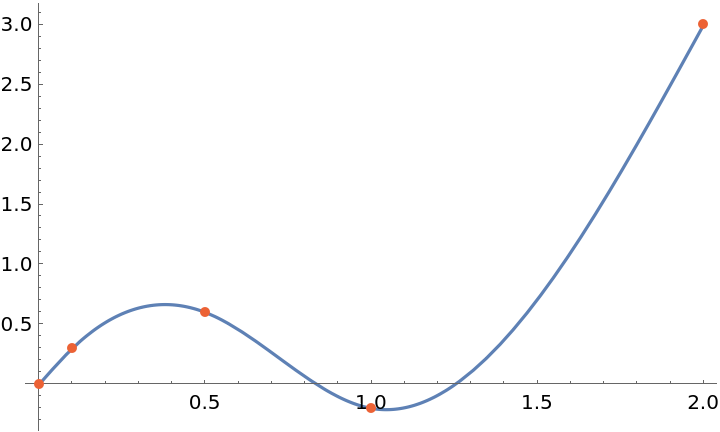
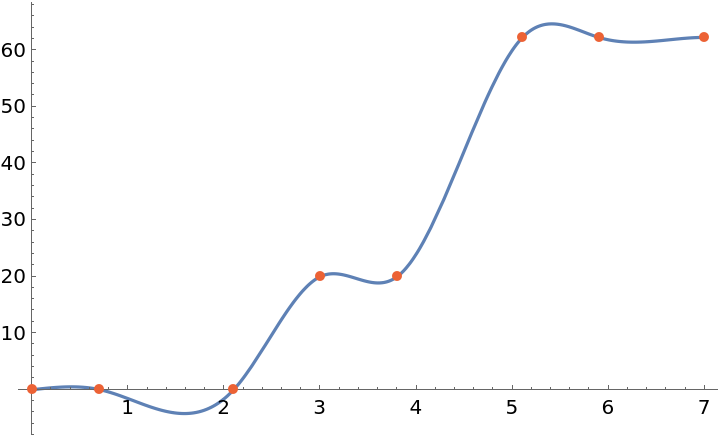
data = {{0., 0.}, {0.7, 0.02}, {2.1, 0.06}, {3., 20.}, {3.8, 20.}, {5.1, 62.2}, {5.9, 62.24}, {7., 62.26}}; fun = ResourceFunction["CubicSplineInterpolation"][ data, {{"Second", 0.1}, {"Clamped", InterpolationOrder -> 2}}]; Plot[fun[x], {x, 0, 7}, Epilog -> {Directive[AbsolutePointSize[5], ColorData[97, 4]], Point[data]}]
Out[6]=

Check that the second derivative at the left endpoint is reproduced:

In[7]:=
fun''[0]
Out[7]=

Form an interpolation from data given as a TimeSeries:

In[8]:=
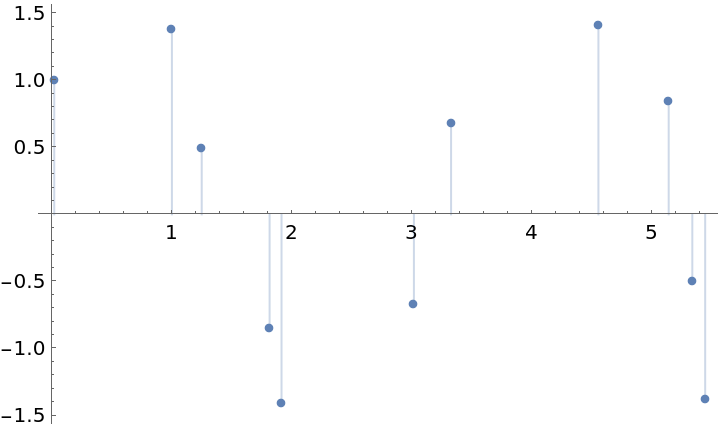
ts = TemporalData[ TimeSeries, {{{1, Cos[1] + Sin[1], Cos[2] + Sin[2], Cos[3] + Sin[3], Cos[4] + Sin[4], Cos[5] + Sin[5], Cos[6] + Sin[6], Cos[7] + Sin[7], Cos[8] + Sin[8], Cos[9] + Sin[9], Cos[10] + Sin[10]}}, {{{0.016965744360214943`, 0.9973865299845299, 1.24591736467102, 1.8114088692820352`, 1.9107450982712126`, 3.013995043949912, 3.323754146542503, 4.551557869716615, 5.13709169763333, 5.334143602077121, 5.441221219515277}}}, 1, {"Continuous", 1}, {"Discrete", 1}, 1, {ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}}, False, 10.1]; ListPlot[ts, Filling -> Axis]
Out[8]=
In[9]:=
fun = ResourceFunction["CubicSplineInterpolation"][ts]
Out[9]=
In[10]:=
Plot[fun[x], {x, ts["FirstTime"], ts["LastTime"]}]
Out[10]=

A periodic cubic spline:

In[11]:=
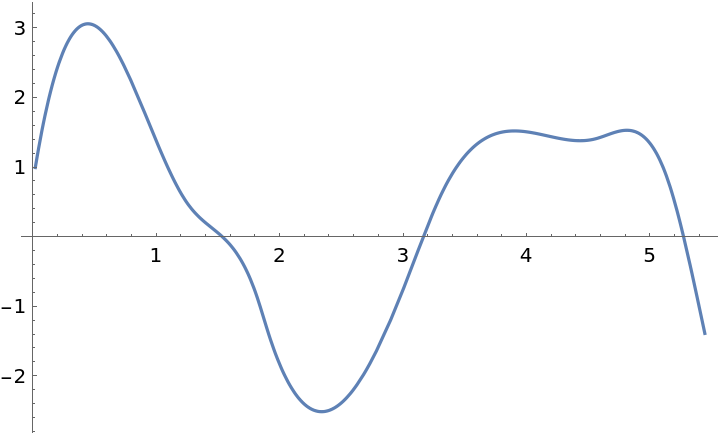
fun = ResourceFunction["CubicSplineInterpolation"][ RandomFunction[ BrownianBridgeProcess[{1, 1/2}, {5/2, 1/2}], {1, 5/2, 1/6}][ "Path"], "Periodic"]; Plot[fun[x], {x, -2, 4}]
Out[11]=

The interpolant returned by CubicMonotonicInterpolation is continuous up to its second derivative:

In[12]:=
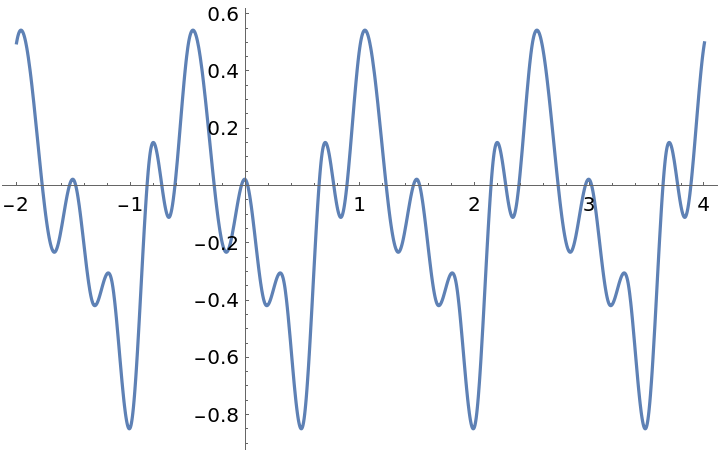
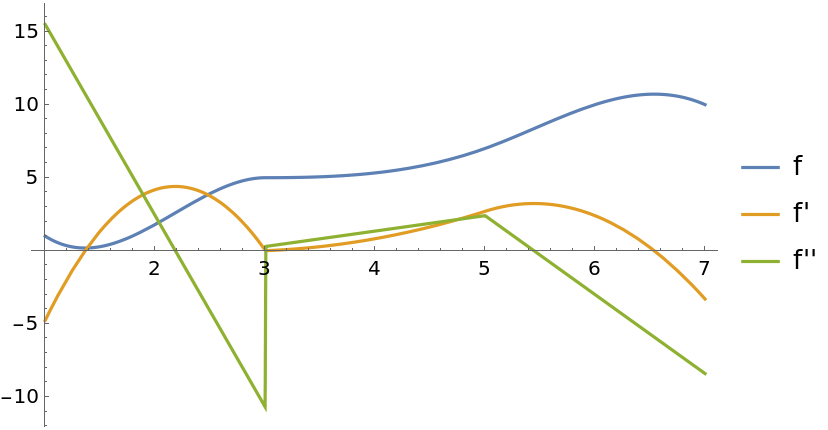
data = {{1., 1.}, {2., 1.8}, {3., 5.}, {3.006, 5.0001}, {5., 7.}, {6., 10.}, {7., 10.}}; fun = ResourceFunction["CubicSplineInterpolation"][data]; Plot[{fun[x], fun'[x], fun''[x]}, {x, 1, 7}, PlotLegends -> {"f", "f'", "f''"}, PlotRange -> All]
Out[12]=

Version History

  • 1.0.0 – 05 April 2021

Source Metadata

  • Citation:
    • de Boor C., A Practical Guide to Splines, Revised Edition. New York: Springer-Verlag, 2001.

Related Resources

License Information