Basic Examples (5)
Define local covariant base vectors in cylindrical coordinates:
Get covariant base vectors at point {r,ϕ,z}:
Define a mapping and coordinate system:
Calculate the associated covariant and contravariant base vectors:
Get normalized covariant and contravariant base vectors:
Verify their inverse relationships:
Get the covariant metric of mapping to a cylindrical system:
Compare the result with the cataloged named system of CoordinateChartData:
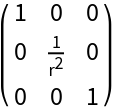
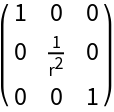
Do a similar computation to get the inverse metric:
Verify their inverse relationship:
Identify the volume factor of a mapping:
Compare with CoordinateChartData:
Calculate the covariant components of the Levi-Civita tensor  :
:
Get the contravariant components of the Levi-Civita tensor 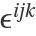 :
:
Find out which properties are available:
Scope (9)
Use the contravariant Levi-Civita symbol to evaluate the cross product 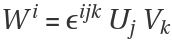 :
:
Check the above result by calculating the cross product of contravariant base vectors b3=b1⨯b2:
Affine coordinate transformation (1)
Find out the properties of an affine coordinate transformation:
Polar coordinate transformation (1)
Compute properties for polar coordinates:
Surfaces embedded in 3D Euclidean space (4)
Identify some metrics on the surface of a sphere:
Get the tangent space (represented by the covariant vectors):
Find out the corresponding area factor:
Calculate the 2x2 metric tensor:
Note that these components of the covariant metric tensor correspond to the coefficients of the so-called first fundamental form. Confirm this using the resource function FirstFundamentalFormCoefficients:
Generate some metrics of a torus surface:
Get the covariant vectors (corresponding to the tangent space):
Test the orthogonality of the tangent space:
Compute the unit normal using the resource function UnitNormal and compare with the associated cross product:
Determine the covariant metric tensor:
Define a heart surface and determine some properties:
Compute the Jacobian and covariant metric tensor of a surface of revolution of a general curve r(z):
Curve embedded in 2D Euclidean space (3)
Obtain the arc length of a general 2D curve:
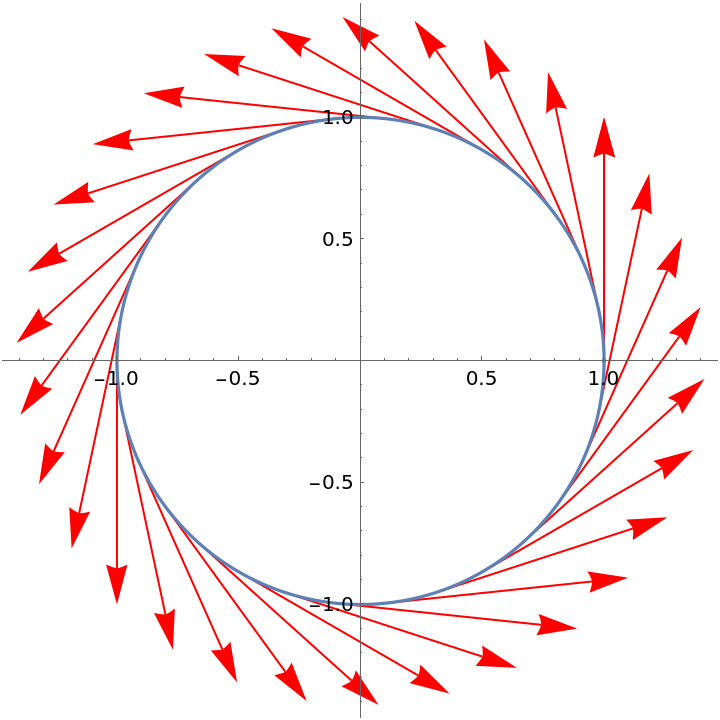
Compute the covariant vectors for a circle:
Visualize them using the resource function PlotVector:
Compute the circle's circumference:
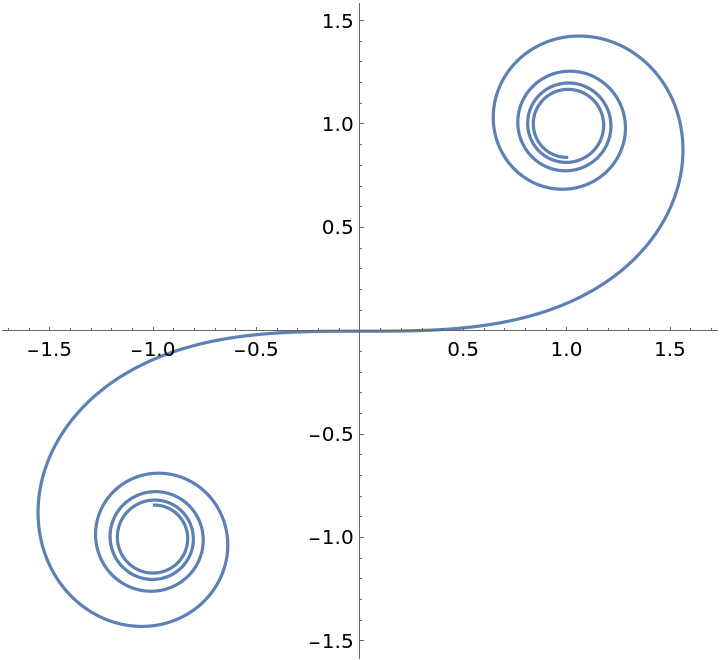
Plot a Cornu spiral and compute its length:
Options (4)
The option "UnitVectors" controls whether returned basis vectors are normalized. The default value is False:
Use "UnitVectors"→True to get normalized basis vectors:
Compute the surface area and volume of a generic torus through integration:
Compare, using named properties in cataloged surfaces here:
Compute the geodesic of a toroid:
Plot the geodesic curve:
Calculate the curve's length:
Define the normal vectors of a surface of revolution:
The inverse shift tensor 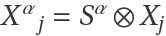 connects the surface space with the Euclidean ambient space:
connects the surface space with the Euclidean ambient space:
The normal space 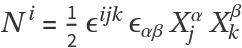 :
:
Plot normals of a random surface of revolution using the resource function PlotVector3D:
Properties and Relations (3)
The Jacobian matrix can be calculated with several Wolfram Language functions:
"MappingJacobian" and the transposition of "CovariantBaseVectors" represent the same property:
"InverseMappingJacobian" and "ContravariantBaseVectors" represent the same property as long as the mapping is between spaces of the same dimensionality:
Possible Issues (2)
For mappings to a manifold embedded in higher dimensional space, the properties "MappingJacobianDeterminant" and "InverseMappingJacobian" are not well-defined:
But "ContravariantBaseVectors" exists (so that, in this case, it is not the same as "InverseMappingJacobian"):
![ResourceFunction[
"CoordinateMappingData"][{Cos[#1[[2]]] #1[[1]], Sin[#1[[2]]] #1[[1]], #1[[3]]} &, "CovariantBaseVectors"]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/4e043f607c6581d9.png)
![ResourceFunction[
"CoordinateMappingData"][{Cos[#1[[2]]] #1[[1]], Sin[#1[[2]]] #1[[1]], #1[[3]]} &, "CovariantBaseVectors"][{r, \[Phi], z}]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/418eadba29ce8dfe.png)
![covBasisNormalized = ResourceFunction["CoordinateMappingData"][mapping, "CovariantBaseVectors", coords, "UnitVectors" -> True] // Simplify[#, {r > 0, \[Phi] > 0}] &](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/172f0a63d92cb2b3.png)
![conBasisNormalized = ResourceFunction["CoordinateMappingData"][mapping, "ContravariantBaseVectors", coords, "UnitVectors" -> True] // Simplify[#, {r > 0, \[Phi] > 0}] &](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/226e99f9e3a07676.png)
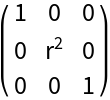
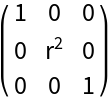
![]() :
:![]() :
:![]() :
:![wCon = ResourceFunction["CoordinateMappingData"][mapping, "LeviCivitaContravariant", coords] . {0, 1, 0} . {1, 0, 0} // Simplify[#, r > 0] &;
covBasis = ResourceFunction["CoordinateMappingData"][mapping, "CovariantBaseVectors", coords];
\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(3\)]\(wCon[[
i]] covBasis[[i]]\)\)](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/44d87d80669ebf3b.png)
![{conBasis, covBasis, invJacobian, conMetric, conLeviCivita, covLeviCivita, jacobian, jacobianDet, covMetric, volumefactor} = ResourceFunction["CoordinateMappingData"][mapping, #, coords] & /@ (ResourceFunction["CoordinateMappingData"][
"Properties"]);
MatrixForm /@ %](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/3f4f85cad8bf8307.png)

![mapping = {r Cos[\[Phi]], r Sin[\[Phi]]}; coords = {r, \[Phi]};
ResourceFunction["CoordinateMappingData"][mapping, #, coords] & /@ ResourceFunction["CoordinateMappingData"]["Properties"] // Simplify[#, r > 0] &](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/0e52484da0a50f56.png)

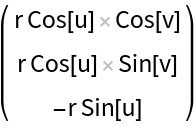
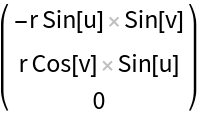
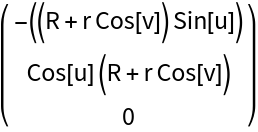
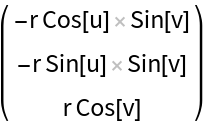
![heart = {Sin[s2] (15 Sin[s1] - 4 Sin[3 s1]), 8 Cos[s2], Sin[s2] (15 Cos[s1] - 5 Cos[2 s1] - 2 Cos[3 s1] - Cos[2 s1])};](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/02c8ad6d6554c88c.png)
![Show[{
ParametricPlot3D[heart, {s1, 0, 2 \[Pi]}, {s2, 0, \[Pi]}, PlotStyle -> Red, Mesh -> False],
ResourceFunction["PlotVector3D"][tangentSpace, heart, VectorStyle -> {{Thick, Blue}}]
}, Boxed -> False, Axes -> False, PlotRange -> All
] /. {s1 -> \[Pi]/5, s2 -> (2 \[Pi])/3}](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/4de5e22b61839a98.png)

![heartSurfaceArea = NIntegrate[
ResourceFunction["CoordinateMappingData"][heart, "VolumeFactor", {s1, s2}] // Simplify, {s1, 0, 2 \[Pi]}, {s2, 0, \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/74903aebf8a1280a.png)
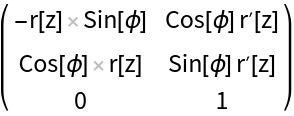
![Show[ResourceFunction["PlotVector"][
Table[(covBasis /. {r -> 1, t -> i}), {i, Range[0, 2 \[Pi], \[Pi]/15]}],
Table[({r Cos[t], r Sin[t]} /. {r -> 1, t -> i}), {i, Range[0, 2 \[Pi], \[Pi]/15]}], VectorStyle -> Red],
ParametricPlot[{r Cos[t], r Sin[t]} /. r -> 1, {t, 0, 2 \[Pi]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/4d2f02a3eba1a71d.png)
![\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-4\), \(4\)]\(\*
InterpretationBox[
TagBox[
DynamicModuleBox[{Typeset`open = False},
FrameBox[
PaneSelectorBox[{False->GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["CoordinateMappingData", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True->
DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"],
ImageSizeCache->{11., {1., 10.}}], False->
DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"],
ImageSizeCache->{11., {1., 10.}}]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{
{GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["CoordinateMappingData", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True->
DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False->
DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]},
{
StyleBox[
PaneBox[GridBox[{
{
RowBox[{
TagBox["\<\"Version (latest): \"\>",
"IconizedLabel"], " ",
TagBox["\<\"1.0.0\"\>",
"IconizedItem"]}]},
{
TagBox[
TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/81241af7-4081-4251-af9d-2dbfe85051d8/"},
"HyperlinkURL"],
"IconizedItem"]}
},
DefaultBaseStyle->"Column",
GridBoxAlignment->{"Columns" -> {{Left}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle",
FontFamily->"Roboto",
FontSize->11]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, {
GrayLevel[0.8]}, False}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open],
BaselinePosition->Baseline,
ImageSize->Automatic],
Background->RGBColor[
0.9686274509803922, 0.9764705882352941, 0.984313725490196],
BaselinePosition->Baseline,
DefaultBaseStyle->{},
FrameMargins->{{0, 0}, {1, 0}},
FrameStyle->RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627],
RoundingRadius->4]],
{"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"CoordinateMappingData"},
TagBoxNote->"FunctionResourceBox"],
ResourceFunction["CoordinateMappingData"],
BoxID -> "CoordinateMappingData",
Selectable->False][\(\(\*
TemplateBox[{"\"Cornu spiral\"",
RowBox[{"Entity", "[",
RowBox[{"\"PlaneCurve\"", ",", "\"CornuSpiral\""}], "]"}], "\"Entity[\\\"PlaneCurve\\\", \\\"CornuSpiral\\\"]\"", "\"plane curve\""},
"Entity"]["\<ParametricEquations\>"]\)[a]\)[
t], "\<VolumeFactor\>", {t}] \[DifferentialD]t\)\)](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/25cbc1eb953c1436.png)
![ResourceFunction[
"CoordinateMappingData"][{2 x + 2 y, 2 y, 2 z}, "CovariantBaseVectors", {x, y, z}, "UnitVectors" -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/29642a71e5333a1c.png)
![ResourceFunction[
"CoordinateMappingData"][{2 x + 2 y, 2 y, 2 z}, "CovariantBaseVectors", {x, y, z}, "UnitVectors" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/6759c6de89f84513.png)
![volumefactor = ResourceFunction[
"CoordinateMappingData"][{(R + r Cos[v]) Cos[
u], (R + r Cos[v]) Sin[u], r Sin[v]}, "VolumeFactor", {u, v}] //
Simplify[#, {r > 0, R + r Cos[v] > 0}] &;](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/19e56aa42148385c.png)
![t0 = 0; t1 = 208; (*curve paramters *)
geodesicParameters = Flatten@NDSolve[
ResourceFunction["Geodesic"][
Entity["Surface", "Torus"]["ParametricEquations"][1, 4][u, v], {u,
v}, t, {0, 0}, 89 Degree], {u, v}, {t, t0, t1}]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/053b11f9930e9d1b.png)
![Show[{ParametricPlot3D[
Evaluate[
Entity["Surface", "Torus"]["ParametricEquations"][1, 4][u, v]], {u, 0, 2 \[Pi]}, {v, 0, 2 \[Pi]}, PlotStyle -> Opacity[.5], Mesh -> False], ParametricPlot3D[geodesicCurve, {t, t0, t1}]}, Boxed -> False, Axes -> False, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/4ce09e59fd7e61f2.png)

![]() connects the surface space with the Euclidean ambient space:
connects the surface space with the Euclidean ambient space:![shiftInverseConCov = Table[
(ResourceFunction["CoordinateMappingData"][mapping, "ContravariantBaseVectors", coords][[\[Alpha]]]) .
(ResourceFunction["CoordinateMappingData"][{x1, x2, x3}, "CovariantBaseVectors", {x1, x2, x3}][[i]]),
{\[Alpha], 2}, {i, 3}] // Simplify;](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/54ea52cde232fc4e.png)
![]() :
:![(normalVector = (1/
2 (ResourceFunction[
"EinsteinSummation"][{{i, j, k}, {\[Alpha], \[Beta]}, {\[Alpha], j}, {\[Beta], k}}, {\[Epsilon]ijk, \[Epsilon]\[Alpha]\[Beta], x\[Alpha]j, x\[Beta]k}]) /.
{\[Epsilon]ijk -> ResourceFunction["CoordinateMappingData"][{x1, x2, x3}, "LeviCivitaContravariant", {x1, x2, x3}](*LeviCivitaTensor[
3]*),
\[Epsilon]\[Alpha]\[Beta] -> ResourceFunction["CoordinateMappingData"][mapping, "LeviCivitaCovariant", coords],
x\[Alpha]j -> shiftInverseConCov,
x\[Beta]k -> shiftInverseConCov} // Normal) // Simplify[#, {\[Phi] > 0, r[z] > 0}] &) // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/28cc27a27e24067f.png)
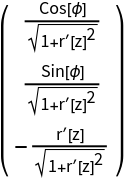
![SeedRandom[151];
n = 5;
list = Transpose[{Range[0, n - 1], RandomReal[{0.5, 2}, n]}];
ifun = Interpolation[list, InterpolationOrder -> 3];
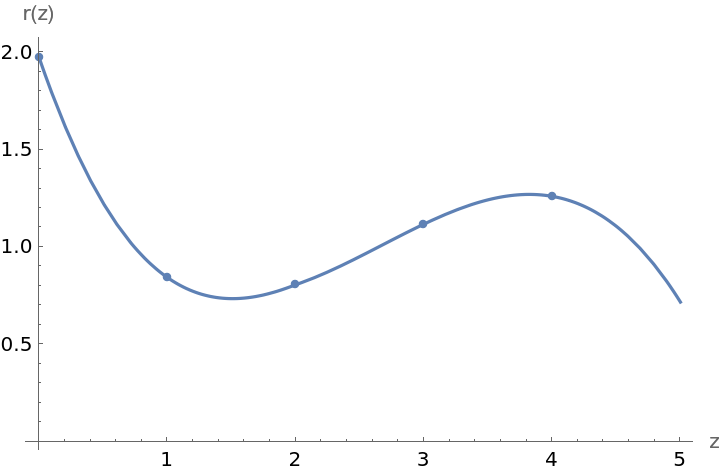
Show[ListPlot@list, Plot[ifun[x], {x, 0, n}], PlotRange -> All, AxesLabel -> {"z", "r(z)"}]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/74466e37c14f492f.png)
![normals = ResourceFunction["PlotVector3D"][
Flatten[
Table[normalVector /. r -> ifun, {\[Phi], 0, 2 \[Pi], \[Pi]/
15}, {z, 0, 4, 0.25}], 1],
Flatten[
Table[mapping /. r -> ifun, {\[Phi], 0, 2 \[Pi], \[Pi]/15}, {z, 0,
4, 0.25}], 1],
"ArrowSize" -> Small, "LocatedVector" -> False];](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/3f563ca97d409f1f.png)

![ResourceFunction["CoordinateMappingData"][mapping, "MappingJacobian", coords] == D[mapping, {coords}] == Grad[mapping, coords] == CoordinateTransformData["Cylindrical" -> "Cartesian", "MappingJacobian", coords] == ResourceFunction["JacobianMatrix"][mapping, coords]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/13a8e1715d127277.png)
![TrueQ[(ResourceFunction["CoordinateMappingData"][#[[1]], "MappingJacobian", #[[2]]] == Transpose@
ResourceFunction["CoordinateMappingData"][#[[1]], "CovariantBaseVectors", #[[2]], "UnitVectors" -> False]) &[{{r Sin[u] Cos[v], r Sin[u] Sin[v],
r Cos[u]}, {r, u, v}}] // Simplify]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/5446b9fffdf2a3a8.png)
![TrueQ[(ResourceFunction["CoordinateMappingData"][#[[1]], "MappingJacobian", #[[2]]] == Transpose@
ResourceFunction["CoordinateMappingData"][#[[1]], "CovariantBaseVectors", #[[2]], "UnitVectors" -> True]) &[{{r Sin[u] Cos[v], r Sin[u] Sin[v], r Cos[u]}, {r, u, v}}] // Simplify]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/7b968e9dab043333.png)
![TrueQ[(ResourceFunction["CoordinateMappingData"][#[[1]], "InverseMappingJacobian", #[[2]]] == ResourceFunction["CoordinateMappingData"][#[[1]], "ContravariantBaseVectors", #[[2]], "UnitVectors" -> False]) &[{{r Sin[u] Cos[v], r Sin[u] Sin[v], r Cos[u]}, {r, u, v}}] // Simplify]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/59acf0390f151a5c.png)
![TrueQ[(ResourceFunction["CoordinateMappingData"][#[[1]], "InverseMappingJacobian", #[[2]]] == ResourceFunction["CoordinateMappingData"][#[[1]], "ContravariantBaseVectors", #[[2]], "UnitVectors" -> True]) &[{{r Sin[u] Cos[v], r Sin[u] Sin[v], r Cos[u]}, {r, u, v}}] // Simplify]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/5d3c7a3e449359bf.png)
![ResourceFunction[
"CoordinateMappingData"][{(R + r Cos[#[[2]]]) Cos[#[[1]]], (R + r Cos[#[[2]]]) Sin[#[[1]]], r Sin[#[[2]]]} &, "MappingJacobian"][{u, v}] // Simplify // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/5e6832d3cffeb889.png)

![ResourceFunction[
"CoordinateMappingData"][{(R + r Cos[#[[2]]]) Cos[#[[1]]], (R + r Cos[#[[2]]]) Sin[#[[1]]], r Sin[#[[2]]]} &, "MappingJacobianDeterminant"][{u, v}]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/7d35af256b709af4.png)
![ResourceFunction[
"CoordinateMappingData"][{(R + r Cos[#[[2]]]) Cos[#[[1]]], (R + r Cos[#[[2]]]) Sin[#[[1]]], r Sin[#[[2]]]} &, "InverseMappingJacobian"][{u, v}]](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/745a5936929b5c95.png)
![ResourceFunction[
"CoordinateMappingData"][{(R + r Cos[#[[2]]]) Cos[#[[1]]], (R + r Cos[#[[2]]]) Sin[#[[1]]], r Sin[#[[2]]]} &, "ContravariantBaseVectors"][{u, v}] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/812/81241af7-4081-4251-af9d-2dbfe85051d8/715751337ec7e023.png)