Basic Examples (4)
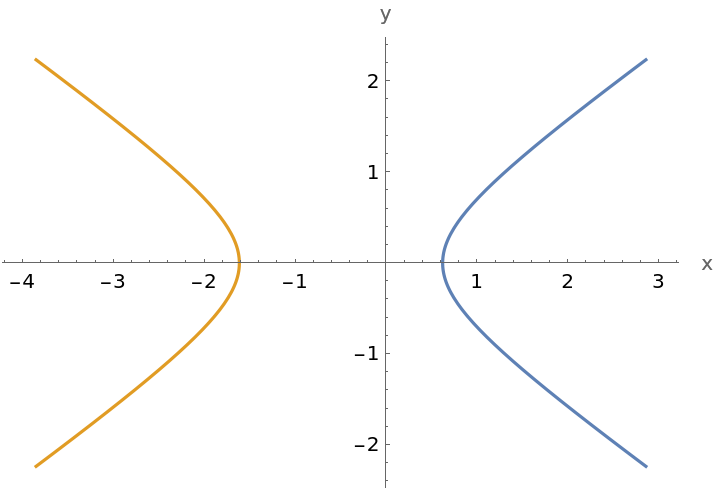
Plot a hyperbola:
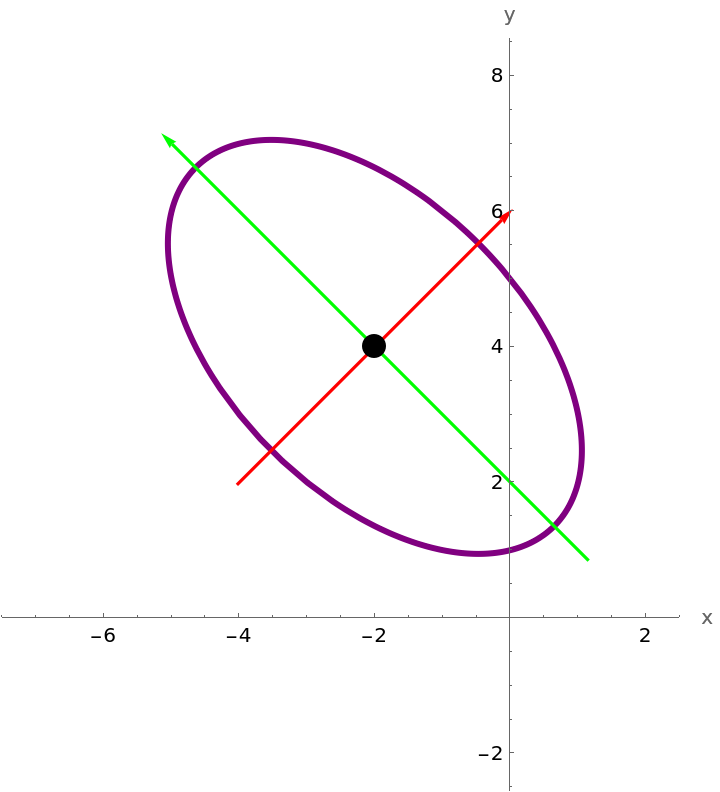
Plot a rotated and translated hyperbola and show the axes:
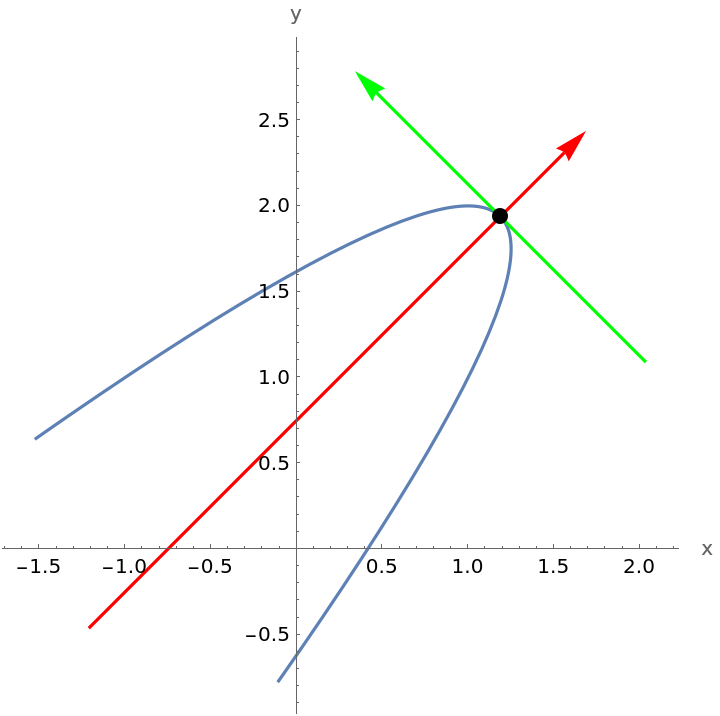
Plot a rotated and translated parabola and show the axes:
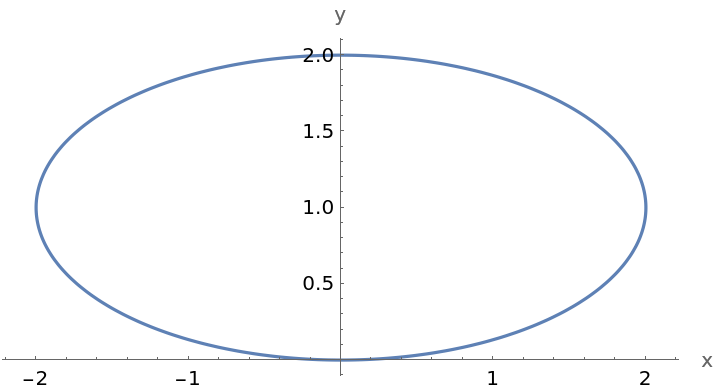
Plot an ellipse:
Scope (10)
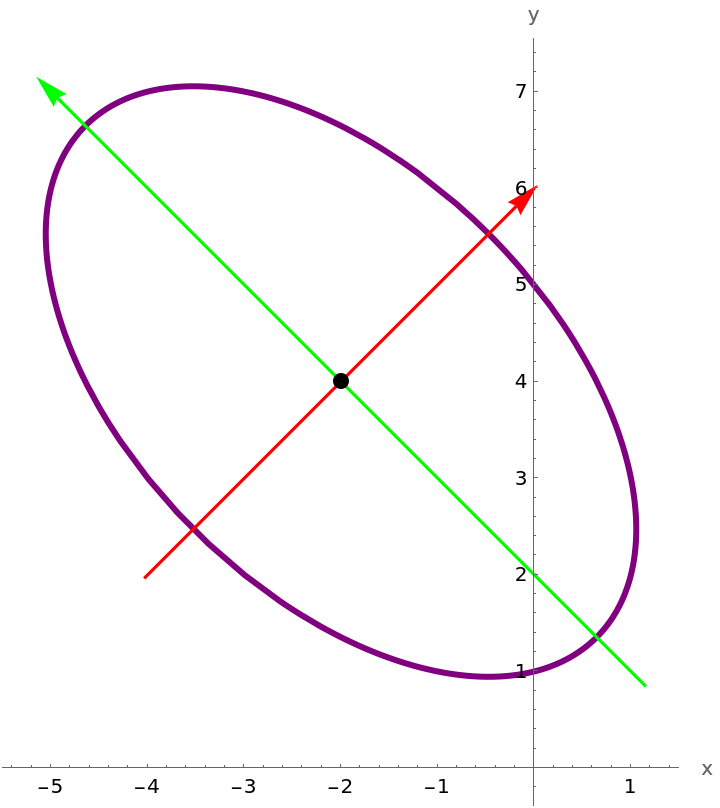
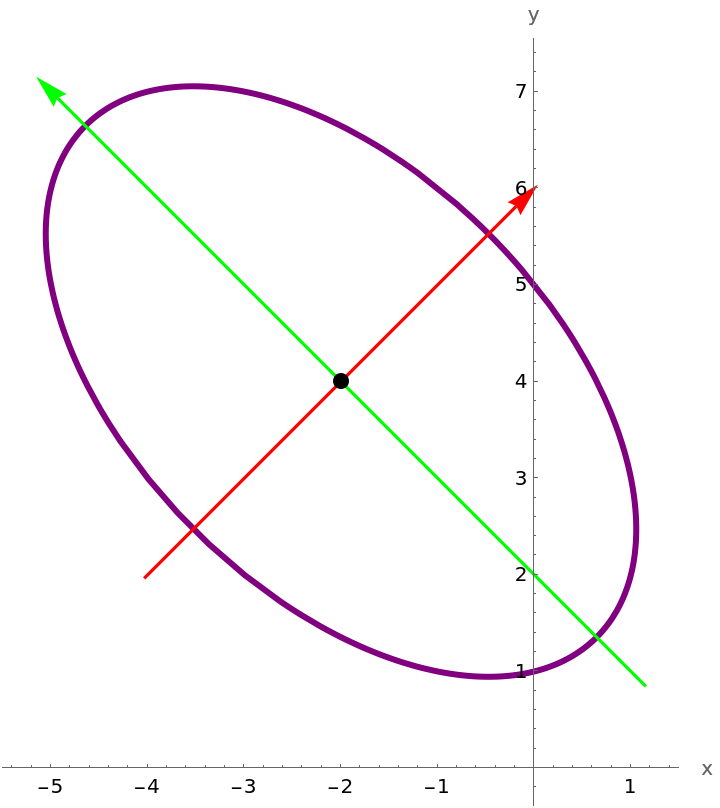
Plot a rotated and translated ellipse, with a style set for the ellipse, and show the axes:
Use "ReturnData" to examine and possibly modify the data used to produce the plot and possibly modify the data:
Make several changes to the data (shrink the arrowheads, enlarge the center point, and enlarge the plot range) and plot the result:
Compare with the original plot:
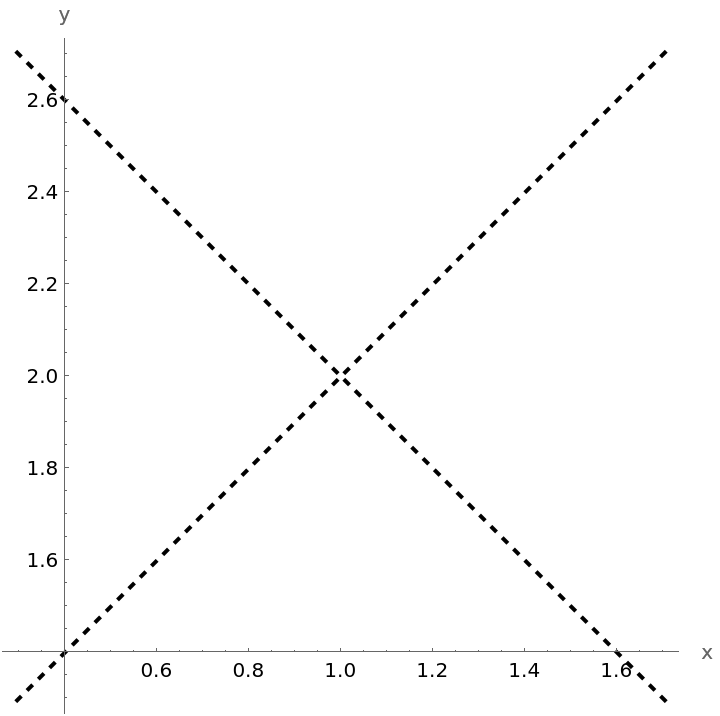
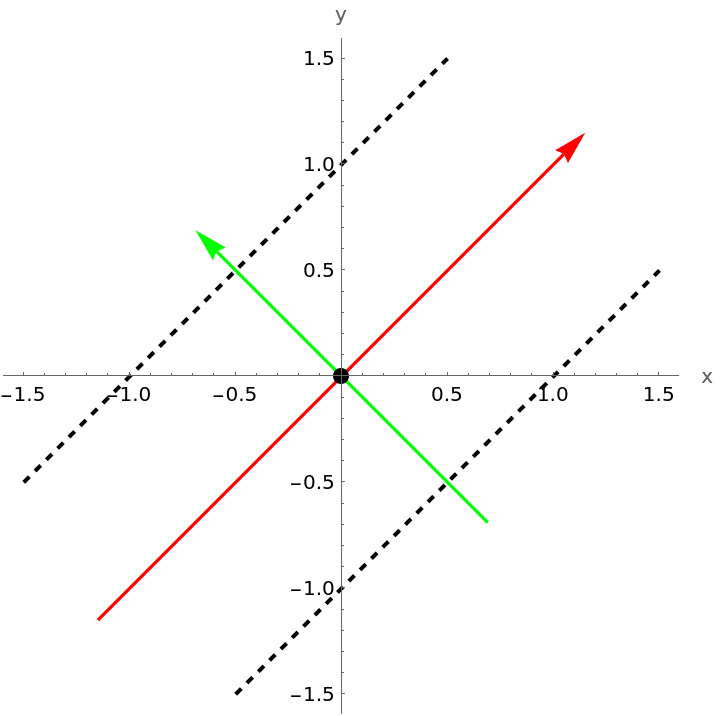
Plot a pair of intersecting lines:
These lines intersect because the polynomial can be expressed as a difference of squares. Confirm with the resource function CompleteTheSquare:
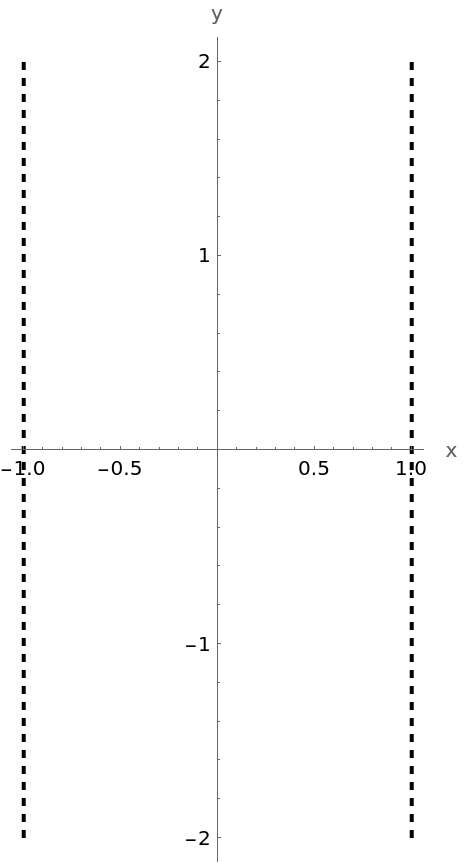
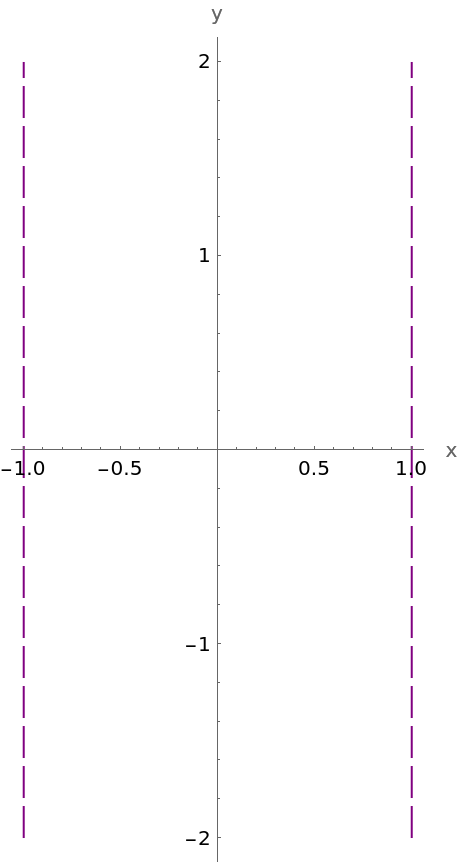
Plot a pair of parallel lines:
Change the style of the two lines using the option "PrimitivesStyle":
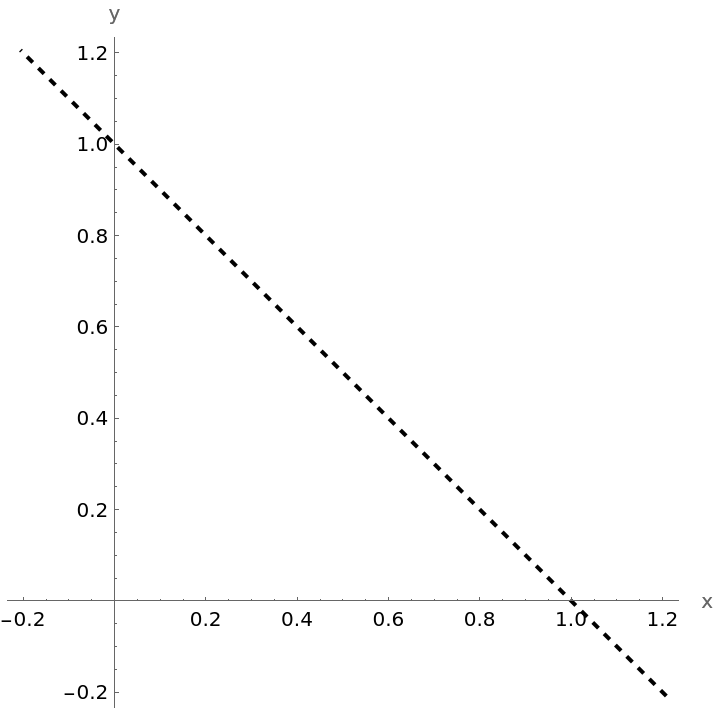
Plot an oblique line:
Plot a pair of parallel oblique lines and show the axes:
Plot a line parallel to a coordinate axis:
This equation determines the whole plane:
This equation determines the empty set:
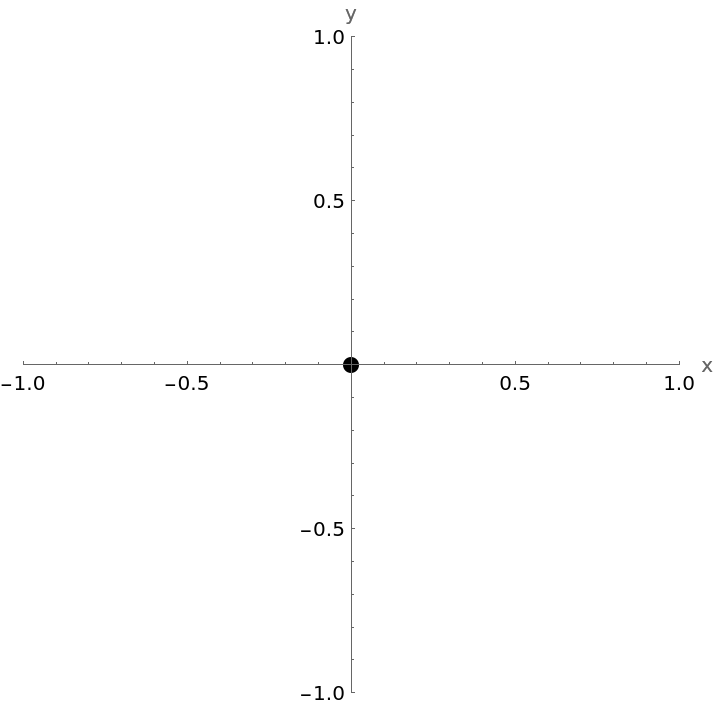
This equation determines the origin:
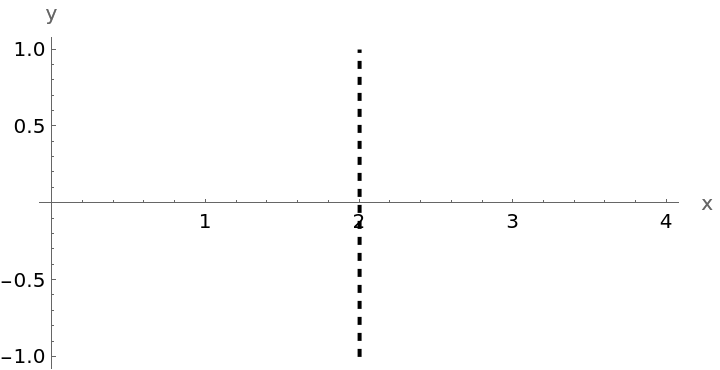
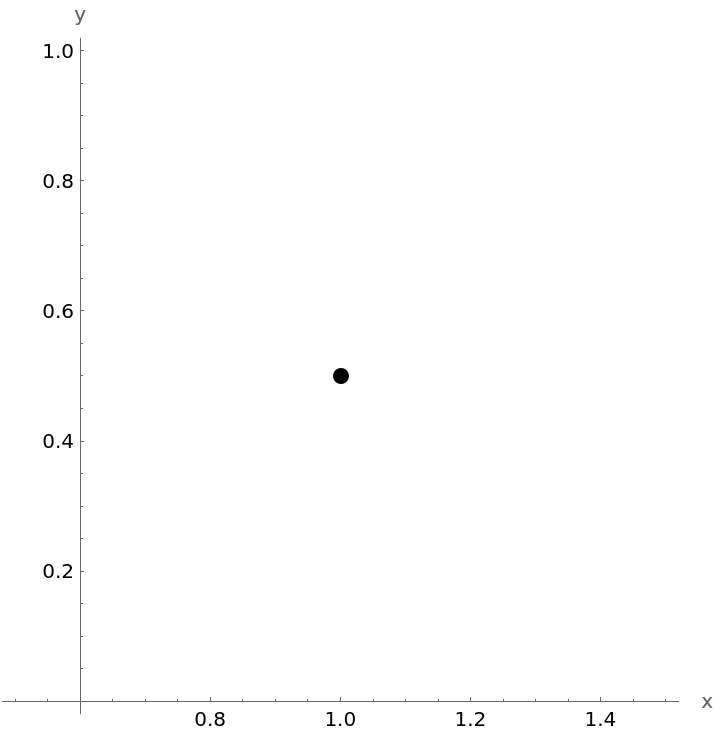
This equation determines point {1,1/2}:
Possible Issues (4)
ConicSectionPlot will returned $Failed if the degree of the quadratic is more than 2:
ConicSectionPlot will returned $Failed if the expression is not a polynomial:
ConicSectionPlot will returned $Failed if if there is not the correct number of input variables:
ConicSectionPlot will returned $Failed if the input expression is not a polynomial in the specified variables:
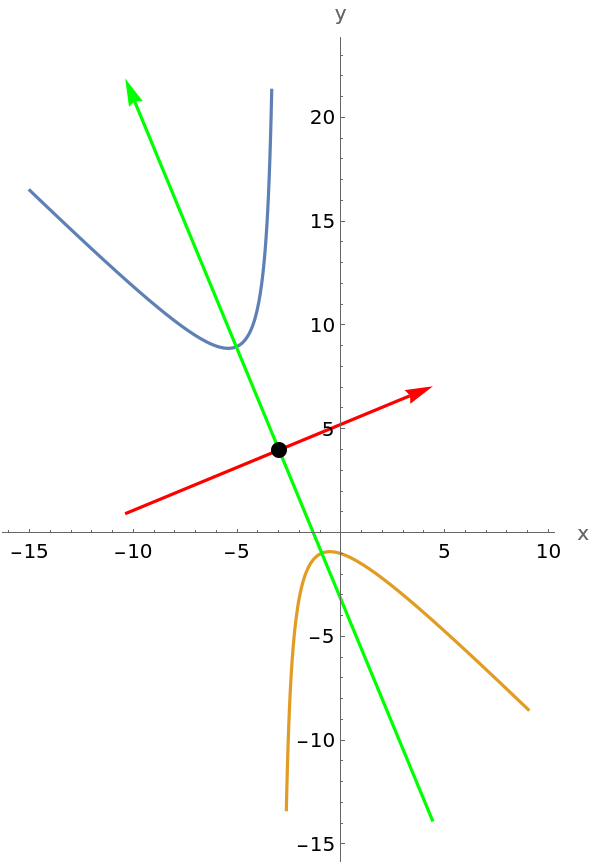

![Inactive[Show][{Inactive[
ParametricPlot][{-2.` + 1.5275252316519468` Cos[t] - 2.6457513110645903` Sin[t], 4.` + 1.5275252316519468` Cos[t] + 2.6457513110645903` Sin[t]}, {t, 0, 2 \[Pi]}, PlotStyle -> {{AbsoluteThickness[3], RGBColor[0.5, 0, 0.5]}}, AxesLabel -> {" x ", " y "}], Inactive[
Graphics][{{{AbsoluteThickness[1.6`], AbsolutePointSize[8], Arrowheads[0.025], RGBColor[1, 0, 0], Arrow[{{-4.036700308869262`, 1.963299691130738`}, {0.0367003088692619`, 6.036700308869262`}}]}, {AbsoluteThickness[1.6`], AbsolutePointSize[8], Arrowheads[0.025], RGBColor[0, 1, 0], Arrow[{{1.1549263882819059`, 0.8450736117180941`}, {-5.154926388281906`, 7.154926388281906`}}]}}, {Thickness[0.0125`], PointSize[0.04`], GrayLevel[0], AbsoluteThickness[2], Dashing[{Small, Small}], AbsolutePointSize[12], Point[{-2.`, 4.`}]}}]}, PlotRange -> {{-7, 2}, {-2, 8}}, AspectRatio -> Automatic] // Activate](https://www.wolframcloud.com/obj/resourcesystem/images/9ef/9efbcf4d-98b4-4eff-b081-ac167fb93c2c/422be28dd76d6bb0.png)