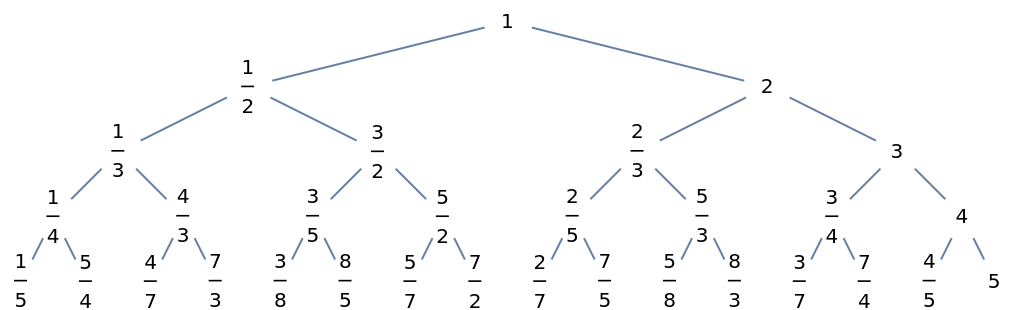
Basic Examples (2)
Find the position of 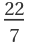 in the Calkin–Wilf sequence:
in the Calkin–Wilf sequence:
Find the position of 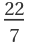 in the Calkin–Wilf sequence with explicit numerator and denominator:
in the Calkin–Wilf sequence with explicit numerator and denominator:
Find the fraction at position 519 in the Calkin–Wilf sequence:
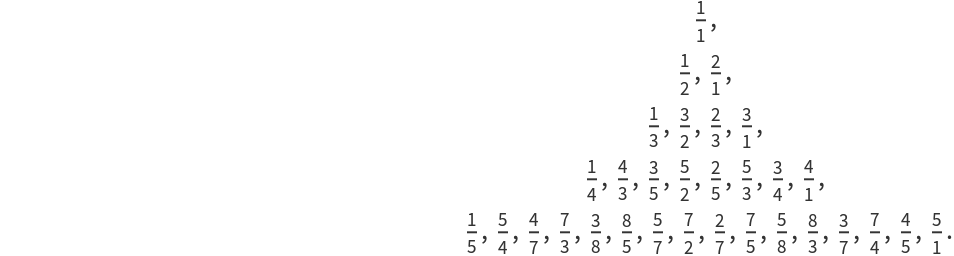
Generate terms of the Farey sequence:
Show their positions in the Calkin–Wilf sequence:
Use the positions to generate fractions:
Scope (4)
Show the first 42 terms:
Get back the positions using explicit numerators and denominators:
Get back the positions by forcing a denominator of 1 everywhere:
A two term form is needed for positions of integers since fractions  ,
, ,
, ,
, are returned as 1, 2, 3, 4:
are returned as 1, 2, 3, 4:
Properties and Relations (7)
Negative values return negative fractions:
Negative fractions correspond to negative positions:
Terms 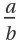 and
and 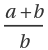 are at positions k and 2k+1:
are at positions k and 2k+1:
Level 5 of the Calkin–Wilf tree:
Find the Total of the terms of the ContinuedFraction for level 5 of the Calkin–Wilf tree:
For terms 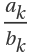 on the same level in the Calkin–Wilf tree,
on the same level in the Calkin–Wilf tree, 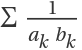 =1:
=1:
The maximal numerator for level n of the Calkin–Wilf tree is Fibonacci[n+1]:
An unreduced fraction gives the same value as the reduced fraction:
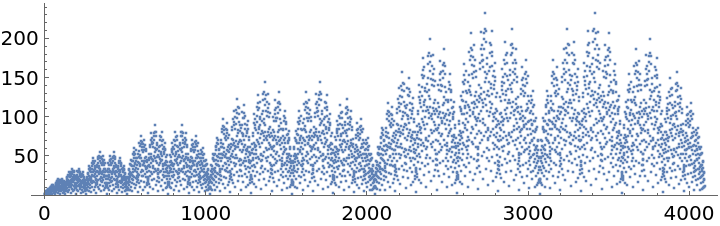
Create a plot of the first 256 values:
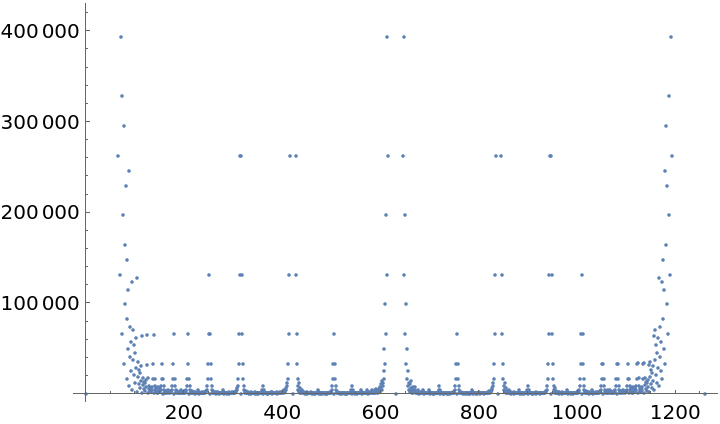
Create a plot of indices for the Farey sequence fractions:
Possible Issues (3)
Fractions at positions 2a-1 are returned as a instead of 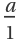 :
:
CalkinWilf returns a Failure if its input is anything other than an rational:
Fractions leading to an index with more than a million digits will be flagged as out of range:
Fractions with a million digit index will be evaluated as expected:
Neat Examples (2)
Show the Calkin–Wilf binary tree with nodes of type 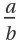 and sub-nodes
and sub-nodes 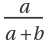 and
and 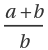 :
:
List the denominators of the Calkin–Wilf sequence:
Prepend a 1 to get the numerators of the Calkin–Wilf sequence:
This is also known as the Fusc sequence:
Plot the Fusc sequence:
![]() in the Calkin–Wilf sequence:
in the Calkin–Wilf sequence:![]() in the Calkin–Wilf sequence with explicit numerator and denominator:
in the Calkin–Wilf sequence with explicit numerator and denominator: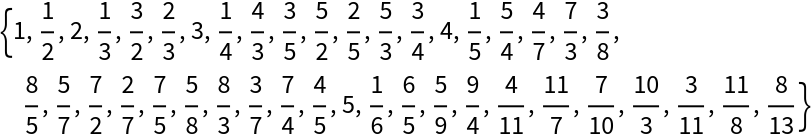
![]() ,
,![]() ,
,![]() ,
,![]() are returned as 1, 2, 3, 4:
are returned as 1, 2, 3, 4: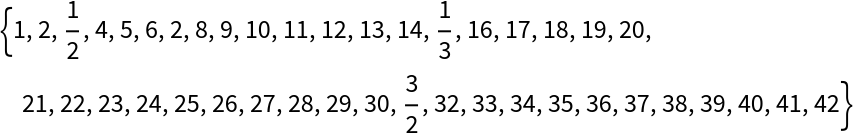
![]() and
and ![]() are at positions k and 2k+1:
are at positions k and 2k+1: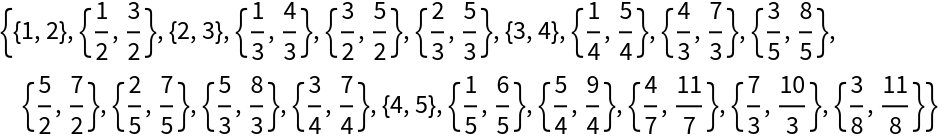
![]() on the same level in the Calkin–Wilf tree,
on the same level in the Calkin–Wilf tree, ![]() =1:
=1: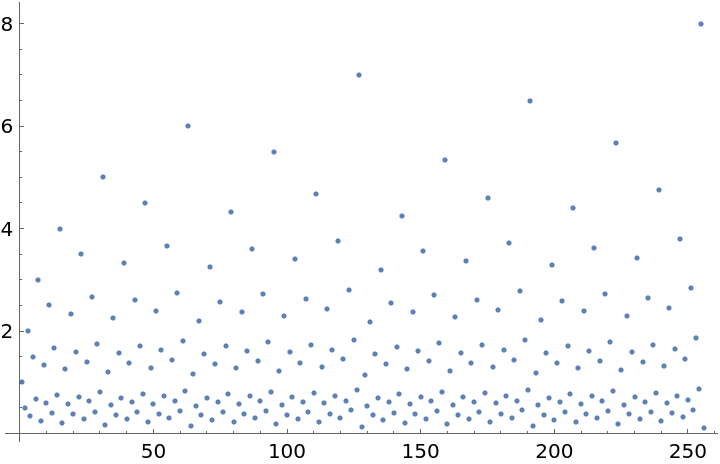
![]() :
:
![]() and sub-nodes
and sub-nodes ![]() and
and ![]() :
:![Graph[EdgeList[CompleteKaryTree[5, 2]] /. Thread[Range[31] -> ResourceFunction["CalkinWilf"][Range[31]]], VertexLabels -> Placed[Automatic, Center], VertexSize -> .75, VertexShapeFunction -> Nothing]](https://www.wolframcloud.com/obj/resourcesystem/images/b85/b858f4c0-3708-4d25-8ca9-f20347f3a3a9/48a4131b22b21e49.png)