Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BrocardInellipse

Source Notebook

Generate the Brocard inellipse of a 2D triangle

Contributed by: Jan Mangaldan

ResourceFunction["BrocardInellipse"][{p1,p2,p3}]

returns an Ellipsoid representing the Brocard inellipse of the triangle defined by vertices p1,p2, and p3.

ResourceFunction["BrocardInellipse"][{p1,p2,p3},property]

gives the value of the specified property.

Details

The Brocard inellipse of a triangle is the unique ellipse inscribed in a triangle whose foci are the Brocard points.
The following properties are supported:
"Ellipsoid"Ellipsoid representing the inellipse
"Parametric"parametric equation for the inellipse as a pure function
"Implicit"implicit Cartesian equation for the inellipse as a pure function
ResourceFunction["BrocardInellipse"][poly] where poly is a Triangle or Polygon is equivalent to ResourceFunction["BrocardInellipse"][PolygonCoordinates[poly]].

Examples

Basic Examples (1) 

Show a triangle together with its Brocard inellipse:

In[1]:=
tri = {{0, 0}, {1.2, 4}, {5, 0}}; Graphics[{FaceForm[], {EdgeForm[Red], Triangle[tri]}, {EdgeForm[Blue], ResourceFunction["BrocardInellipse"][tri]}}]
Out[1]=

Scope (5) 

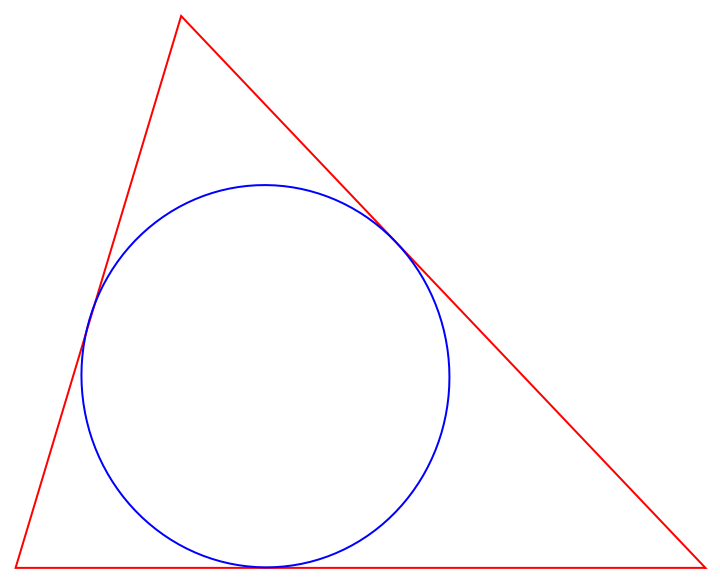A triangle:

In[2]:=
Graphics[tri = Triangle[{{0, 0}, {0.4, 3.1}, {5, 0}}]]
Out[2]=

Generate the parametric equation of the triangle's Brocard inellipse:

In[3]:=
ell1[t_] = ResourceFunction["BrocardInellipse"][tri, "Parametric"][t]
Out[3]=

Plot the parametric equation along with the triangle:

In[4]:=
Show[Graphics[{FaceForm[], EdgeForm[ColorData[97, 4]], tri}], ParametricPlot[ell1[t], {t, 0, 2 \[Pi]}]]
Out[4]=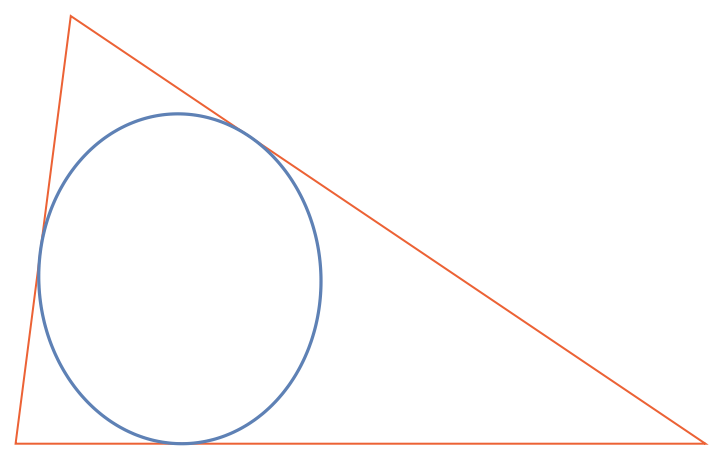

Generate the implicit equation of the triangle's Brocard inellipse:

In[5]:=
ell2[x_, y_] = ResourceFunction["BrocardInellipse"][tri, "Implicit"][x, y]
Out[5]=

Plot the implicit equation along with the triangle:

In[6]:=
ContourPlot[ell2[x, y] == 0, {x, -1, 6}, {y, -1, 4}, AspectRatio -> Automatic, Epilog -> {FaceForm[], EdgeForm[ColorData[97, 4]], tri}]
Out[6]=

Properties and Relations (2) 

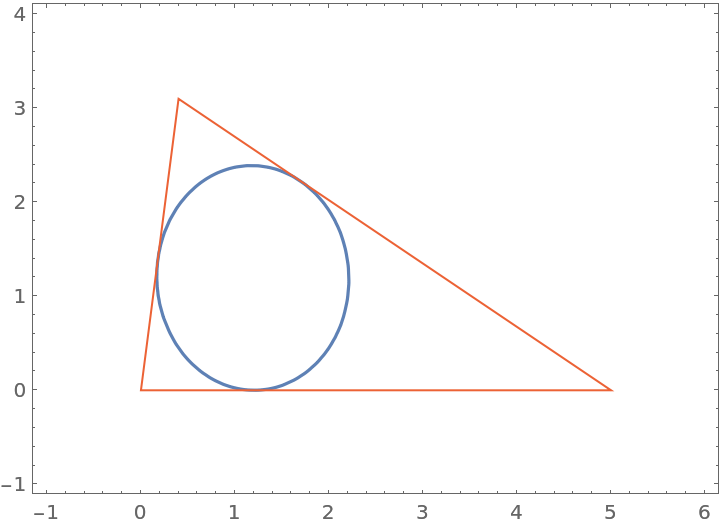Use the resource function EllipseProperties to generate properties of the inellipse:

In[7]:=
tri = {{0, 0}, {1.1, 4}, {5, 0}}; prop = ResourceFunction["EllipseProperties"][ ResourceFunction["BrocardInellipse"][tri, "Implicit"][x, y] == 0, {x, y}]
Out[7]=

The foci of the inellipse are the Brocard points of the triangle:

In[8]:=
bp = Lookup[prop, "Foci"]
Out[8]=

Show that the angles formed by the Brocard points and the triangle's vertices are all equal to the Brocard angle:

In[9]:=
PlanarAngle[Prepend[#, bp[[1]]]] & /@ Partition[tri, 2, 1, 1]
Out[9]=
In[10]:=
PlanarAngle[Prepend[#, bp[[2]]]] & /@ Reverse[Partition[tri, 2, 1, 1], 2]
Out[10]=
In[11]:=
ArcTan[Total[SquaredEuclideanDistance @@@ Partition[tri, 2, 1, 1]], 4 Area[Triangle[tri]]]
Out[11]=

The area of the Brocard inellipse can be expressed in terms of the area of the original triangle and the lengths of its sides:

In[12]:=
tri = {{0, 0}, {1.5, 4}, {5, 0}}; Area[ResourceFunction["BrocardInellipse"][tri]]
Out[12]=
In[13]:=
sl = SquaredEuclideanDistance @@@ Partition[tri, 2, 1, 1]; (\[Pi] SymmetricPolynomial[3, sl])/SymmetricPolynomial[2, sl]^(3/2) Area[Triangle[tri]]
Out[13]=

Version History

  • 1.0.1 – 24 August 2021

Related Resources

License Information