Function Repository Resource:

BiasedRescale

Source Notebook

Bias a value in the unit interval either lower or higher

Contributed by: Jan Mangaldan

ResourceFunction["BiasedRescale"][a,x]

biases x toward lower values if a<1/2 and toward higher values if a>1/2 as x runs from 0 to 1.

ResourceFunction["BiasedRescale"][a,x,{min,max}]

biases x as x runs from min to max.

ResourceFunction["BiasedRescale"][a,x,{min,max},{y_min,y_max}]

biases x as x runs from min to max, with the result rescaled to run from y_min to y_max.

Details and Options

a can be any real number between 0 and 1.

The result of ResourceFunction["BiasedRescale"][a,x,{min,max}] is always between 0 and 1.

ResourceFunction["BiasedRescale"] can take the Method option for the bias function to use.

Possible settings for the Method option are "Schlick" (default) and "Perlin".

With the default option setting Method→"Schlick", ResourceFunction["BiasedRescale"] uses Schlick's bias function x/((1/a-2)(1-x)+1).

With Method→"Perlin", ResourceFunction["BiasedRescale"] uses Perlin's bias function x^-log₂(a).

ResourceFunction["BiasedRescale"] is commonly used in computer graphics.

Examples

Basic Examples (3)

Evaluate numerically:

In[1]:=

Out[1]=

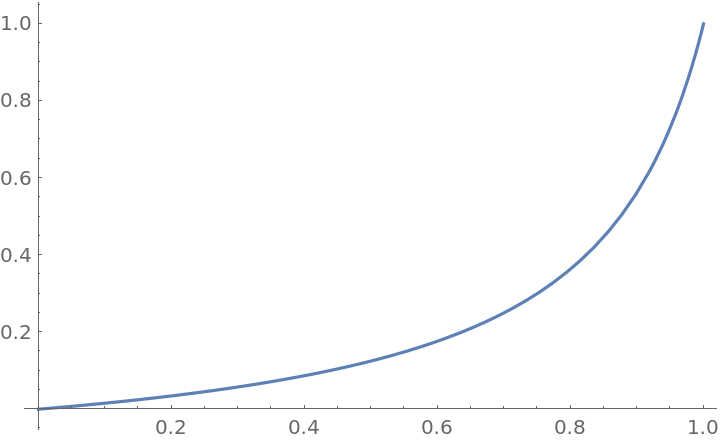
Plot over a subset of the reals:

In[2]:=

Out[2]=

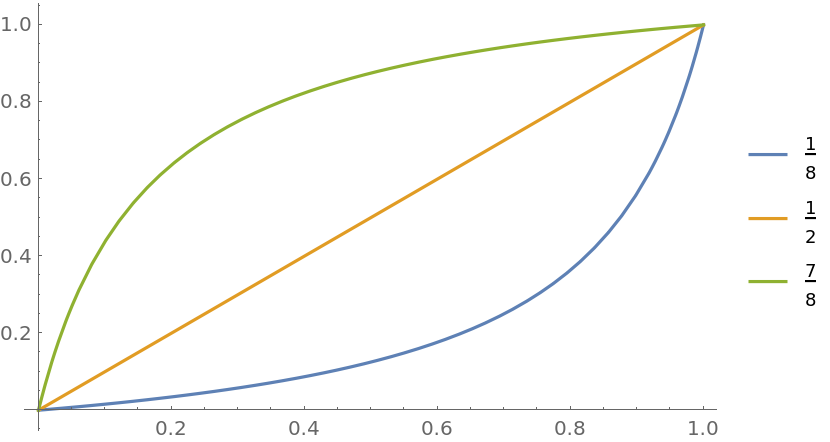
Plot different bias functions:

In[3]:=

Out[3]=

Scope (4)

Evaluate for symbolic x:

In[4]:=

Out[4]=

BiasedRescale threads over lists in its first and second arguments:

In[5]:=

Out[5]=

In[6]:=

Out[6]=

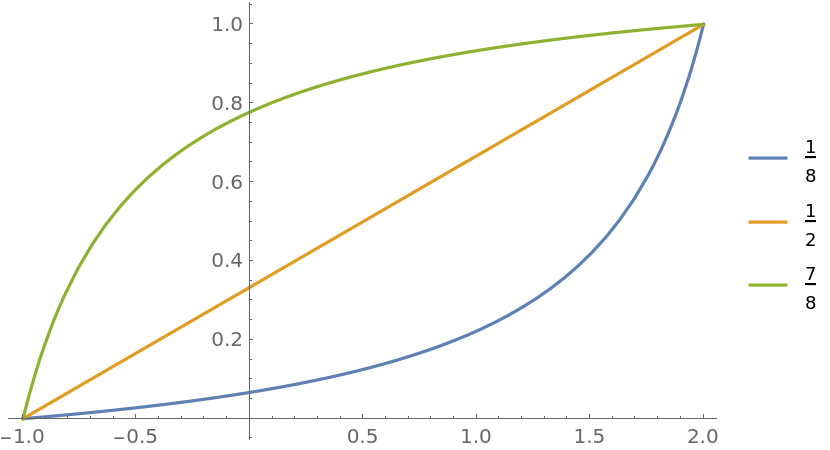
Plot different bias functions with a rescaled domain:

In[7]:=

Out[7]=

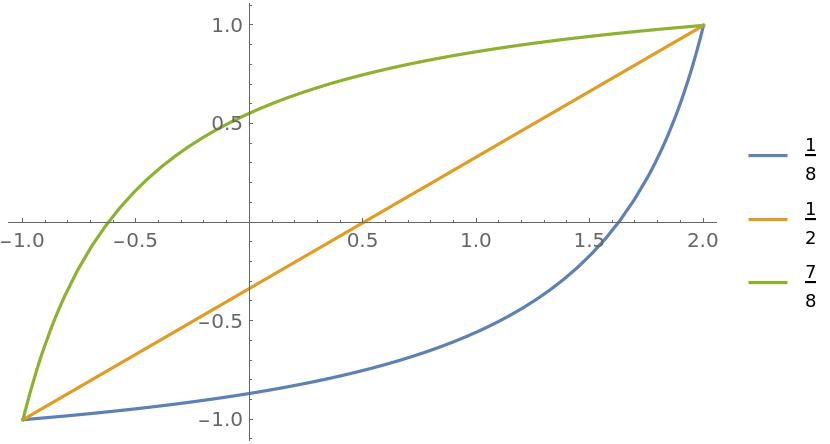
Plot different bias functions with a rescaled domain and range:

In[8]:=

Out[8]=

Options (1)

Method (1)

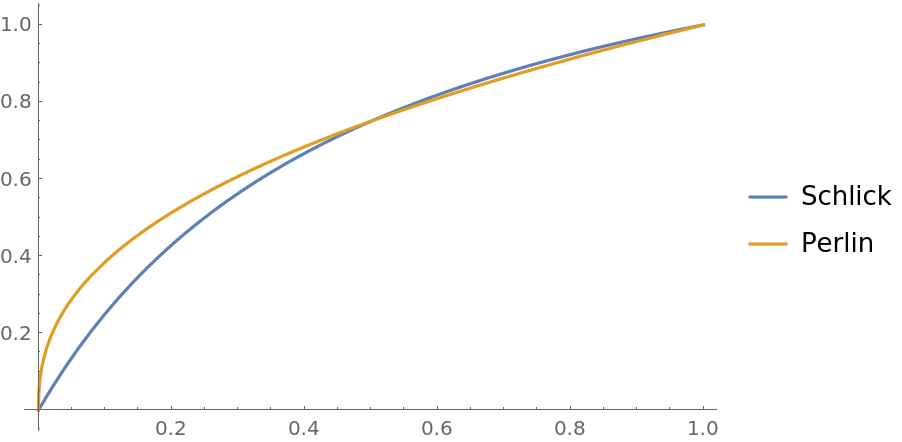
Compare the Schlick and Perlin bias functions:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

Applications (2)

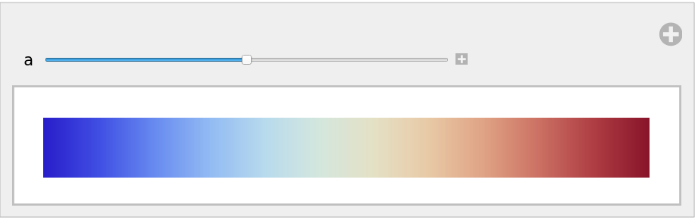
Adjust the middle color of a built-in color gradient:

In[11]:=

Out[11]=

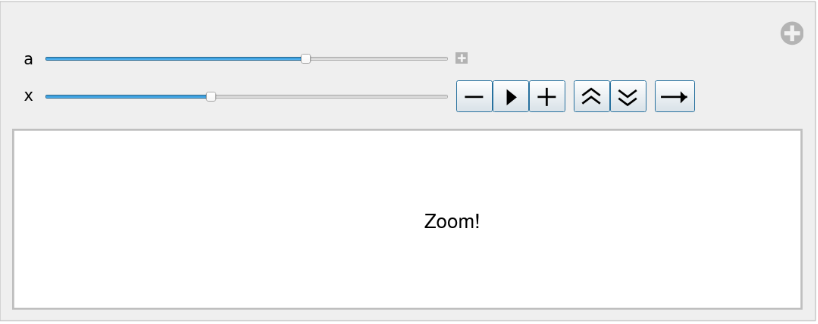
Demonstrate the effect of BiasedRescale on easing in/easing out:

In[12]:=

Manipulate[
Graphics[Text[
"Zoom!", {ResourceFunction["BiasedRescale"][a, x, {-1, 2}], 0}], PlotRange -> {{-0.1, 1.1}, {-0.1, 0.1}}], {{a, 1/2}, 0, 1}, {x, -1, 2, ControlType -> Animator, AnimationRunning -> False}]

Out[12]=

Properties and Relations (1)

BiasedRescale[1/2,x,{min,max}] is equivalent to Rescale[x,{min,max}]:

In[13]:=

Out[13]=

Possible Issues (2)

BiasedRescale is left unevaluated if the first argument is non-numeric:

In[14]:=

Out[14]=

BiasedRescale is left unevaluated if the first argument is not a real number between 0 and 1:

In[15]:=

Out[15]=

Neat Examples (6)

Use BiasedRescale with the resource function GaussianQuadratureWeights to evaluate a Cauchy principal value integral.

The function to be integrated and the integration limits:

In[16]:=

f[x_] := E^x/x;
xmin = -1.; xmax = 3.;

Even-order Gaussian quadrature abscissas and weights:

In[17]:=

The transformation function to be applied to the abscissas and weights:

In[18]:=

$tr[x_] = ResourceFunction["BiasedRescale"][Rescale[0, {xmin, xmax}], x, {xmin, xmax}, {xmin, xmax}];$

Transform the abscissas and weights:

In[19]:=

Out[19]=

In[20]:=

Out[20]=

Compute the integral:

In[21]:=

Out[21]=

Compare with the result of NIntegrate:

In[22]:=

Out[22]=

Version History

1.0.1 – 16 February 2021
1.0.0 – 28 December 2020

Source Metadata

Citation:
- Perlin K., Hoffert E.M., Hypertexture. SIGGRAPH ‘89: Proceedings of the 16th annual conference on Computer graphics and interactive techniques, 253-262, 1989 DOI: 10.1145/74333.74359
- Schlick C., Fast alternatives to Perlin’s bias and gain functions. Graphics Gems IV, 401-403, 1994 DOI: 10.1016/B978-0-12-336156-1.50050-1

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License