Function Repository Resource:

BernoulliBTree

Source Notebook

Generate a binary tree representation of Bernoulli numbers by Woon's method

Contributed by: Shenghui Yang

ResourceFunction["BernoulliBTree"][n]

generates a binary tree representation of Bernoulli numbers with n levels by Woon's method.

ResourceFunction["BernoulliBTree"][n,prop]

uses the specified property for tree nodes.

Details

Each element {a,b,c,…,±1} in the binary tree is the list representation for

. For instance, {4,2,1} corresponds to 1/(4!·2!) = 1/48.

For each element {a,b,c,…,±1} in the binary tree, its children are {a+1,b,c,…,∓1} and {2,a,b,c,…,±1}.

The n-th Bernoulli number is n! times the sum of the corresponding factorial fractions in the (n-1)-th row, except for the root node. A more detailed step-by-step construction is available in the Neat Examples section below.

The available properties are "FactorialComponents" and "SummandForm". "FactorialComponents" is the default setting with the tree node in the form of {a,b,c,…,±1}. "SummandForm" computes the corresponding factorial fraction for each node from the list form.

Examples

Basic Examples (2)

Generate a Bernoulli tree with 3 levels with factorial components:

In[1]:=

Out[1]=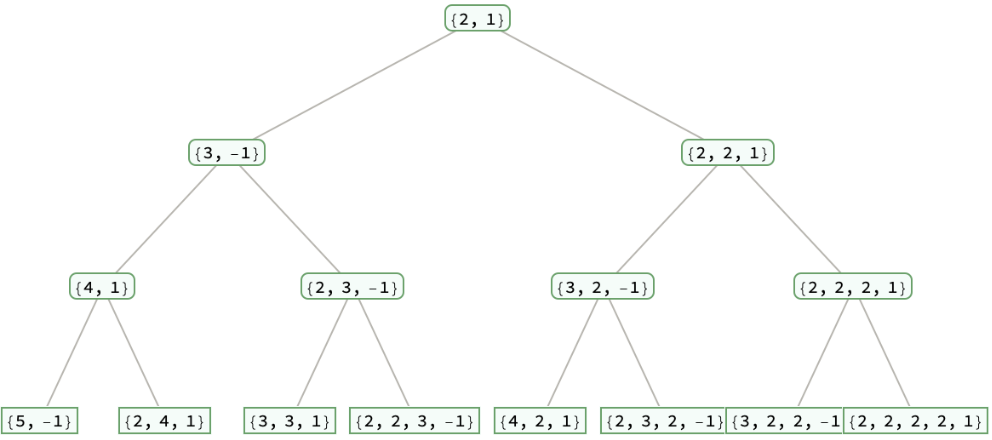

Generate a Bernoulli tree with 4 levels with numeric values from the factorial components:

In[2]:=

Out[2]=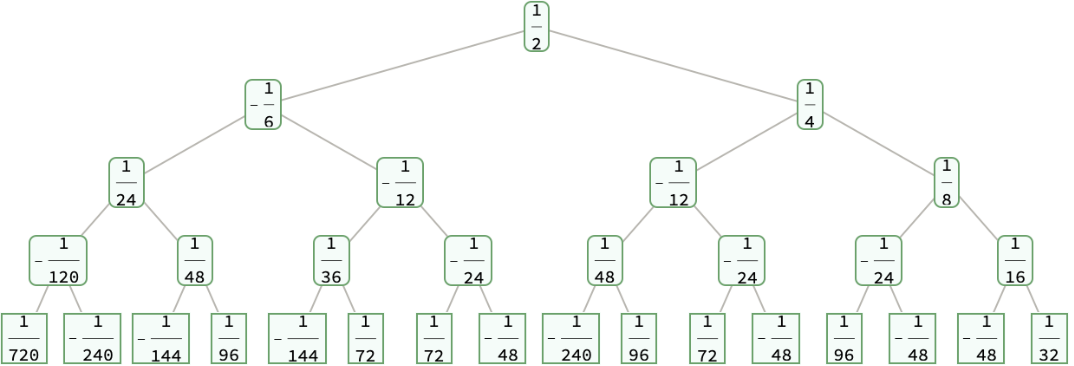

Scope (3)

It is easy to convert the binary tree to an actual Bernoulli number:

In[3]:=

Out[3]=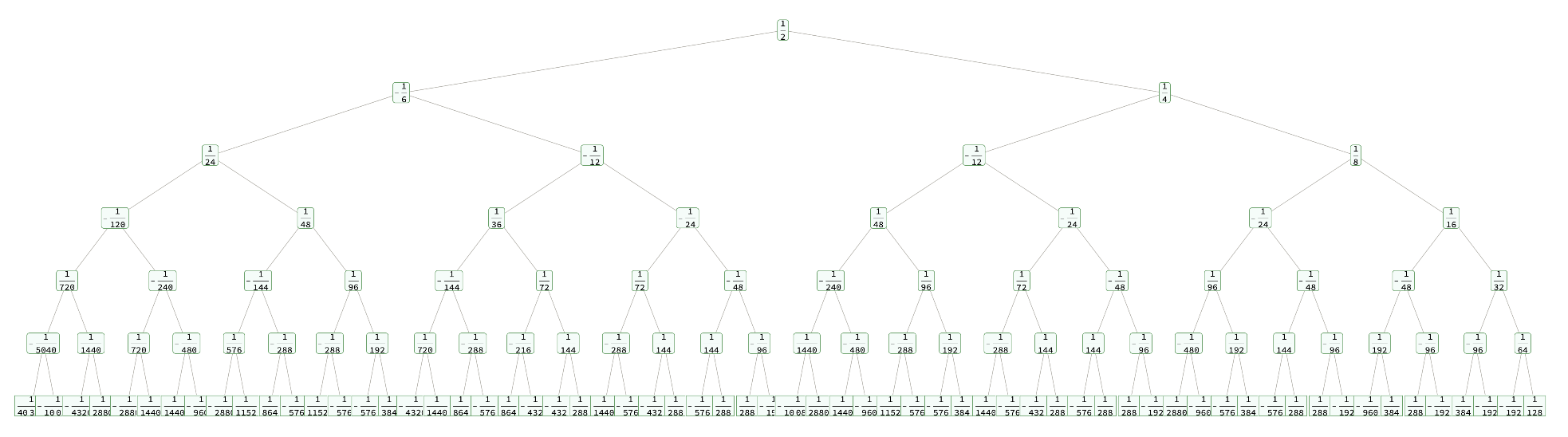

Tabulate the results from the function to that from the built-in BernoulliB function:

In[4]:=

ResourceFunction["NiceGrid"][{
{Table[Total[k!*TreeData /@ TreeLevel[bbt, {k - 1}]], {k, 2, 6}]},
{BernoulliB[Range[2, 6]]}
}, {}, {"From binary tree", "From Built-in function"}, Alignment -> Left]

Out[4]=

Only the root item in the tree is an exception:

In[5]:=

Out[5]=

Applications (2)

Define a simple check to determine if a given list is an element on the binary tree:

In[6]:=

$test[input_List] /; AllTrue[input, IntegerQ] := ((Last[input]^2 - 1) == 0 && (input[[1]] >= 2) && {2, 1} == NestWhile[ If[#[[1]] == 2, Rest[#], {#[[1]] - 1}~Join~(#[[2 ;; -2]])~ Join~({-#[[-1]]})] &, input, (# != {2, 1} && Length[#] >= 2 &), 1, Abs[Total[input]]] )$

In[7]:=

Out[7]=

In[8]:=

Out[8]=

In[9]:=

Out[9]=

It is also possible to use umbral calculus technique based on the set of functions that creates left and right child in the binary tree. Let's define the expansion method on the non-commutative multiplication first:

In[10]:=

In[11]:=

In[12]:=

In[13]:=

Define the root node and child-generation functions:

In[14]:=

In[15]:=

In[16]:=

Define the conversion formula from the lists in the tree to the factorial fraction:

In[17]:=

For instance, the 4th Bernoulli number corresponds to this expression in the binary tree:

In[18]:=

$ExpandNCM[\[FormalH] \[CircleTimes] (Sequence @@ CirlePower[(\[FormalX] + \[FormalY]), 3])]$

Out[18]=

In[19]:=

$4!*Through[(% /. {CircleTimes -> Composition, \[FormalX] -> f, \[FormalY] -> g, \[FormalH] -> fValue})[init], Plus]$

Out[19]=

Use the same method on more items:

In[20]:=

$Map[With[{rowFunc = ExpandNCM[ \[FormalH] \[CircleTimes] Sequence @@ CirlePower[(\[FormalX] + \[FormalY]), # - 1]]}, #!*Through[(rowFunc /. {CircleTimes -> Composition, \[FormalX] -> f, \[FormalY] -> g, \[FormalH] -> fValue})[init], Plus]] &, Range[2, 10] ]$

Out[20]=

The result above is the same as those from BernoulliB:

In[21]:=

Out[21]=

Possible Issues (1)

The Bernoulli binary tree grows exponentially. A hard limit of 12 is set for the input:

In[22]:=

Out[22]=

Neat Examples (2)

If MaTeX is installed, one can use TEX form to display the conversion formula:

In[23]:=

In[24]:=

Create a binary tree and store the position of each element in a HashTable:

In[25]:=

bbt = ResourceFunction["BernoulliBTree"][8];
ht = CreateDataStructure["HashTable"];
TreeScan[ht["Insert", #1 -> fDisplay[#2]] &, bbt, All -> {"Position", "Data"}];
lvlht = Sort /@ GroupBy[ht["Keys"], Length];

Show the conversion formula from a row in the tree to the corresponding Bernoulli number:

In[26]:=

ResourceFunction[
ResourceObject[<|"Name" -> "InheritedBlock", "ShortName" -> "InheritedBlock", "UUID" -> "c9ee7074-bc6b-4a85-81da-675e443331f1", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Similar to Block, except values of local symbols are not cleared when entering the block", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$e037afc679a943928d9608206e9f6b9e`InheritedBlock", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/objects/78b4d6f3-cbaf-4935-a24a-5ab248e39b76"]|>, ResourceSystemBase -> Automatic]][{Plus},
ClearAttributes[Plus, Orderless];
rowSum = Table[Inactive[Factorial][
k]*(Inactive[
Plus] @@ ((ht["Lookup", #] & /@ lvlht[k - 1]))), {k, 2, 7}]
];

We can show a truncated part of the formula:

In[27]:=

ImageTake[Rasterize[TableForm[
Table[{MaTeX[TeXForm[rowSum[[n - 1]]], Magnification -> 1.1]}, {n, 2, 7}]
], ImageResolution -> 250], {2, 850}, {1, 3250}]

Out[27]=

To find the actual Bernoulli number from the formula above, simply apply Activate function to rowSum:

In[28]:=

Out[28]=

It is also possible to use MaTeX function on the nodes of a binary tree:

In[29]:=

Use TreeElementShapeFunction to apply MaTeX function on the nodes of the Bernoulli binary tree with 4 levels:

In[30]:=

Tree[ResourceFunction["BernoulliBTree"][4],
TreeElementShapeFunction -> {
All -> (
Inset[
Graphics[{{Cyan, Disk[]}, Inset[MaTeX[TeXForm[fDisplay[#2]], Magnification -> 1.2], {0, 0}]}], #, Center, 4.8*#3] &)},
TreeElementSize -> All -> Large, TreeElementLabel -> All -> None,
AspectRatio -> 1/3, ImageSize -> 860, ImagePadding -> 12
] // Framed

Out[30]=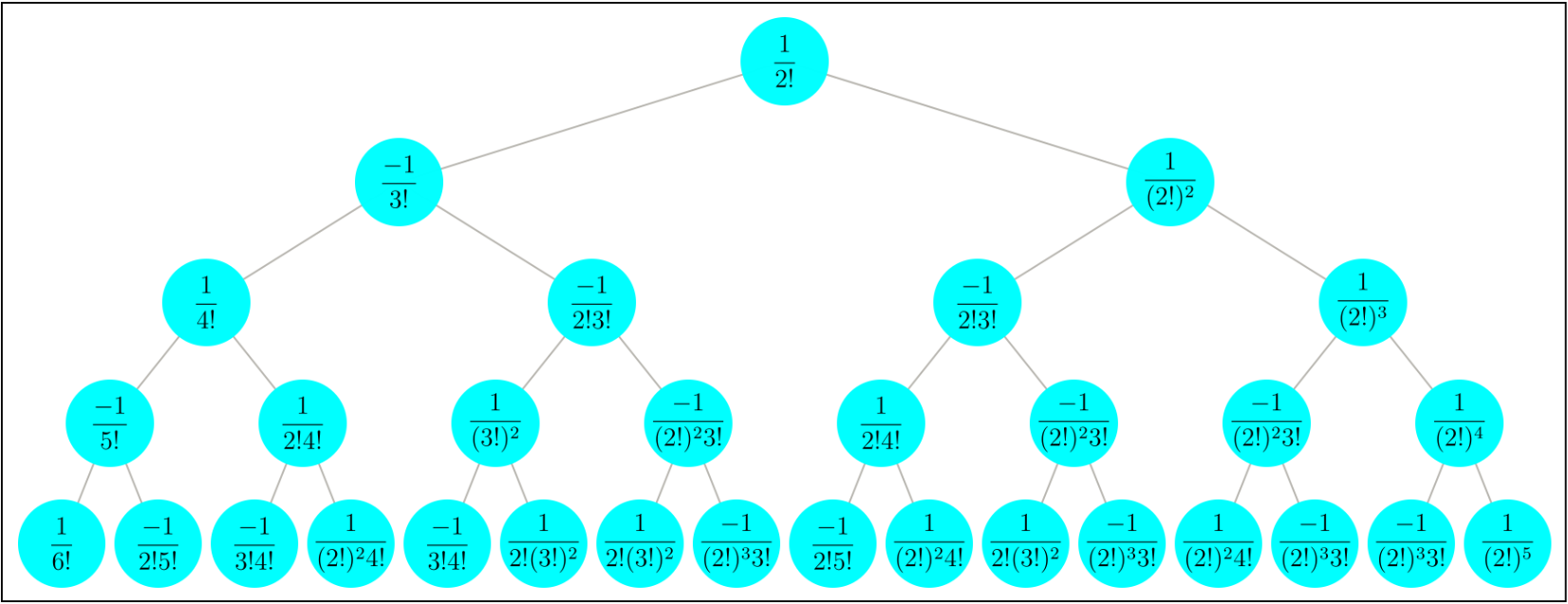

Or one can use the same code on a subtree with 4 levels. Some adjustment for Magnification in MaTeX function is recommended because the length of the denominators grow with different speed according the node position in the tree:

In[31]:=

In[32]:=

Tree[subt,
TreeElementShapeFunction -> {
All -> (
Inset[
Graphics[{{Cyan, Disk[]}, Inset[MaTeX[TeXForm[fDisplay[#2]], Magnification -> 1.2], {0, 0}]}], #, Center, 4.9*#3] &)},
TreeElementSize -> All -> Large,
TreeElementLabel -> All -> None,
AspectRatio -> 1/3, ImageSize -> 1260, ImagePadding -> 15
] // Framed

Out[32]=

Publisher

Shenghui Yang

Requirements

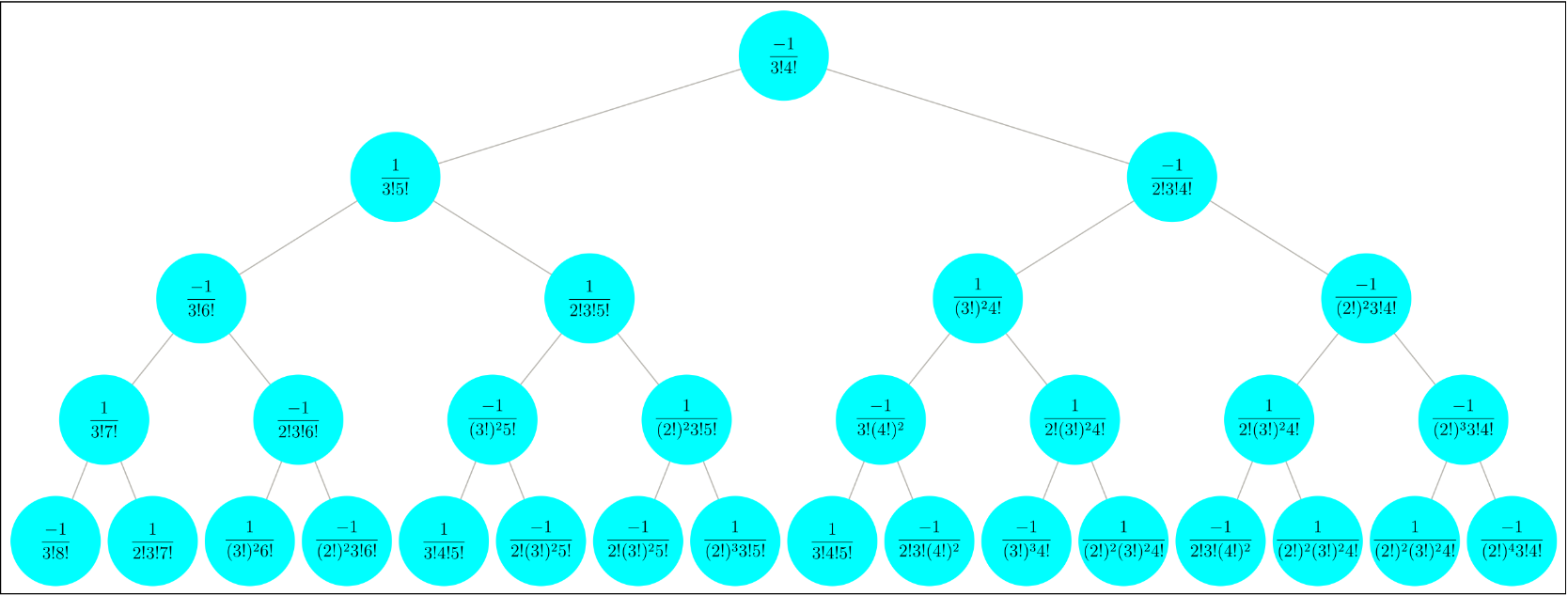Wolfram Language 14.0 (January 2024) or above

Version History

1.0.0 – 14 August 2024

Source Metadata

Citation:
- Woon, S. C. "A Tree for Generating Bernoulli Numbers." Mathematics Magazine 70, no. 1 (1997): 51–56. DOI: 10.2307/2691054.
- C. Vignat, T. Wakhare, "Woon's tree and sums over compositions", arXiv:1706.00165[math.CO]
- Woon, S. C., “A New Representation of the Riemann Zeta Function”, arXiv:math/9812143v1[math.NT]
- Weisstein, Eric W. “Bernoulli Number.” From MathWorld--A Wolfram Web Resource.
- Weisstein, Eric W. Umbral Calculus. From MathWorld--A Wolfram Web Resource.

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

BernoulliBTree

Details