Basic Examples (1) 

Create a two level Barning-Hall (B-H) tree with Fibonacci matrices as nodes:

In[1]:=

Out[1]=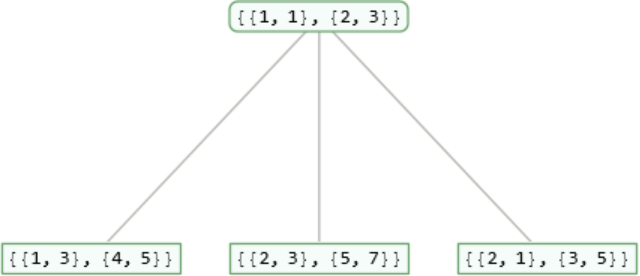

Scope (1) 

Use "LabeledWithPythagoreanTriples" property to display the B-H tree together with its associated primitive Pythagorean triples:

In[2]:=

Out[2]=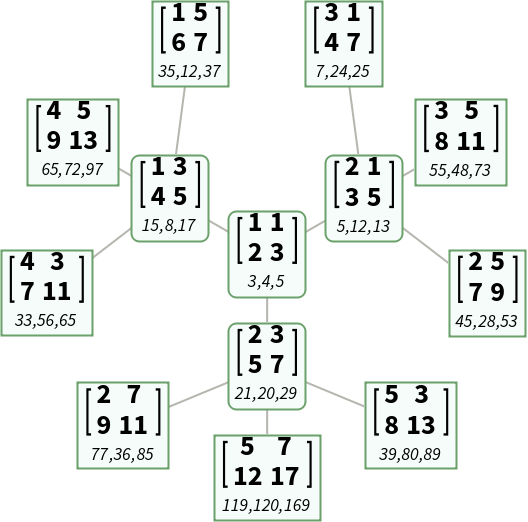

Applications (3) 

TreeExtract can be used to look up a certain node. To find a primitive Pythagorean triple containing 185, search for Fibonacci matrices that corresponding to a²+b²=185² or a²+185²=c² for some positive integer (a,b,c):

In[3]:=

Out[3]=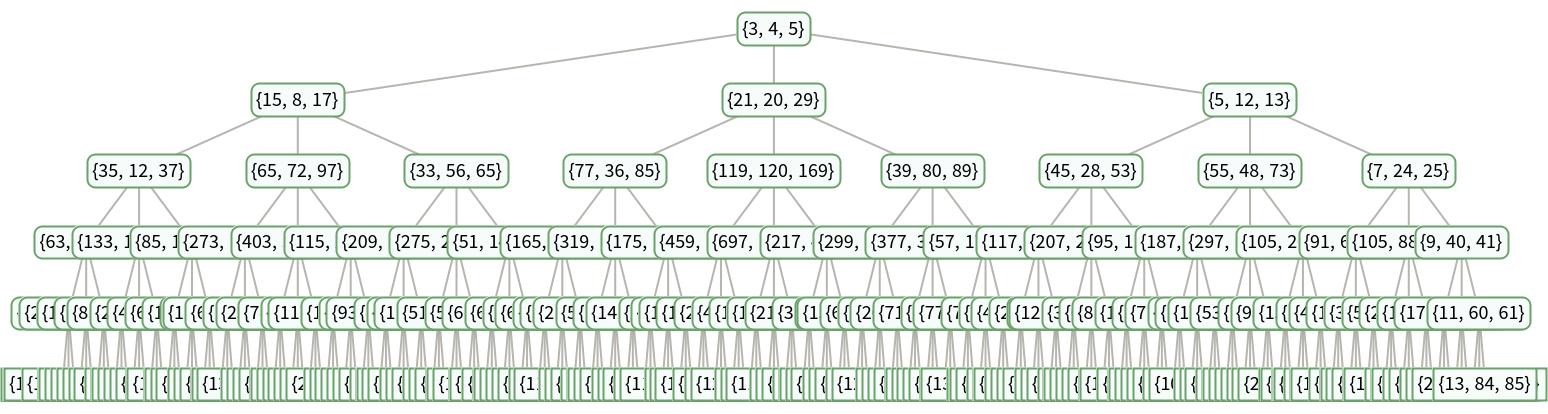

In[4]:=

Out[4]=

There are three valid solutions up to tree level 5:

In[5]:=

Out[5]=

We can verify the solution with Reduce:

In[6]:=

Out[6]=

Properties and Relations (2) 

The zeroth tree node is the root node:

In[7]:=

Out[7]=

The zeroth tree node corresponds to the smallest Pythagorean triangle with legs 3 and 4 and hypotenuse 5:

In[8]:=

Out[8]=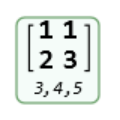

Possible Issues (1) 

A Barning-Hall tree grows exponentially. BarningHallTree contains a limit of 12 and returns unevaluated for larger values:

In[9]:=

Out[9]=

Neat Examples (7) 

Find Pythagorean triples (a,b,c) such that a<b<c and c-b=1. Some examples are (3,4,5) and (5,12,13). We can use the B-H tree function to find more:

In[10]:=

In[11]:=

Out[11]=

Find the corresponding Fibonacci matrices (notice that each matrix is the parent of matrix to the right):

In[12]:=

Out[13]=

Illustrate the path by highlighting the last four elements in the list above with LightYellow:

In[14]:=

Out[14]=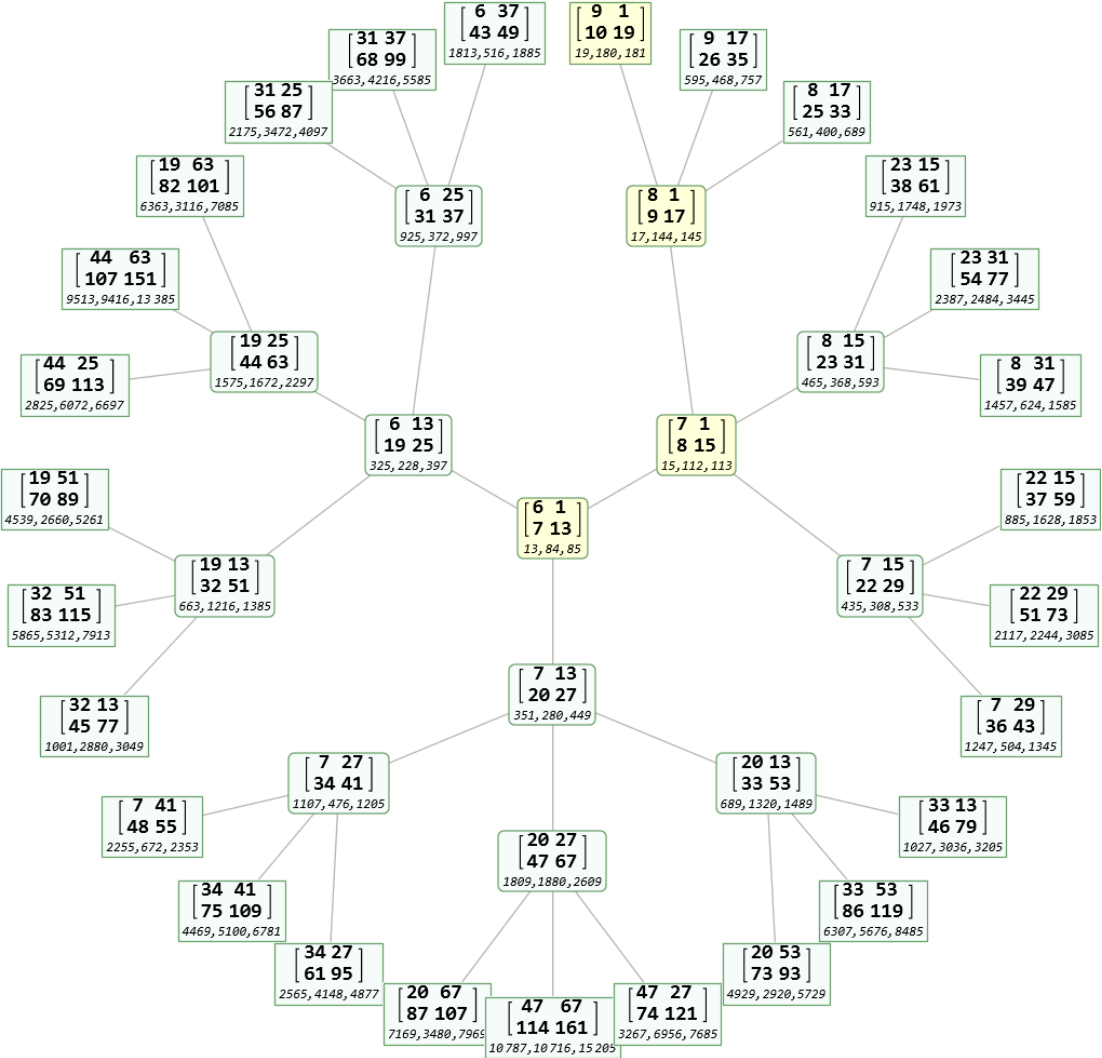

Directly generate Fibonacci matrices beginning with the same root node:

In[15]:=

Out[15]=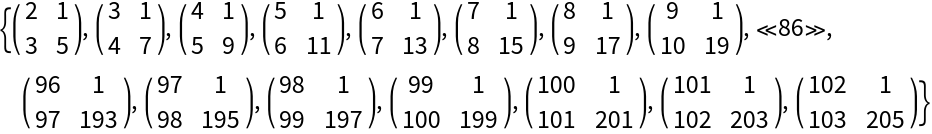

Compute the triple for each matrix:

In[16]:=

Out[16]=

Check that the results are correct by for a random triple from the list above:

In[17]:=

Out[17]=

All hypotenuses in these triples are associated with the following OEIS sequence:

In[18]:=

Out[18]=