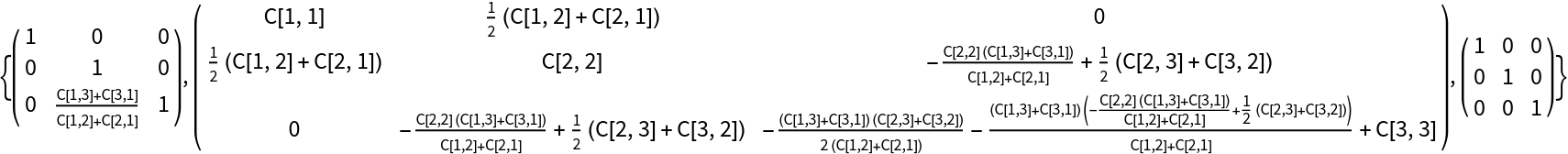Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AasenDecomposition (1.0.0) current version: 3.0.0 »

Source Notebook

Compute the Aasen decomposition of a symmetric matrix

Contributed by: Jan Mangaldan

ResourceFunction["AasenDecomposition"][m]

yields the Aasen decomposition of a matrix m.

Details

The result of ResourceFunction["AasenDecomposition"] is a list {l,t,p}, where l is a unit lower triangular matrix, t is a SparseArray representing a tridiagonal matrix, and p is a permutation matrix.
The matrix m can be numerical or symbolic, but must be symmetric.
The matrices returned by ResourceFunction["AasenDecomposition"] satisfy the relation p.m.Transpose[p]=l.t.Transpose[l].

Examples

Basic Examples (3) 

Find the Aasen decomposition of a symmetric matrix:

In[1]:=
{l, t, p} = ResourceFunction["AasenDecomposition"][\!\(\* TagBox[ RowBox[{"m", "=", RowBox[{"(", "", GridBox[{ { RowBox[{"-", "1"}], "1", "1"}, {"1", "0", "2"}, {"1", "2", "1"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}]}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)]
Out[1]=

View the results in matrix form:

In[2]:=
Map[MatrixForm, %]
Out[2]=

Check the decomposition:

In[3]:=
p . m . Transpose[p] == l . t . Transpose[l]
Out[3]=

Scope (2) 

A symmetric indefinite matrix:

In[4]:=
m = ( { {-4, 0, -16, -32, 28}, {0, 1, 5, 10, -6}, {-16, 5, -37, -66, 64}, {-32, 10, -66, -85, 53}, {28, -6, 64, 53, -15} } );
In[5]:=
Sign[Eigenvalues[m]]
Out[5]=

Compute the Aasen decomposition with exact arithmetic:

In[6]:=
MatrixForm /@ ResourceFunction["AasenDecomposition"][m]
Out[6]=

Compute the Aasen decomposition with machine arithmetic:

In[7]:=
MatrixForm /@ ResourceFunction["AasenDecomposition"][N[m]]
Out[7]=

Compute the Aasen decomposition with 24-digit precision arithmetic:

In[8]:=
ResourceFunction["AasenDecomposition"][N[m, 24]]
Out[8]=

Compute the Aasen decomposition of a symbolic matrix:

In[9]:=
MatrixForm /@ ResourceFunction["AasenDecomposition"][Symmetrize[Array[C, {3, 3}]]]
Out[9]=

Version History

  • 3.0.0 – 27 March 2024
  • 2.0.0 – 29 August 2022
  • 1.0.0 – 11 February 2021

Source Metadata

  • Citation:
    • Aasen J.O., "On the reduction of a symmetric matrix to tridiagonal form." BIT Numerical Mathematics, vol. 11, 233-242, 1971. DOI: 10.1007/BF01931804

Related Resources

Author Notes

The current implementation only supports symmetric matrices. An extension to Hermitian matrices is left for a future update.

License Information