Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the rational Cholesky decomposition of a matrix
ResourceFunction["RationalCholeskyDecomposition"][m] gives the rational Cholesky decomposition of a matrix m, given as a list {l,d} where l is a unit lower-triangular matrix and d is the diagonal of a diagonal matrix. |
Perform a rational Cholesky decomposition on a matrix m:
| In[1]:= |
| Out[1]= |
Confirm that lm.DiagonalMatrix[dm].ConjugateTranspose[lm]⩵m:
| In[2]:= |
| Out[2]= |
Hilbert matrices are symmetric and positive definite:
| In[3]:= |
| Out[3]= |
Compute the rational Cholesky decomposition with exact arithmetic:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= | 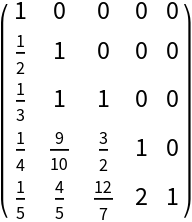 |
Compute the rational Cholesky decomposition with machine arithmetic:
| In[6]:= |
| Out[6]= |
Compute the rational Cholesky decomposition with 24-digit precision arithmetic:
| In[7]:= |
| Out[7]= |  |
Compute the rational Cholesky decomposition of a random complex Hermitian matrix:
| In[8]:= | ![r = RandomComplex[(1 + I) {-1, 1}, {4, 4}];
ResourceFunction["RationalCholeskyDecomposition"][
r . ConjugateTranspose[r] + IdentityMatrix[4]]](https://www.wolframcloud.com/obj/resourcesystem/images/610/61004a1b-552c-41f1-9b5c-18908c8b55a8/4ff6ebbc92a5019e.png) |
| Out[9]= |  |
Use symbolic matrices:
| In[10]:= |
| Out[10]= |
With TargetStructure→"Structured", a list containing a LowerTriangularMatrix and a DiagonalMatrix is returned:
| In[11]:= | ![ResourceFunction["RationalCholeskyDecomposition"][\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "1", "1", "1"},
{"1", "2", "2", "2"},
{"1", "2", "3", "3"},
{"1", "2", "3", "4"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\), TargetStructure -> "Structured"]](https://www.wolframcloud.com/obj/resourcesystem/images/610/61004a1b-552c-41f1-9b5c-18908c8b55a8/6710e662a9ae299a.png) |
| Out[11]= |
A symmetric Toeplitz matrix:
| In[12]:= |
| Out[12]= |
Compute its rational Cholesky decomposition:
| In[13]:= |
| Out[13]= | 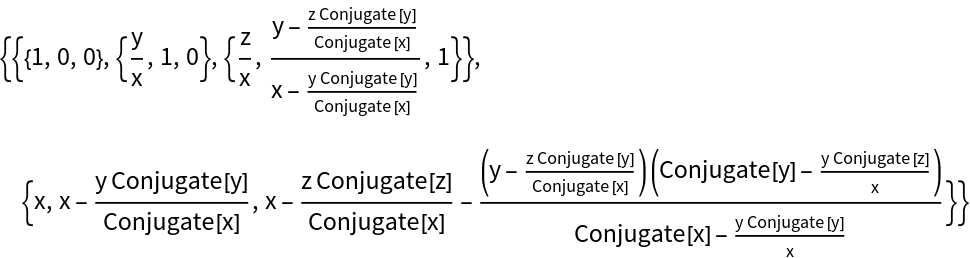 |
Derive the conditions for the original matrix to be positive definite:
| In[14]:= |
| Out[14]= |
Create a symmetric positive definite matrix:
| In[15]:= |
Compute its rational Cholesky decomposition:
| In[16]:= |
| Out[16]= |
Compute the Cholesky decomposition from the result of RationalCholeskyDecomposition:
| In[17]:= |
| Out[18]= | 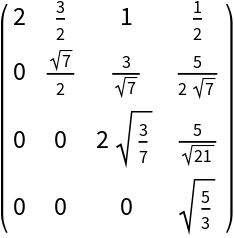 |
Compare with the result of CholeskyDecomposition:
| In[19]:= |
| Out[19]= | 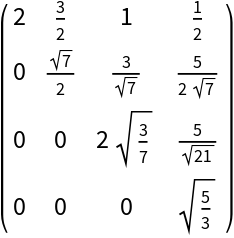 |
This work is licensed under a Creative Commons Attribution 4.0 International License