Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RationalCholeskyDecomposition (1.0.0) current version: 2.0.0 »

Source Notebook

Compute the rational Cholesky decomposition of a matrix

Contributed by: Jan Mangaldan

ResourceFunction["RationalCholeskyDecomposition"][m]

gives the rational Cholesky decomposition of a matrix m, given as a list {l,d} where l is a unit lower-triangular matrix and d is the diagonal of a diagonal matrix.

Details

The rational Cholesky decomposition is also referred to as the decomposition.
The matrix m can be numerical or symbolic, but must be Hermitian and positive definite.
ResourceFunction["RationalCholeskyDecomposition"][m] yields a lower‐triangular matrix l and a list d so that l.DiagonalMatrix[d].ConjugateTranspose[l]⩵m.

Examples

Basic Examples (2) 

Perform a rational Cholesky decomposition on a matrix m:

In[1]:=
{lm, dm} = ResourceFunction["RationalCholeskyDecomposition"][{{2, 1}, {1, 2}}]
Out[1]=

Confirm that lm.DiagonalMatrix[dm].ConjugateTranspose[lm]⩵m:

In[2]:=
lm . DiagonalMatrix[dm] . ConjugateTranspose[lm]
Out[2]=

Scope (3) 

Hilbert matrices are symmetric and positive definite:

In[3]:=
m = HilbertMatrix[5]
Out[3]=

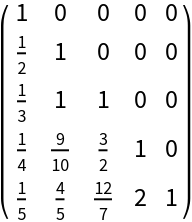
Compute the rational Cholesky decomposition with exact arithmetic:

In[4]:=
ResourceFunction["RationalCholeskyDecomposition"][m]
Out[4]=
In[5]:=
MatrixForm[First[%]]
Out[5]=

Compute the rational Cholesky decomposition with machine arithmetic:

In[6]:=
ResourceFunction["RationalCholeskyDecomposition"][N[m]]
Out[6]=

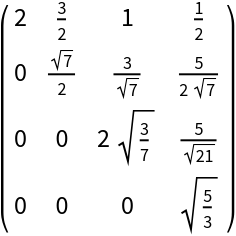
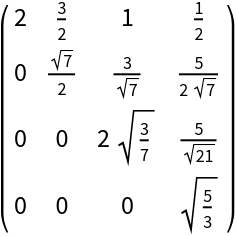
Compute the rational Cholesky decomposition with 24-digit precision arithmetic:

In[7]:=
ResourceFunction["RationalCholeskyDecomposition"][N[m, 24]]
Out[7]=

Compute the rational Cholesky decomposition of a random complex Hermitian matrix:

In[8]:=
r = RandomComplex[(1 + I) {-1, 1}, {4, 4}]; ResourceFunction["RationalCholeskyDecomposition"][ r . ConjugateTranspose[r] + IdentityMatrix[4]]
Out[9]=

Use symbolic matrices:

In[10]:=
ResourceFunction["RationalCholeskyDecomposition"][{{x, y}, {y, x}}]
Out[10]=

Properties and Relations (4) 

Create a symmetric positive definite matrix:

In[11]:=
m = {{4, 3, 2, 1}, {3, 4, 3, 2}, {2, 3, 4, 3}, {1, 2, 3, 4}};

Perform the RationalCholeskyDecomposition:

In[12]:=
{lm, dm} = ResourceFunction["RationalCholeskyDecomposition"][m]
Out[12]=

Compute the Cholesky decomposition from the result of RationalCholeskyDecomposition:

In[13]:=
DiagonalMatrix[Sqrt[dm]] . ConjugateTranspose[lm] // MatrixForm
Out[14]=

Compare with the result of CholeskyDecomposition:

In[15]:=
CholeskyDecomposition[m] // MatrixForm
Out[15]=

Version History

  • 2.0.0 – 27 March 2024
  • 1.0.0 – 06 January 2021

Source Metadata

  • Citation:
    • Golub, G.H., Van Loan, C.F., Matrix Computations, Third Edition. Baltimore, MD: Johns Hopkins University Press, 1996.

Related Resources

License Information