Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a normal texture from height data
ResourceFunction["NormalTexture"][data] gives the normal texture for the height data data. | |
ResourceFunction["NormalTexture"][data, s] gives the normal texture with relative strength s. | |
ResourceFunction["NormalTexture"][data, s, r] uses a kernel radius of r. | |
ResourceFunction["NormalTexture"][data, {sx, sy}, {rx, ry}] uses separate strengths and radii for the horizontal and vertical directions. |

| "Sobel" | binomial generalizations of the Sobel edge-detection kernels |
| "Gaussian" | standardized Gaussian derivative kernel |
| "ShenCastan" | first-order derivatives of exponentials |
| {0, 1} | the {x,y,z} values of each normal are rescaled from {-1,1} to {0,1} |
| {-1, 1} | no rescaling is applied |
| {min, max} | values are rescaled from {-1, 1} to {min,max} |
Normal texture from a grayscale image:
| In[1]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/0f768bf9-b691-41da-b7ca-9127f1bef91a"]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/416b83efa7120c00.png)
|
| Out[1]= |

|
Normal texture from array data:
| In[2]:= |
|
| Out[2]= |

|
Normal texture from a height map (CC0 source):
| In[3]:= |
![ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJxsvceWJFeWLdbkiEP+Av+CUw45fVycvPW6UEBBA6kztHKttZm5ubkJN+Va
ax1aR2SkRCYK1dXNT+E+1zwT3Vx0AAEV4WHn3CP2PuL6//bNk//2/f/8L//y
Ly/+F3z5b19v/B/Pn3+99X/9r/iX//vxi59+ePzdt//n45ff/fDd8//9G/q2
f/mfnL86FcMql8u2USqa5VZvNJ5Mht26aaj5nCjmcjkhJ+VELp5Jp1PJVEbI
CpmsWe0Mp8uj0/PL65vrq4vz05PlbDIadFv1sqnJIpfheIHPZnM5SW1OT68f
3n38/R//9s9//vvq9c9//hte//gDr7///vHjbx/evX51c3E87RYLmpLLieX+
/OTi5vb27vrieDbsVMv1VqvVaNTqtUar1e60O82KLnPpfLUzns0mw17VVPNW
ScdvzuYkWRMFxaq2+qPJ4vBw2q8WxHiswB74+PT05Hgx6VbUdCIRCwcCPo8/
HGrYtqZZpmkZ5VKtOxxP5/PJoAE5BFHkBQ4Cp1OZVDrNpVLJZEbgRYEvVNqD
8ezwGAq4ujw/Ozla0GN0IL6tyyKfTqTSmUxGkCTJ7C4u7t58+PTHP/7t3//9
T/mhgH/844+///3333//BPnfkvxHkF/X5byYLXYmh2eXV9dXZ0czHEW53Og0
m41Ws9kdjUaDXrfVbFt5rVAfLU/OTo9mg3bJrg1qilaQJDlvGLKiFuud4WS+
PJwPW3aOD8chf280Pzo5OT6cj9plOR6IhIJel/vA5fVWKqZeMTXDUvVauz+a
zheL6bCJtxH5FM9lcI5ZPpNOJbhkPJHIZAUxL0p2vYv3hwLOSHqIPx72u61G
tWSqkgBLgQLSGU6SleLg6PJP+f/jT/FJ/j/+/ukjHf/7t6/vIf+kbRcKaj6b
s5rD+dHZ+fnZ8XzUa5ZLlXq1Ums0mgMczXw2Graq7WqxWh8dnkNH50fjfs3u
dcxCoaBJeVkzjJJdbvRw3svFtFtW+YQvoVda3cFkeXR0tJwOmrYUDQR97v29
3Z2DgwPbKsF41IJtmPXeYDJbLJfzUQvmn8WJp7lkmhMyqUQikUzE42k4g5SX
choUDAuYL4+Oj4+PlvMxTr/dJPFzPE/aSqbwszlVKw2PLu/fvP/0+x+w/3/+
+z9XwkN6Ep8OH+K/e/Nwf3V2OG5ZBUPL53JqrTvGWx8dzsf9drVUqVaK1Wqt
MZwfHh0fLmejQbs/bNT6hxc3d/e3l6fzbr1oNUzd1BVZUdRS1bIqrd54tlzO
BnU9lwy5knq1DfnnEH8x6detXMTv2d3DHztbm3uKqCmqVlBty6j3RtMZvGY+
amqqjINMkSDpTApHn0wk4xlZkSTSABRQa3X6sIHFfLmYTUf9TrNRtQswXpHP
8KkMHCyVEjW1ODjE+b//+OkPpoB/rs7ecf3fP31yxIf5X54syOkKBVmrqla9
M5rMphNElGoR518rlav1/vzo9OwUvjYZjIbQweLi9v71w/3N2aJfqzWalm5W
ZUVTC5qtGTDk8WwB6y/mubjfnYb8eFhIhqPq1XQh5DnY3t7e293e2t5DeMsp
uqrIqtXE8cNrIH9d0/JiJg25cZD4Go8n0slESszBPCnK5BSzVG20uv3haDwa
UuSrlgxVzYsIlek0lEbfn1Vlq7c8u3l49+Hj73/gyJ2DZ0dPvr86fXj/3fX5
0axfK6gFVbOLtmbVWt0eAkqzatslHH65Um1Mj84uLy7OTg5nvfF0NBuf3Ny/
fvvm4eZ80W22EXoqrbaRy+UN01LNGuLTdDpqlxQuGXK7mPwjHBa5druiZnwQ
fXdne3d3Z3dPkPOSUpCUvFxuD6ckP+ymgoMQ08lkPJmGN0dj0XCMXCCNwC4i
sOclVcnrdhl6b7fbzXqlaBVURdNkcpokfixOiuPlvNaanVzevSYF/P2PP5jo
K+EhPbn+e4jw6vb68nSJp5VlmL9cUPi8UYTVVypF3SjaVhG5qdpdnF7B3a/O
jme9wXI2Pzy/e/327VuSv9PuNipGqV4xFRlekJMtCmTjQbuicImYz+PmIH8P
FgVrnQxaJTXlceTf2t3ZwflLgiJl5ZxaQZJYLJaHi0nPlmHLAhRAgSwRhQJI
onSaF7KiIGRzioIoALUZtm1Zuqaqqqbhb7LEpxLxWCSaikJzHL6jMoQBvHr9
7rffPn76ncnNZF8J/+7tG5jw7fXFyeGkVzMkFe+gGIUcL+RhyDgDSbdwoJZu
lIdHF9c3tzdXFyfz4QCh7ezq1Vsm/ylyRKvZKCGB2Wa1oqtZ2a61e/1eu6zx
0VjE7/JmDTp/nO18Nu417HzCfbC/u72zubW5vbMn5cV0LsvnspTVSP7FDOFP
kXHUiP4Z+isVi0ABiXSK5Bd4Ht+t46TgOHjJyLkF3ShomoLQSD4DbfGJCJIl
L6lWe3J8AUt98/4DVPDxE70Q9D8g6ZPlP9zd3d1cnR8vp/2mLYt5ZsCqIGZS
Qg6JR1QM08CfplkaH1/e3NM3n86H/dnRIeR/8xaJA/8+7tabjQbcvmghjyMK
Iv132vWSlo37/d79DU/OrHX64+mM0EK3ZuVi+/sI/lvr65uIAXKWo2TFC4Vy
qz+GiUxHQAh5AWJzPBIgJ/DpeCxBFpDimfzQCf4GK5BVOnJZg+waAoiE2JBJ
xmPRWDwOk0nwWZhVuTc7vri+e/X6zdt3795/WL0gOx393e3N9fXlGUBJv1kC
cBHFtFIqQKWZrIhcJiHLQ7W6VtCLoxPI/+r+7upsBghweHJ6/Qrv+XCLvNlp
1Gq1Vk1Sdc2EupQc3KVWNhUh5j3Y2tpe90t2ozsYTyA/nKJqiOH9g/2dzc31
je2d/b08n0myfF0oNeEkk/GgWyvkBGg/CenxgrxiXoZpJxNpAY+YRXyn/4xv
kfN5Oa8oiozEgzCCn+FSiVgoEo/F0rEUx2XFrFLtUeS6ub1/9QAdOK83b17D
7mH4QI9nwCSwyrKhCBJcTjQLVVvKCDlZ0Yu2jUgD7RZsu4d0d38P+U/GvV4T
Cji7vrt/dXd5PBvUaog/FpI/eYteQDg3LVPLpcPu3S28XoblYoOA3YwSVatc
EEL7bvfO5sb6Bvzfhd+ZAMBLptVio9MfDHrtqo48JiD1Z8gI0ilBNexSCSFO
4lLAg7IocDxMI5sDFkQuyAPnQT/5vITQyPHMAAgtpDOAC/mcUu0Cep1eXF3f
4oGdFwlyu4LOR4hJnXpRk2RgbRhcHqYnpLNQrFyvFwDBgedU02jMT69v7+9u
Lg4HCLjlznh+fH55ibTRq9cqtqHDWAD+IL+BBIVH4RIh187m+tray5cxFSc7
pOOfAE+VVC6473Ltbmx747m0xy0C3mQyyVgiZxLQbjarBt6J0hiEFQQuwWt2
pd7E/6mXLUXk+TxQgED2IQg8xwmMJDBYkEMYIe9A8ifAAPTAQwFZudjsAc+c
nJ1fIILf0Avnfnl5Qdn8cA6XbFYtsA0Z+iPikExyfDpL6igXcQ4wOeSRgj1Y
nl/f3lyeTrutWrFkVTsANECD3WoNz2VQ8MmJhqUrCsI2UnbI79leX3/x7PmL
9aRWQfij6Af5GyU14z/w7O/sZbWskEvHclmBg52nYpwCIlQp2TosGtbOE4fJ
iTkub1Wbnd5g0O91mrUi8qKkqXk6JdgAxQeEqRwDRdC6AP0QboolUklAIE5g
VgL4ScAa8O3klHDt2RkxkaNDQk6EcWwD2cfQoVSOhRxeiCfFHP4FvsZTvM3r
eqEyOjw9v0D067XKuiwXzBLoEAGEcski+JLjOaWgShIXjwQDfu/B7s76i5fP
nr14tpUpkLIc+bt1W0l73Z49n65FPfsJPpmHAiAKl0gISGhI41JelYn7sUwn
yVm13KToMaHQ0GtD2UjzCtgBDwPniCCJJD0CoUMX4R1kO8iDqQzHEX/K8LJZ
aQIuwgUJgyDFLBYwxjFxmQZleUlChFFzZG6AzwxmCIS603gyqFRQge7MKoO0
42GnZikUgZF3kC81vcBCr8Cl+ALskgv4vMhuOxvrL58/ffHi2bOXe4JZ646I
OyC09+q2nPT7PPuelGdjfdcTiUN+PCJHYD+Nh8VpAgvRcUIDWTJDJE+gqRme
eT6dDPvtesUGOITxZ3DQAr5NxE8oiIRqQQcGUEQERw65kv1BDBLfKAAtAS92
ev0+QsxgOIQ1dduNWrlomIVa1xJhOSrRTUp8ecTvarViF8Q0RdlcPg9oadR6
Y9C/8aDTQKaIh+OxcCROhJQSJVJUIhFNZtOJZGBvb29nfe3F82fPnj55+uz5
83W3aDWQ2Jb0/CR/Ph70+1yb65ubnpA7EEHOJYaXySDFRcFwHHPOklj4Iqma
xcge8ZHDQ2J6PTAdW4WrZ4gf4ezh+4AtumUX8bKMQj5L5wiNInFmqBgAKThe
hMkWQWZqcNg6uHy1DOhUtDTQlVpZEzkeJpXJZ1OSUWl2Ad9G8FULAYEXJVGr
dTv96RivQRsuKKUD/oTX7XYH/MFIJJlJxIFPQsF4Ohry721tbKw9e/Lk0SNI
//TF+ta6Ty62AOyW7Ol7NUuKB3xRPyxk+2BnM5mWYP8wAMC8WDwaSkFmijnQ
ANJRDnxStRq90WwJ5z0+Ia7HqH6jYkpcOpkGyUcokHL5ggWOQqdWLtkGTABu
DLSUosSa5pg5Zzl2lCoMtmARWzVtC9AOWtMUTcllUjlEIV3M6gRDZiuuWlcR
Y2S9M8PDT8A1+s2areZSgf29fdfe7u7+nsvrC8ajQXi8x+0Lud372xtrL59C
+kePn7xE7Hu5+TKkVtojekOH/ZhSLBAIAQBvrFMBIIHTQxojW8bTJjMQOgfw
aZmM6hEMhfz0PMenpxS1DmFF41GvXbPy8H64vgIHypvFSq3eaDRwshXYtELe
ARbIXABQgUKaKMDQoC+BGC7YRhZIT1dKFdMCbVaziawIxiimAN47o9nh6Rm4
DkhBU4Fuq7OT8/PTJZBJo1TI83H/3h6g6+bWxubWzoHb5Qv6AkA0e1sgNLsk
//Onj589f/oUhkAZMFaotkcL6JMR6oYlRb0+F5jv+tqW1+sO4fxy8GLy0mSa
R8LOibJdrVetggifxmk55390AvERt2ECYBGjQadm5zlkJkmWxZyOWIwM2UaS
bFA61iUuh/fDgSISUhQkdyDayKoHIn5IBVPXlGxlACcwLFnSjFIukcynOIXJ
f3QGvABkeDiugQ/2ji+uLs+Opp1asWwmw26wNlj51sba2sYW/nnP7d3b2dkm
OL+5uQ1Yu7Hx/OX61tba+sb+1uZWQq92Jjg/Kv5MIH8u7HZBTXhtH7hTCTlH
sDtLqYbFOzmXtRqdTrOi4PgVDTkR/j9dAHGe0euEmQDCQLdhiwLhHghTRGxr
tzsdkEHSAAIksgJEpqBKDBphDVkdjoWcApyiUKGioOZkrWwVbLNYhswANcVS
Lp5Bqmj1p8vTi+vb29urs0Wv1mpNz69vrs6Ww3YZ0TLoP9jZ3ibxX74Egt/a
2dvdd0Mfm5AbfxHi2wa5odrGJv6+s53Wa73JEqn3+GhB8othjxvQaGNjfX/X
kwoXVcQ5WD2FO4kkzhWa/eGgUwWgxCHppWK5PZgsDo9XCmCZe0lMom6Isgb0
m9fL9WanC8be7eDVQlg3c4LEc4gPKUoFINHIhhxlTJ5UpipIWTAusH1dkxWj
3gUKIN/RiVmV6p3h/AhgB2zn8njc7nYPr25vCei2ipaUCPpc2zjazc2NNZIY
DIaY/BZC/hr+w9rm9sauywXPhgZ2onHv7i7JPyX5T5j8Zjbo8hzsbGxCPa5E
MNoHIQTZwJHI9Cqo+Xp/DKBUNQuQTbEgP9LHlAzIkR8KICeYDjsVDS4M8msw
+Sm3QQVdKKBqK3CprIDjT2UBEzJJUAyecC1CBgiTohUUIrsIh5S883qxDiBQ
LFgqx7BCf7wgA7i7BdwbjsenN/inw2m/bmhCJOhBbsfBkwVs7+7tuvZB5MFj
EQr9Ab/f597bdXv8fo/L7TqIpj2e/RSzfyr+Qv5e3cgG9w/2DvDD2xu+WIhb
jLvVAjH4goZjUQt5q0dl5V7ZMMDqjCLMs0IGsPxiACvwNh3iPIhw6Ih+9RZB
xAGhxB4UABInER8A9hEI0RC4IBwHRpQjpABeB/FB9fGbqagmCIpeALg2+aSg
gr4Ppodnl9fX12D70/H0gjSxHLTwrlwq5Cbj38Xxbu8d7CIPuH3BSAwmxlOA
yYHNhHyIa26Pz+uPRyJhV6JQaTH5GdGqGXzoAC4DJ9rZCkaiacSVQdM28ERg
sfiqNIgET3pFkAkNiQDcp+hEgM8KIB9AFABnr9mAywV8k1WuEnkaAtgwnFwx
VJlAZI4wFCBAGsGQnB+4ns8h8gEmafg5g+lBAsjKIlimUkm+Xs6IGn4fhcBL
8JsT/JrFNVHFY1iknE1Ggr7d7e19j8/j2YPwvnAiAyKuaLphFUtIvpYuZ9Ox
kNftCgQC0Vg6HY6rxTb5/8mxU/1Lh1ywEdfO3uYerDJwdX48H7WsggnurOum
bveR7OeTtmXaJVUxDIM8AAxm9lkBDMBDBYeLcbuMWA83AUe3y/V2fwiENiQK
WaP+CRQATEygOMuBalDc5/gshRjSM8ArbA7aUzXEHoHPK0AK6bwlyrJWanTH
rNxJDYvpMYjvzfX5BMRMSIb8AfeuK+gPhnwHvnAqm9dwQOVKHfmHRWCwNKpC
J4KeQDjOrI6XrBYY6PHJEdAzwloqgnfYOwD62eNEv+sORrYY1Q3Ttk2joBu1
8QKJclg3jZKtUV2HGEa1TaURxl8g//kF6QDm1K9XTEMBFJRysm5VSAHAaMN+
t1EsMFwuEy/O57MZgokgspQBEflVg+o0efyTQVrA9+TyiI7A/ZkULymSbNdg
cTDDOSjS9BTyIxIcDYG54oFAMODzpRLJUDAh5DWzDBbU6QJSM4YymYwA0Is6
8FQ0EAeoTRNHNxrwpyPHZUtq3Bs8IOfxHIRCrr3QAzj18bxXtkolGLNudZDr
D2e9smmVbd2CPVStUqVMFVVmAST/Bb3Oz46X41bRkIUMlTuBbArFRm8A+Udg
tCXL0llUUSmwShLyhAqLoDohor5ZtA0DdgM0SHGH+K3MJZPJNHAy8L/IZ7VS
rd3p9ofTyXR+Bt5/e7GcjJs5Lu6DXYdCCfA1gWrQrd6QFTYXrBVB+HQ66jcr
eCw+FoP8qXQ2ky5QCWJBWbvXtPMRn9+1t7N54PcFXDv7gdfwrbOjSatUKkNg
ozSkNsEYZlQsmlaxUoVW8LdSjVApUAAxWEh/CQWcHM66wGNcLOQPh8Mx2CIj
ulBAv1WyTXBWqoshpuKLTOklRywPWtEsw9BNmJsB/EvfVtA1BEueo8p5msCY
kIWJkNUNRuP52Q0y4cWyW61ribDXG/CHolEACLtKTZ354jOtpociq1xQRaEC
jphg9atsJiYVm9TZmE6A2oxs2A2CuLfj8fgDngO3//XD/fXl6aJXhvwly2yM
F8DJ/XqrhjOyiogo9UoREaBSczg8/S6S/5IMYN6tFFQh4jvYP/B4gwkub5Yb
3cFo2G9VAO4RTnTqSqmGRkYAZ6cQVanUQICaTaqc06tFNRfk/mqFeLyUJcoM
SI3vLzaR+3vDxenVze316bxjStl4COYfCIeThk0tTWrBscfBd9Dr5vqKzBI0
r1Ux8sBfiKrpdCSNDAA7GQ16zZKW8cHy9w9cB0BBXk8g9eb1K+Csw1EdshaL
FaTKw8WoVauDmJh2pWgVq1a5ZuGhy9TzQhpAXDpDADg/Oz2etYuakIQZEQ5x
BxN83izV291et1EpUTghFRgFROeCRSEKjtoj8ktBYjKZTqkii69TKi2MhsM+
tVArlpajzjFgklZrt5ud/gip8PL8cFTTshmE/yBUkFaLrQEwzdn5JZWUWGHt
4eHVq/u7O2gAdkl1rkI2DQjKp1PxuGRSCQdvXzXzcUi+t78PiOSCLcXFN6/v
767Pj6etKtl6rTudz6fDQbNRpfMvlYp2uVjREQIqtl1pdFgUIC7AMsC4UczH
QwRI1jYOXO5gnM8DvoEI1OA1UIAFI6DUQO2cPoAM1T+WIKLgIoDjJ4xR0Ys8
F6Bywbro4JYKFfNUg35ro9WdHJ2cHE5aVh6JLewPBYOcVumMF8fUfr+7u4fs
r1+/YS/YMjDj+Snid6duSVSN4qm6Da5FvRoAcyr+HQAub+4euLb3vGFOeYOf
QQqYdeoVGGG9Dz8Ztjv1erlchEkWbZhFFWGxXClCIcVaixop5HOAQNNuWU6F
vPtb6y9fbm4f7HtDCU4qWBX2w7ZN1m4XSWkj1lY9Wjkq0gf85wpHh9e187q6
Yh6FHD0bMZYnI3/oCEClahPoazJslHSJj4eCIX+ILwDQHwIg4thf0+vt27fv
6fWOmkn3t1cXp6DO7bImSlSJyIDTczkQdMQkNRtzHxy493cBnDzufX8sq+NH
HPkrFWCYTn8yHXUa7WbJLpUq9SYMuQ6CqlvsQEHai5TnR4jK8xmbJIiCS66v
PV/bAgsLRBLJjJg3oKlSkZyJunKIPIiox47gl5dM4huaboCx3tHxfXnd3d3e
XOHwZsN2RZeR1w38SrtUR25vNmqWmkOkDYcDXKHamx2eXd28enj99s27d2/f
vX//4cNvv32gbtpb6iddnR0vRt2aweCXwHNZ4nbIMWpeiDFkfHCAwwr4vIFE
zni9kr8LcTvNZm847HQazVGrjFetUa6VjVrJtBEHyjbCdpHkKtXglv1ei5rr
wf2dzRcvXqyv77gRAsORVCarIs7RT1cblXrPmZMgwemYWZhiQj/gxQ5vZbrM
fNnDn+Ph2xUES5sUWSlVYU+gVHpeyCSisVBSrXSnR2dXt69w7hD9/YffILzz
+kANNSbOckLySxLJD2rPi6xonwqHwiGfm7DvbsDj8XoTkgH3x+88mbZLFgIu
ole72mzV2s1mq1pu1OD05Rr5gGkWTUpaRTJqRDarWNSlTCLk2treWNs+8ARj
KY6mA6hqolq1KnXsG8Ady5PTi0uqejuSk+iIVSQ264bg+N47rw9kwDQKQHBk
0IABlciMKsg+UCWFRS4dj8XiEtDs4enVHcRnB//ht48ff/vtPftKoxSvAWgu
TwicFwA4s6xhlQIM5OLRRCQUDft8Hmr+bO64Dg5cUVF/dXdDhYZJExmrgvOu
1yqVbp9IHByiWqy3OyXqwVkm+2pBborsAPA5PhUPuXc2d9wEQ+EZVacEVEHc
qyKY4t/608PT88ubG8fMPwv/QI0gaoe9WwmAv+jp8Rebhbg+Pxy3azhy26Zf
ZuEP6F8V+VQ0FuOMJjLi5S0T/wNrKn5kLUU2SvLhHY0E0DTBpFcB3pKI1fMp
KkXFw7F4NBoBOXLt721urm/u7O/tBTiNzOX8ZDGsA8mb+FXI0OUmDRl1mtVG
vVrpADMY8EUooEjtRYrpOrihIkB83/aWO5zJF5Aa2siw4wmYM8H/Cp1/HbmU
0di7V3++mNW/oYNnh06m+/HjqjH66SMEeEMGMOk0Gs1KGWChaEELlmEV5Byf
jMUTCqyfdVS/iP/J+WH2Nh+on05NwsMp5Fc1mSryrI+ZgvDRaDgU8B4c7Gzt
bK6DAu7ueRN5Zv1H816FwbWCSWXcSqtRrw37jU4DSIWYOZhVuWhSxRJ4pkBV
ixyfxunv7XjjWc1GVhg6SMwZhwEGr9aqjf7sGGEKUZqc/bP4DyxgO467Or3f
Vy+ahXr/xpkFajZr9SYSEpwAegeIyouZeDIpGPUBANHtqzdvmPyfNbcyARYB
YEEXx0Dw1BoABYXjI/6lk4lYFOTRi+C/vbW9ubG2SdMPIQHecnq8nHRsYqWq
BmZiWb0ufnUTVH7QrTWA/Og4qVSPoyDKXijkRS4Z8Qd8JH6hRNNGCxbmGC48
PaK5pVqtNZgdn19/lv/hT/Hf/P+Lv5oFu78+W44BC+vkTrVKjcrqpqbkc+lM
OpkvNseH59f3r95QN5n5jKMCsgMWCN6xaSqapgOZLVAbQ6D4T+0UKABBn2qF
WyBA+LK/40neXF8AMo6aBmhKjrqteqG3AAppIB3Wmr3puA7sR3Vti1RDxqhr
qiTEwwGvz+uJCBpYz3gOLHZBSOyW+pqXp4fTfgtYYsLKWI7Pf5b/gZn/F9P/
9PtK/k+r46dRwFkPYRihpNao1htlwuWsOcil0kj9M5j/3QPpkN7hw/sPH/+0
ADZQAw2e0zQZnJWoZZ4Kz6LIE8GKR/3eAyhgy+fe2trcOdjdDV6R/PNhDSZN
w22gaVqzXSb1Aw3Vm9PpqrLVBTitlulNDVXik0EfkUh/WraR4+ZHJ+dX1OIm
AQmB0DhPo9oczvGst/d/tn1ffZb/7bsPX4LXl8eH9b55BaaL/Ad+QAXBVqNW
AwislmRBzKa5jGA2R4sTkp8ZEclPkyX/Vf6Hu2uG522zQBUtJSdK1NER+CxN
cgS8bpAVcOA9GMDulhtGe3YEb5Goe0vNL5B+mFydep40DjBdUM+OeocE0BsV
CzaVTUX8B9vrL3YjWb1K5XoSH2HO6fBTBro4mvYatfZocUxjKxD8M8hhye/N
Gyf+fQl/Hz+PQt3f0ChQB+qHBlibiNpF9UqBRxwHMSq2x0vID0VSDHU8gJT4
kd7IgQBvHmgorl8hCkr8O59zmtPwgSSs1uMGhY74gu7d/b3t7d1dcljkG4vA
Ik27ygXKAY3u54DGAPrJEev80JxfvaQJqbDPtb358rk7KdtIcovjs0sGRulc
KYm/fnVzfjhp18qt4QxQ5fr6dpX9Hbj+8PrhzWvKf+/fOXkfP8OQC1nOyXzc
63Q7BPoQgxqtVrfTAZbhCchw+TJyygnNkzywIPqnAj8jIBz/q1u4f7sKxG4U
NKq36CZeekHJi2BDsZCXeF/4gHgAcsAlmf+gUeAEQZRgAGoB3JImgY7+c7GD
qodLaqCCQpu5hH9vY+3ls3U/p5XbEPEUBPSejbi8JxT67h0NNC4HDRvEe3J4
4qA/hAcWIEgJXxLhZ97y6tXd7e315TmAy2DYBw4FW4QHtDudQX8wApgXM5yQ
SSvET8nY7pmpvXPQHwXBlfSwIZj/+XIIXy3bBoQG/aqwCFYi4KIrUjYV9e24
Qm4PJUDXwQX9zl4ln2JdZ1HMyyaJvwRiZ3CdnpwG706Pj5cLUMNu3crFvVsv
nj19vB3OGjSrSd2aOzbis4IzgGG3V0jiRb1YbQ+nhw76Z+nB4TyAg3crIEz6
uFnNghzOqSc+6DSRdZsgv202YDihtr2MLA75q10ifleraZoVgnLCACMANE14
e3ky7dL0HCK2bgLRQZFEIQBpG42qpeWFVNC1Tzhoe39///zsaD5u2zTslmHz
bYVKq0/14nNH+hvC7SDgpIDDhTM/GfXsUo91JyZZiH4wf0I5eKB3n4kITXSf
zfslrWBQlQb5gWGDE0Z5WQ3V0YdTSHPeejYZUv+ghaesVehh290BhJ9O54vZ
sGXgbDJpleQ/OndABdjPq4dVIF39WgLQQD/LEdArUVDbAodBIG33BkNWHRz2
WlVLFdMR967Pd7C3t7d7dnw469e0dCoBeJFO84pTfT4BZ1mNq9ze3Fw58oOj
E67KhFzbG8+evDiI50n+5Qnc37H/1WGwIHSxHFRkWQWPBDwaDBFLqd4xozkE
NgXBXvPZlGofVPpoE2Rod1uId5VKq9npDCc0drCktjuoJjX502q5PWbRxjGA
1/evV3F0FUVAoe5vL5H8AWIZBS1Va7V6azCdLQ+pxsD6Vg1wKS4GBbj3gYBO
jpBuirlkMpFIxBPJHKy/P1nApS+ZnRJxgfxX59T4oqJ/t5RP+ve31p49feFK
5O2Gc/50IqucTPNtdAyXR6OaJOV1SzXBqGB67XaXOoSsTehUvpoNfOk06WFL
iPU19m1ge/ieTn8Ijk0V15OT46P5sJHjIL9SatKvgwPcvfoCpN85sr9nqefV
7dXpclgDYC0Raa2Uq4jByyOaPqL6AtWAe1QdFGIuOP/+3u4RNZb0TCKZohG/
DBvtduS/vL5eiU9zaqQA0lXTEmA8Wy+fPXvuSkJ++P8hUbw7lpMcRuPIfwz5
s1m5oClmsViuIpjXmu0xq/VRsbFC9VbbpPHmatUGxSvWOgQ5cF4AHCNkVco+
5Cynp0gmmpDlMmrRmY2/vGWo0kmkq9dbFkdplBjHD7humZZRrNap90ebGuTI
F2e0qTHoNMqmwkf2XV5EgOVs1CnnE8kY0GEsIQLNIvVBftj/qlJB8iMAkAIA
aypyKri/vf78+Us6f7PWHYLhn1MAuH9YAXsqxCAJHY5qODQoIK8WaFS2SKod
sWAMgkQh2aZjgpGCYbJqmU111lqrD8uHwZ5SjKBC0cX58bxf5Hk+pRRxmods
8QS/jkGpP2cKmfjE/YZNNjQMvtKAKUP6K/r2u1tWG6SBs1atpEspr5umpGj4
0ORSSXDDSDTB2q8Ur1bx74ZMgKpTrOJ5gnOwxJgP8j97/vLlfpwNB0FbSBVM
AQ8M2r0lDnKDJFTJImkJkpinRkXJ6tZqtaJllZhzwjsNkzi+RZ0noG4DeRpM
t9piqwWUflj4vaH0c7IcVYS0wCllkIrDE8Rb/Lr/kkPxDw+s+ncKLlNCxtdl
2aj3pxScrhwEdnd9eXF6yCZ4qMbIhVx+z76L2phSMpUi+XH+jMzR7syfVZsr
pziH8z+aD2oFLkLyv3y+tr4XE3Vqjc3piZgCGLjDEwHJXJ4teiUObpXhswXF
qjWGo6ZdwpnQSDvhEdq5YWSaSuSqQhrQadoACR8OC/FZlrwj87s8PZrUgV44
tbSS//JL1dcpIr1mwBsSnhHyNmgyTJLsphObWbB4QGKkQeuV/JaWjbo9nv29
YadaoA5OJByKxBNZxSjV26tKPyVsytfMBClLLZDS5aT/YGdz7SXNXoQFlWUL
ii/41ls25eoUoskNO2aKxsABkvKS1h3qJUQ5CnVIzSarbDBYpmoA6bKiKNQa
gft1oFAYLcLPCiGAUZ0dTVtaLstpJbJ/p6R0u6qnvHKoFZDEDZslpgWfbDav
SHKpMz0+vwQwZ5ECsJwKYzNAjBbJL8a8Xo/L1W3YEk2sxkPBcCzOkaU2qMI5
ozI3c8ALsn1q+QKb1XQx7t3bpoL39p4vklEs1hpkCmAEkIFcuNoFYHxDpREp
LpPN81xWVcxmDVmu4eAQhH9gEUJkrEckyxq1iBTn/RZHJ8eXdMAQ7/6W3u14
1jVA5RH/Ec3Z4tUXLLmqnbJfCixHLX4aMoD8lR64ElIli5NES64J69GySq1k
qULM5/N5PK2ylg5F41QcSqbiKYEVsNs9Z+Tt5PTslHqdzszDZNC082mYv3tj
bXN71x1NpHI6TUdOFk6GuXSwHTwGjgakIKVTqXQSPiCk0hm11m7SGCkb/6O1
kV63Xa+Vi2YBKijoBRrDEkhCqppBmbfOvDCVha8vT2YIgByvQn4Wzy+YAlYq
INmBngGf4aHDVikv5gEWklKlvzi9dLgiBUjq8xxRdwyaL+oyF/X6/R5f1chG
IhAf0S9J+y5CvgAnBPYa08wcxD45AQI5Wi5m436rpGUTIa/Xv7e5tbvnDiUT
vPpn8eeEVECgjkXK6bBp8QlaIUoAWUJTBvVypoA8NP9JqziwRAB9VuGhORJJ
gP5jGZ2atTDwm5X8ZNjI6QCT6VhGI/kXzNsuWT35M0BhOof4izG4EpczhFQ8
ki0PqFJ4z6jiWwaMT5HtcPzVkqmJ6bDH5/UF7TyclPYBQ6FoNBaLp/i8ZlHH
ZvAZfS1nwKA09tesFKRMLBj0sgEK154nFEpJFC8I4c6prXPCEC6NSE3H7Yqa
jgm5RCLJpRJQVIkcm8LqObEqwpOH89Gg12k3qmX4AWB5MhIOBEHxxozirKqm
jvxny14pGST5BzSLdca4hMNOIDnSM6MotBzVLMrxmCxkktG01ZufQH6GkpCS
yPxBMJD9aE8xmwx4A15/UBMSCZrOEmhlARkwkRQkFcCBDewSZJ0SQgVE7dTL
Os4oHAz5XDRz5T1w+wNxXqHpn26fGsyzxeGSwVXYyqxTt7LJOCdF4jRamVHM
em+0SpQ3Tq+SpjuA+gddaKBULMh81OcPuJIGIPUhS1q3q5rBLU1/9ewEyd9i
s1inDjO9ZDq4ZN3ocyJo0xGiuZiJJpI0fKe2JkfgygRLaFUEVgSsR1uqtqHk
MvGAP+j3BMRUMp6Mx3k+BgfI0J5bghcVHT5A9IuN6jrDuvAZSUhFwxGv1wXj
hxd4g4FQSlBAsZqdbn92MkHihsbG4+Fw1umURD4ZS3GilBVjScms0Mi+swjh
lMNY3+EUz0wBmWbr+Yjb7dsLSEAgtDLhBFMW2q4pmVqxQBr+P5hMD2kY0xnE
uHCmMVh4Brof9Rq2kqEVJCSeFE+btJeMK795eLi7OcePTXu1sqUr+WwyEgoG
A0FfXhD4BOw+HA5HI0kaao2lMmyspFyjhVvWn26wOJUX0oloPEzM0eUPhCKx
GIJGRiZrofnH+cVyspwMx8N+f9wct8UMcn8mVyvK2ThNtQ7mtAdyRxiJ0Opb
htauCZFRv7pqk/z7nn1vTMX3AoBShHPyyQ2yybyrh/zAf9TJXxw606ircaTV
QBYtLvVbZT0bCcZD0VQ8EU+r9SGtElMcQXaEEZ2czkct25ZNUxNSsUwm5Y3m
ZClHWx5JZ9krxSVTiUySE2VVp0IQwXS2/KEqOYFDqICiAkG/PxiKRFOpBJfO
K1lZM4pI6uUBUsa00zvuDRuDniZLVFAocAkukcZz9yeHp3QWTpGErQC9YQUf
eO100K3bqhA52PUgsGT0KmzlkPAfwTzW1T+etvNeTyJPw9jTFZumkT7qHZ/Q
aPaSxjv67aopp/zBbBYul0yLOa02mB2dXt3R5hjbM5pPev1m2yhRc1gvF2sq
FcZoWwNOQLMXisil4+FYOIqAkKNJJTbFoSpUGSIGCi3RMiCyRSSWpOSua0D4
Mo2O6XZ1NJyP6ydHw3a3ZpYLOSEdl0TKf6LO6hY4iVev377/8KVURbt/lCrn
sNuiKkQP9t27e7uerFkn3H52wbIcka8TUDpubz/K8PZoxuIyU8ExjfUul06B
st+u2Rof8YRiGQ5Pl+BEkdUgL6/IR1h07Aw7jWa5mic757OVer+bz/OpNGX/
aCoZS2ZyHC2wRXz+EAURXqDpcKqhZ2gdghYU0jQmHYvHaGkoI/CKKCiKbMIA
qvXGYNHvdsC+WxXbNPNZISWbiWQ8lpLtJiU11rXC4X9cVXtJAUDsOJcx7X/x
scDBwe7uwV4wz2jO8WdEcXF2OG0boe3tUFavNFliYnMEyyWF2+XcqSLQagJo
TdK36/YDyUZCsbRYadqd0fx0CY+h2g2YXxWhtmybmQwZMqc2OrLGZzIxAOB4
SknFM+lMOp2EifsCwWAkmU7TBgtN8rG9NzGbodXWVJbnMzTeSwsiojPVZVbB
5rv4Da3ZoFqtWbquCGKqUkhw8RhfqHScsvWrt+8+fK5XO5vfr6jkSVvZJRX+
z6byva6IRApgJTh6UX26KOxubnkztNruLJKsqii0Es5KKLSbUjLkTPBgy+MP
Vdu2mIipnXKlPcQ3DfojZ023YlYbdsk2ZD5Oi1pxrZGXsxyXgWNnkryEQMCl
E/F4NOCHkSOJcLQDoMi0EsDTKH+GTVSsbIFWADU1L2RpclrU7VK1N2sjn9dr
rWbFMLQc3+aTiUg8R/a8dFrWsH6n4/Np1e68uyGsSGupfNjt2tnd2XO7PHHB
bNK8FYtz4CzDqhzY2t7YB+FmmzSjyQSJeT6noabJlGQDjqgTq4+5dj0utydV
rDeMQrvS7vV6oNPdOqyzXq3ahqaUizR0lUNuysQEu4f4haOlLd9MXsI/JBDT
Y7GwPwokhBOWaatXFHgImc5Sbdy2DR1C5yC0wAkSL8mQHhRP1/XabDHq96qA
V7ZZNRWZl1rhRCickqlqcXx+jeBHBaJP/7nbRw5wejQDatWziXTA7w25D7zR
SDStV1t9RAGY+Hw6aBTi6y/XN3ciok5wq78aIZpMqDgK6eF2zVrZVMWEf3fX
e+AHrkkU7Pqk3usCuBDCQNKza82KXSnpumkUCqqA+Mjlyn1JynLZZCIVCUdz
UgZAkPY3kRujtN7Fs/0+50KLnGZX6ywdNsDiYEIQW1Fz8A1BF3jdrvd79XKz
02pVa0WkDA0Iq2xHIoFgRim1Rqxr8foNM/9Vu4/JzzoeJH9ZF6VCLARI4Xb5
g56diGRVmzRMRgW7QnLzMS2z4L1MajX3+vjvYzZrSHNTPZCpGrXI0+G9rU2X
NxDwhOP5gtEbAJqCc7QJ8tXbzWqtZhWLOD/NEGmVm+Snhd50PEGpnE9Ew6Ew
FBANh2NpQ6I5PBHnnqZdP9oqBhyCtqFuGDmVUDRTzJu5DK8XBE6xzWJ1NBv0
Ft1ut9YCWOJSPQ7vGOa1Sne8JCT++u07Jj5bhP79Ezt/qhQc0a0UWrakpxKh
YMiztwdf33XFRTARsANEkuDLx0+evVjfOIjlCsVqo93t9YlI0bx1v8emXisk
firiXltff7HrdsdKgx4xrfFwNBhDO+VyuUU2QIevG5pp0gIXnxaLPVHgaOMM
/D9KGCgQCEdDQUDBNGJbLi/RhQ4CrF2ltRw2ksriDaJNs1KykeKA7zi9Jebz
ktFojbowjapd02gvJiVXEwTFBGS/6eHK/dke+B/O+j+16x8YKyPWpuX1shwP
+t3IATtbm/s7Lo83mKSFyMDWk0ePnz57vvl8PcjJRqlWb3U63V633+9CeNrM
pEUyQNqIe2Nz9+X61kGwMOp28bQUInptWjSjMc6CioyuVouGYcNqpWwmI9od
ODJd9BGHzYeD/kAwFAIuDEZiCYBACCVk+CzPCYUqcAfBDnAbwhoTxiMstaDQ
RHuxL+QsYCWrUKdmnWVXAZaETEkCmI4B/FW7E0f+d9StxfGzKwCcAPjqli4/
GLTKilUsiOlI0LUPDQQOQDC3NzZ29/a21l88fvL02bPHz589ebIfE1SzxPZR
qZLcoTJCo1opAtLiZ72bz19urK1TW7LcwO88OV1SS6XfgbXSQKpm6AXkJi6n
5HJCVstxWbOdB6xDXE+AfIV9fh8oCF6QP0OmT0bCCxmuQIBktQFxytYfQF5p
b9U28opRk4u6VjblQt4CbRxSOb9dVPkkD94XjzvoZ2X/TP7fnRsQGAKgqtT5
Mfk/UCToZTIacHldW77g1vbe3s7eAdvyWF9be/r02dMnj3596U2KtI5cpYFv
p1xO28+6ls+mIp6t58+f7e+uhSXiUPPF2QUDiHQ/C+0rUaVNKjdKugDwR/JL
HFdoqHlRkmHn2TQNl/rAid1IQKEEsDDAMK33CmmNVZFXzcBztgO0ZAoogUjL
qlWu9GslOFd9OJkfnRARo4Ced5bhEwAtbZb+/2v8Y+K/o/FjJn9RppINAobf
t7+9ue1a39ja2dlybb3Y2tqCGh4/X3/86Neff9kKpkSkoSKboqUefbloG6rM
9p1dG/jmpMvF08YP4UdnxJB6dzT63yhqstWpUU84K0mimIeEckVRTZta5WqO
TwUCPq/P4zrYOwCEQCAQkhJZf77CmjysI/J5cRlZieA2cJ5pAax0qKbfnR6x
ytSq/FPT+RSVVTit3HI2el69QQD47aOT/j5Rn8gBQLD/ppXP0rhiPOhz70EB
7q21lzDmne2NF2vP1vZol/npo19+/vHJXihJq5Q0p1QFNynS7jMeHWrzBLbX
fPGoK0ToaU5dMqc6RO0rYKglTb9325JIszS5PJ9RqUxmmmUGDUqGmk0ngm43
xHd5/F4AwDCAmw2mKFWG1HS9BBlhrZCrlQJonNoGcder1XK7UelM2NIOq1nd
3lwcL4ZNEx4QDRNro5oWdW3pHgg28uLgP2qVI/5DWXUTFslnUlGfx00rPXub
mxsvnjzfhQLg1F7X9rOnz2D/P/300h0BEGGzoUXav9EUBLJ40OsLB0PedX82
4g7L5Q5bILq5u/+zgsRq38NOCcdPKysFVUQe0ESFNndo8Lik59PRsM99sLcD
FurzeL0BTrWbpqhXiIycUxmZmrbUDGGtEMa2y9VSuWYa1W7bGUqkYstqCPHs
cNjUU+loMAbWggc6Ob9mQ3sfVhMPfxKA0+WkW9VzPNvDD7EBDc/uxubmsycv
d7fxOG5POLC9/+Tx00c///TDzxueSIrPKRohLrp/QsgkIl6X14/MGd7x8mFf
RCp1xsvVWawmb5gKLthtUTVbNSxbNzWJFpSy7AobIgaWnMHv3ofudzwHwajX
G5eKJT2Xr3bhvMTc7+6pGnF7e826odRL7CMHltrlZrM9aA4PIR8DeB/eM1xz
fb4YNsRYLBKmthVtNF1c39+vxlZW7WqmKFrAaZdUyJHOpmORUMB34NpF2F9b
39rY9uGJ3JDM53ny4tmTX3784dtfNtwhdhMTLd5m4WJhv9vjJszj8blDqWA0
xpnNIQ2efJb/9esH1hy5pfbAlC6LUYy6JQPdpDl+MgOWnoA6WnIqEnBtb61v
b4KEh5MRVS3YqlruDIBdWcd5NWPOFMAubug3q9VOq1yykGzmZ9cOvmGDWHSn
1fXpYlhORKLRpAgDGDrlj1cPb5x7QFibjAZeAf+m/YZJ2SgnJJMATAGXy7UL
GuSLxKLu/f2DA18gEvEdvKQA+CMsYG3PF0mkabk0GY8EPAdIEwcuvxd/uvfD
wUgomi912IA0NT4+N0g+a+D0cNwpq1LdUmk7iROIPVJPrGZIiTjS7vr62sbe
1vYBp4g5RIpSp79gTQRncgdvwvoM52fHFFDGQ2IddrXThvHfv/4c3Sm2IbJf
ncw6KuHpZN6qdcerMZnV3Ou7t++cy2/OT2gFzzYkDkQ0lUpEgh6Xz7vrCwRC
kaR/JxhAQvCEd7e2f1l7+vjX73/87rufn27uexlQ8bv3trY2NvcOdqEAn9vl
dm27AsmsVqh02QadYwGvP/fHnBbR6XzY0JEBgW+ymkwkmpYZqzofDuzvIOyu
vdwACE9KAi0q1vujI2o3s9YWe5NXZAAXZwgA01G/VqmUQP07w+Or29dv/wQ3
nz5CAbcXR6MqT5dh0FqzMyhCgwKsH7Ead6bZ22m/jhQuU5cgFQv5/TBkP448
HI57tjZ9/nA85Pf6Ir71zY0nP//w4/d4/fx0bXMb6XHtOUDx9i7tQm+5A3v7
8N5oVtKsslHtsxoiU8CXMRt2frdsOs7C6YP5yrnDYyddl5VkyLu3tcMMwO3x
cBlA7bIK+nxyuZq0d56auoxXl5RTp8NmpYIsZNd681MkN5w+xF/d7fXx/Zv7
67NFW0tEoQGO7XWzOblV5/Lhgd0A44D/EoFyujciSdQ7FI0AjkfC3h0gWV8g
GkY28nv2Np8+/v77H76jP7777sdffn30448/P365vr69tb0Ni/WD+R7sRTOS
IptAhPXB7PD0/6MA9qLe5Mm8Vy5oSl42K6dnq71YIeylxQgAro3tve0o2KtY
MWrD0THF7Vd/3l0DIyIHOHW0VqHJou746ALWD+OH+M79Xshv71/fXR0PKulg
BN7K502nVcy60dS7o77O9QVN33TKhkY9cro3LhoOuONgoLG4a8fn3TnYBwJG
WN45CCATPv7lpx+++ebrb/723fc//PrTD99//9MvzwB4N7Y3XC7Eiz2EAOp8
aXaxVrGapADWl3/1uUvsCICYe3W2GJQM2yqWi2eQn10KmI0n4z6fZ29rbW1j
1wU8mc7IxqK/OP0ybfXu7apue+Pc2wPUXqk26uXyeH56/ZqueWPXnP2D3W0I
D3jz6vpk1JDCESpHJVmrbDRbsM42W/q4pB2y+ahTLxV0OSvL6WQyFwknYkIo
QhvzO+ub2+D8G9suP9JheOf5859+/PnXH/727Xfffv/9jz//9P1Pj5789Ovj
Z89fbO97Q+EIyKsnRAOsBtBR1TAb/dVgojNy+MbpzbPu/N316bxbZMMHNHY1
7TUtWclrWdD/aMhDm7XBSELI5Gu9IR3/n4MNzpweHIBGKRC2K/VWvVyfHV3c
0fH/Tnec0f1+7GbL3949XJ/P2lo4BBAcjiYF1aq2WPn6eLVJTBvpdH2jqWq0
gy4mknwmEk7Gw25fJJlALtrZ3tqAP77c3t7wb/3w6GcI/wN74eh//PHH73/5
9rtffnm8FUzwOVlR8mImWWA7R6ZdLilQgDMsd0vmu5KfTYq8fbi7Opk2S2Cw
Jci/GLVsnIBqyiLYXCaO/BNNGbIulBqduXN9lyP+Sn7a0mDy091D8P/O/JSC
/2+f4Pv/5rz+AQP47T0i4LJvxEKxTCqGKMjlCrZTv5wvDqlPhAzaqVkFRWa3
6UgcyGIyHEzA970HSOkHhAEh+/Pna892D3w//PTjk1+R/3784bvvv4cHfItg
8Lcffnq8xzghXb5RNDVdp4UBE6ZdYCzIQW73ThJwVg5IBhrPGACyF00G1atg
UErBBAsoIA8ngp5wBv5qGqU+GzanyTaWsz+8f/d5xYTWPztVdj9hf3mB6Pf+
t9//zm75c+75gwG8f31/eTQopkJxjl0dmkzxMjVX6erEIStItlt4TDlPl0dl
aDc6nQiHge7iyZDPk4ABbK+/3Ngg3vt4+4X38feQH6+ff/zxb99+/823333z
7d/+9s0vB0k8aqvbHwz63VbVYksMdC2dqeQKTtK5dMal3vx5im8QAo7JACzj
/GQ5bJZsWv21aSbBUCUuHgpFEhmzaDaBIx1Qy+bVabKJbVnds6r1qFW28DON
wfLy9uHdh0+O/KuLDkn+N68uj4YVLijlOS6f57l0SsjSTTElWjMBYzJqNb1Y
0YiP83xakLJZLhaJx8O8FPa4wuGD/f29vT2a1X/++Nnj3Z0fHz3+5ddfgYJ/
/OGbb7/95oevv/7m6+932RAau7eUKFmrxKQgJygoglZpD50gcHvvNJ4cBbxh
F8d1QSBKpzQuBZXBZRDLq2VYQo4DvEQSqZv1CaAfIMtbR35nxpBdWUhFm0Gt
ZOqlUmt8dHn3+v1vf8r/j9X5vyX5q9m4lBP4nCiq6TRgh6LoetGmrorIW+Vq
pSJwMg/ol0nTDRGxeCoRCIVpzZFuM6BN/gOo4MXm2ovtp7CDJ49++eXXX77/
6zfffPU1vnz9MiJZjf50eUiNZ6K53YpBDmDqqqaIAkPeSwJeDHq+ZSPHdISU
m3u01XU8H9RLdHtNg5U2qyXLUJyLQNr1Ymu0PLui8Ief+gzaoQAm/+GkQxvS
pVJ3dnYD+Vlh64/PGqAA+OHtqyvILybi4Ox5WQbeAPEGb1FBttMZ0ZSTuXyW
y2RFVc5xKS6dEdKpeCaWycRiVDmJUYMxHASsPdg+2HrybPvR48cvnv78688/
ffPVX77+61df/fWvP3sEs+6sGdGgDvLJFAqwaUxfK6iyqBh6revgjhvK4s7i
DQ2ag570YIclkBTatao02p0u/LGBIFIQNYNXEdyb7SHs/+7152UDxwOcUQJE
zUbRNsul2nBxcfvgYL8v4q/kv4P85WwmxRFbyWUSdG0VqKuSh4lxnMbxipIT
U0lNSdJ1aewWqqxMW8ur3d1MOpmgYjTo6M7Gk92NR4+fQvofvv3qr3/5y1//
+vVfv96Iq9UezUvQKugdaDfQZLdkwp1pqVrJK7qglpqUB84unKHRFYjB+ZP9
25VRqwoi7ayoIoLQaIyez5U6hzWrUWbLNncPq2WT39iUPi0Zwv+Ppr2KXW8U
S60JzP/h3W9f5Gdf/s4Q4N3lYc8WhRRd45XNJDN8lm7/UaWsmM/QvGGKboji
krl0LMVn6bbZDJelmzVzzou6TlyGOo5Bn2tv46Xv6dOnv/70/ffffvX1V//j
X//y9Vc/e7N2m2prZN2EKJldtm0TXqwbdI+Zokl5vdxmE71UEIETEBKmA5y3
aE+xgyRosI1GVrnr1CslQ83Jumm1a+Vad3aC2Ebyv3cm7VnflkYpDkc0ztmp
l7szZL8376it86f8q/x/CyVbdAtIRuQQUcrVIi3PSBKf0bMw9Wg4lZGEXJbd
rM1ls3RhoEzXQ7CbA1R2S0xOZKs7Yb9nf811AA8AAvrmr//63//7//j6q6/W
41qtP1v1+D9Du8NRE+GM7o2U6GpXs5AvmPUuW1KhXTxnqIp2/puUKJDlDMrK
wyG7/LFHrYICYodZbZar1TaQ7Q2VrSj+fa5ZvKZrGIGgy/VKrV7pEfN98/7P
8/8HYwBI/3B/MEAjw/N0j1ep1RsO+62iqigiB6qfShAzSCfzKswiw/EJEadV
KCB6ORdj0cIhtZoUSRS4NGihd3/T/+zXJ09//u7bv/zlL//6l6+++sEtWO3x
4dn1nTNU8O7Nm4fbq9PFoKxbJo2VKfSWBgKOZkMDM/KC1Uzl+cl8AMMHUlBV
E6dPsy50n2CfOhsGTsCia13san92en3/8PbLpiXbsKPpvnGjbNGGc7W/IObP
+lpO/GNX3AL+viXzHzVkji6Y44u9KV2tPO5YophNZzmV9weyejbE04XpfDKT
pev3qKxH14iVypVSmQZjoQq2uAEbiAU9u1vrzx49+vWXn7/96qu//Os3f3sW
Vap0WTrrLLAXhaaLo0nLKLDroNV8XlUQB3S9YBRrHecWl7MzKt8sRm0CCkVD
1e3PF1/TCEWvXa9YiB10X0HBLDZHh4huq82G3z6w/Rp2Y0anPmnJht1sDBZf
qD8jf3ixCgBAxjWOopIT4Pu8jUhKV3ovBvV8PJWGQmD9giKmhEQmKSAy5BQd
wtO+IV71eqNeq9ZqgJdltsckiXwqFvDsrL/85aenj378+m9/+de//vDjbsbA
89Hxv2Wj92zzgjLboFIwCipd5Ef3byAKmrquFOwyjaqxOwhnwN3Vol0sAfja
5aZz4xrd6uNMB9P1NbABRTPKndkJi4DvP09t0HrdyWJY1euDhqxalf6CrjhG
/F9V9hn5+0StHbYEZNJFqbwxOmI3eoF6NwvRGIcEF46lchIyXSyFOC+pyKR0
i1aXheEetTZa7TZN3lSpnVqQc0I6RuWZp8+e/fTd377+21fffPtrIFdk26DO
WAHlp/fv2eT5pAk8p5nNmoEIoEh0Ua2G8wT0AmHp0jZbu044iSaPYRjtvkNK
qKg1HSIHmBCsSPOoqlEbLM9Y59ZJnOyueuS+pq4aer2p5ks9eoIH1tn6xG43
Zq1dOD9C7GxQk4Vcjs/3jy9pmuvm8hQBIR5PAOeDsHFiNJzUdZ43bRqiarEY
PKbbIJyrlLrdLtRAzT1LV/NCKuLdhfwvEQC/pj/X40p1QAH61ZvP+Zk6SmQA
/RLNEzeaJaDrAgiGohUMupEENk03BRVtCywRf1oIOGA5zlAhzVEd0zBOA8HH
hg7oVtFie0RXz7KlVcb+nQU9Q8ppilKQ5WKHAtAruuP64+fK/kdmh1d0qXUx
jydQm0dXUCGLzvOOnklFkoA20XgsGkykbD6rFsvVVpuuiJjM6KLJxXT2+U6M
fr9LzdayTVuHieD+5suXW7/+7W/ffvPtNz+5yPwZQHvzn/Lz29d3l0fjulYo
gG2ZsiJppiYpMl2jS9c70R2xMAW6VhnaMAuGzWj5krVLLp0pmVbJNGkYV85J
glJuT9jGHSt/0cTSGYlFd9cIWVHMFdiW4+2qsk+zHXQKzA0PJ72qKoORDY8v
79lt3SR/SyNUEwv5A/F4MBDMyFkNnMiZ6lgs2d0YNM+EYEyNVna9eqdJl+op
uVTYvbO1/fzRj9+D/nz/LEyF7qMvcwW/OTvwiDs3p7N+q1VpIILqFsC9Jst5
DYBAJocus54N5C9QA0ArlpH8KDmSf16xisSwW3ZyBxWYRa3irJyyIbJbtp/Y
tBQpi7SNwCbky9TcvL5jva0Pq8Gmd6/vbs6Ppv2aTve5D46RIN9RcEbenDQk
INtkLBHzhyKhUDSZ1Wy6xmc8pzt8nJtF2CVzR2ymCzoAKqEL3q1Cnot6d7Y2
njz6+eeff3r0y25Kq7JHu3/9RX6WoB5uL05PZ7Sxym5j6Q2qdPmDhsNGHqS1
A7qZxaT7iRAU7CLII+Q/v6BxWuoRsN15oHWJbgLFn3p9SHPU9H8vL89ovcKg
22Z5GiDgUhm93mf6AQNmq0jvP68gzwYNU7eLxf7xFf6fsxV3eTQqp6MZWD6X
CUdC/nAqVyiygXt2wdw5G+m8cMbt2VAf7dzR2iWCsqlkE35qBz/55edffv3x
cTBrNVZ3ASA6rdZpCaC9vrtG5pmNas0KIn6n3y0XCg6aUBRwI8NGCMD5Izkq
imJaJSoTUH/rxllBpHqAgrPPshtQs0IOv4aWDs7PaQZ+1q8bNA+DjMwDriei
OeRIZ7bNKTCwi72vAS/hJSZibPvomooD5BSvbqggmkzSGJmSo7G7jPNZEpO5
c5kNm2heTZBf0GAj9ZppaatPDRpNTAb21p48e/Ho1193t7YTaqUzYmNFDyv5
HQMgBzhbTJBCKyaQVLlmqQZgBP5CuCrQhj/dv6SbiF+yqhjFiiP/1TWboafl
7W45L9InkYjsApmUXKrRivfSIdhlTea41WB7LJ4Ix2VaSmOD9q+cIjvdQQPx
O2W627O+vGTo8COt9l8eDssCJ+SVnCCZdGWwpNMCBQ7fKQwzbMrm2R0VOEtX
9OkywKVFLZcK7Dx98vTpo8fPXS4vb4D4wv3v7j9vHjIDoOBze77sVRuNRgU4
stqwClaZ7h9qNIjcIOEVi7R4AVxEUBvn38EBsk118m9iUAhvebrPOiskiZEV
rGqbRvcRiMoF2iSmIcEkl0xEAWJCdL80a5E5HOyWzeHPhp2yZZdq1cnFHROf
2PDN6bSlpNPJNLs4VBWzWdXGL5857OxuVah+Teuw92zrjprN5ydLNrpXL9HF
t5vPXzx5+uT52outKGtzOkOVDJ58lp+1Xo7GTdphB5CslU12N92YbloadBo2
Yh4VOuyyijCgKrTxM6LxrFt2BQ37JJKiSdf35fNZPp0SFUnSDbq5iiKpmM2B
x9GIMXBbPBKji3eTGgjW/MjZSri8oLLmdNACBq+2Gv3T29dM/N/ABi+WYENc
Op2WJYFuRJMgfvsLO3fW56i+QC5EbQZn+emM1g6BSsqGlPKtP3/+9Onzly83
XJxRH9AtgavN0/8kPxzt+nRMwyGdWmW+sAB8V6N07ArEuqnZFagFxlEESlbM
SrPHmrfU3mT7Yw0TDFChy/syaUWn6+2BhhXNrAKKqwqYG5eiTYF4IhBKxCIB
f0ort/pIocfsllG2Yle3FTrbzvL64Z1DHMCGjkdwLIGKK9k8sIWUN6vUFKHD
p03W946iPlKRjTVa7m/v2BX5tLU2aFUNKel9+fz5CyjgxWZIKhHzvbi6Xe3d
fZEfBvBwc3GxGPR6rcbsYlLvj5fHp2yS9MqxzHqZFgTpjh6jCD8o0azMKdsS
u72+OAJoU9gF0EI+J2dtPZ/XC3Q1XoF26RH3Rfp4l3g8FIxFgnCAWCgQiOfJ
jWkmcTal699oOCwH126Oz+8ZMGDPdDptqHkZkTUvSQoyq6JX2PY4sXc2GfIR
2OmTMxlIYfQ1a1tTTjpeMPlzCdfzp08eP3365MV+qlCn+zUuSXX/RX7mAHeX
dxcDoIfu0WF/tpidsD7Iqgm+nIyHCKelUq3WqlToUqMatecvadGXtkcnXZsy
H8xf5PicKspWUaMbO5UsdczIfDnqE0STNAcMZh6OJ0IRXi3SFgDVkJpg+fhR
WiVsH904xw/xb8/nHZPYf14S8wp9cEKh5IwFO5+P8fEjYw+se/bxtz81QD0y
mpBtV/RsbH/t8aNffob/B0QAU7oKwHGc/yo/Ii1C5xhHMZrPp0sKkmQlhN8I
wBwfOx8tBPrebNLlNrUuZXi2S3JxDGyviaKUy8uSlFMEQZDkHLvGMcfTJzRk
0qkMn0lEUyK8gj7vIhzLkA1EOMWwYVMlhlSTfDprVOuj8ztixg4mWfZteBH7
mIycosmSTMvTc/pcD9AX1jl1Wgf/YP1TUsDbVbfxHDlp2CoX+ND206cvdp89
er6TUEHN4bS0T+FcBcD4+UdnshoB4OTiZL4Yz8a0kgGKwK6LWvVu2DgMdV4a
jVaXLvlrtPrUnL66ZoM7XZAG9gEYMFE5k83ls0ADdM1zLsuJIonPZ+KJXMEC
M9Wy8XA8GgiGgwiFSZ4+HiObgTZCsZQIWLe8esWIE5Dv5eGoauhgJTmaKSV9
FioU+wBf35D4f//jH/+2+oAk9tFYf34+zB17qn7DVtPeF49frm8+f/LMw5st
8n62CO9cp/HlOhGaPoCzHV2dzifT8XgymsLEbl9RDRvkHe93zzZK2CpYb0Al
6FqjR1dO0z0P1IxWeWfyU6SxqhSYN92JrWQVW8um83SHL5eMZrRSHey0Ykow
/kiQBicjQZ/fHwj5PQdejyeUEgql/sk1fUrLW7YNjqxiGQWD9igoBOTZ1RmU
vmkqksT/5z///T/YR4SRBv7+yak1rtYWQSXqlhTfW1tb34AJrIfpg1WOzsj5
Hz5/tMrn21TI217fnM+PDufzw9l4Omf8hdXwmUKpDQ4mRl416g3LdEFCi4YF
CeAd0iSWSDeG0MX9IiSNRSMJLkvDEvTBFxlOpFv9UxHBAmWhemlRSYQjWTHj
88EKfC7PPn2omscdiWXypfEJcRPijBdH03a1agEPybJRsfRKRS3QaPopVRc/
QHz2AWn/D17/AR38kxTw+6cvE0JwynG3qgv/L1vvwSW3dWUL/+U3Y489tiSS
HSvniBwKQAGFQuWcOid2M4oKlGQ5zPv+x3f2uagmPeuVLK0li2zWTSfus3fy
rwfH3/3xD//xh++KJoe+7Pvfi+LEFx6pH3/4SL72bHdxdn69XNyczfbQHE7g
OUZ9h4dAqcx8HPa7Ya8/nG3OOLqd9hyyTE0VUPCaVMpQtFKulsrNIrNzSo1m
PpPNl4o5yethDoEeUVsr5Mk+5I8OX6YOXxz891++e3lweJBNJGvB4uLukUdv
bu6W3TaFHJ1dv+FOZrMJBZF8/HQwFB1BH+5vWP0/6fOPf/xOG8DqcHwDRL1l
1nPV0tF3f3nx1//zn//xH8cNd0B35+7x7Z5L68vxIwNFqHl2Rut/3K52i9lK
GBkuYHCKAtuCYvH5ZjoABUEPFYDtdr0ADpfMU11qAPZcyRZqYGvWUIArVxtV
8gvFVL5cqZakNkTaAIMc+GqhUG+eHp6mTg8OXtL6X7w6IoNwWuwsAEIiB3Z5
8f5htaQkdno19wbkJlahYgIUiOLyh0/i9P/+z3/+iz90B8QT+PnHH2NxvIv1
uGM3swff/jnx33/4z//zx6waTDYXYrZxT6TzoxisEOib9093F7vd+e5stSA3
sFiL2ZNnPxGrzqEIHHbAM4XCGGWaKM/KAKJJjVKpWCpLBigYPRfwFOQCFPvm
MvkS1ByAsAG6dDMftGXK50+OT3LpJOhZj2kb0icHR5VgShbqhnKBzezi4XE6
GHvz3SKKosF8SnlRgObSwxs+/t9+//s//vmv//mf//m///M///onvYHfuYWM
HgIlzQCsDNp6JZU5flH463d//s/vKlYP8n+iM/Updn1i9Vx++kQG8AJKbvMZ
5gOms3XcIngeP+LZk4frzTLwg8CPuuBcGPYBEdXqRW5WFnI1FCbCiMtwvmvI
TVAoFcjO52pNIxiQ64bJ2NJ3kwRuo5g6SBy+eHH88huQi5S9IUb1dqvZYLg8
u5j2R9FsNQq7g3Ho+wDNLM9v4uOn5f/jn1g+1o8LIGwAr4RimcvdLHLkXDF7
cHz63Td//K+TRntId1o0pj9x2eGr5f8sWg+Xa4rFeMwYpKtrZg15/fTuywWg
i3W1XYZguoow6QdrrhomKLshp5KrmV6H0h4Q+s4Y7a1IYFOFo6tUDae32KFk
RL5pMXCb+UI6mTkBevK7Vy9evDh59fKbnAXi+Plyu5mQfaGYuN8djbsd9BgD
Ss7A43f3+O7jj3z8dPdp9fSh9f/z+QbAlL2DyNMoMGoABr86/MMf/uPPWa3D
jak3nPc+Oz4sXaCvAD24XlOcR1d6CKj8gEWYKNCmP5BJg0AU9Pr2bLkKIzA1
dnyv7bUMVdL1hqw1qpBDELJJ4Fbe7TZLjKip1VIhncumC2qrpdHtRsrHKg39
VrVQyKcOvvv225eHR9+9IjvwAmNc4WDUXbx/fbueDoYoawe+S2mU7wftoIPr
f//04dOPn38l24fbT6v///7vv7B+bIC4AMgab87mfU/JH706PXz5x//84x9e
lqwes8C9+xC3ZX5i2N3n/YexRzebOSXWlDj2+0O6xZQC0lFc3gkwCzex7i5X
43mH7mLYcW10DA2toVqWqkssO+V0uS7BpOcXZxQxRq5SzWTVRi6j2WrNGnHM
zBnzLDKrpUzy6MV3L18cHH373YsXL795dVqQDZdizOunm/P1dDgYgc+vDSq5
oEsp2fzy+pqeP8RB/4bX/6/99RdOgF4AogDO5TaT0K6fvjo6efniT3/6j/86
rtPLOhdl3y9n/5mjZ5TfPzP47GazoQswn+L5djrdAB3uMf02Zg4BiAtAwMm0
S+FPFID8HU2PetO0KNKHkqqJrOBc8ADd3V6ToRuFjpQptAJHV+mC1EY7RC+P
T6xNEWrlQiZxdHDw3ctvXh5CYeEwkak25VbUv71E/jKlWKHXJwvTdn06/OHs
7O7umqKyH36m6y+WH6+fH0C8fizk7nxJPqb46r++PT0++NMf//SXlOqPNyj7
xmBicfU/77sv3Hp+/3T98HS5BZkvLb/teWhxR93BfAcpsgemAlmi3A5BHmRB
Ak3cbGojS9eRpXlMsbxvLEOKYDYIrEpOC8NGPlMv5ybbDfz7Eyh3NmO/WSil
To5effvtNy9fvDo8enWSrtSbhm+M7+kU6P3MxtNhbzQJA9cjj0N57/nlzes3
0Ab+2+9fH3+8AXgAvwBDAyKZbqueO/zzX1+cHn/3pz99i+Bny3Db73/YOz0G
Hv7K//sFz+bjE33zy+ViDkUz8jYurl1AoR5aHZCCWc0ns8V4PGvzc2xxpxFS
blLYJzsgSzqI7da7G26av2UOCkzpqOVCupguF/LlpL9C9QUVq4fbi9XQqeRS
p2QBX7w8eHF8Al2eutLQbad3cTahq0gXYL4eDueTtgc6ycF0Rlnp49sv649X
/q+9AcD5//wDrv96RDHWUSZxfHR6/PK//3RYc/qLs2t0fWIwfXz2e+gBgucP
T3e72ajfG0aDXoA2pwcS8yCIMNM+G48nvQHlx5P5otP26W6ALggdU50SMxPg
cMXsjCh03l2/5ob5W0FqOOpYRvE0WZRq+VLBItt4CUw7/ceb80Vk5rPZ7NHx
8eHRIcC7uVxVlVpmK5jM52fnW2QbQzJEPa/luF47pJTj4pZRY78K8/+vffzz
z3/u1/+ZzN/jzW4e2bXEUSpDecbJYZLsqjdaC+sf442/Wr5QVv7ph49v7nZT
dE5Q9PPQ6UQpzA/CCF/DJ3c3gmLHaNIFCVHbFwSvDm2CqsiGiaYwQEVbWj8j
Jt6KxkfP9tRi+qQkV/P55ng2394+ouhJIdpu1pHyhWw6eXx8kkxkMulcoSpp
lkJ3dc2pxWYzG/SGXt91LcOlUHgCD/72ww8/fqbg7x/xsvfrZwfIx/9wtR5R
hJlMnGQTEK1Wilk9ELAMPH9h+X4Ry4/zZ2CPPr653YHJGQMyrgcGYw/3vxsO
5iGPtIcdUDwOR6Dqd902uGjASWNqqgkZYcUKERJurl7TK6MEltlTKAzzdFup
n6STiVy5EQ17nOFgA7jnxvD1xHGaUoRMJluqK/SSQrjJ1w8Pt1CViHrL683Z
tGXTn0/pO6AFlPtQ7E8X4J/x5f/X3vz/9stPn8iNnS16ZjVXrRbSiXwpnyXH
bEXi+SOU+TFefgw7+03oC3/+8eNbWn8PVHIwfY7QkyUP0B31/E67G7bJ6fX6
g8G4R3mJJ2ZJaKMso4XCeFPSzJBCH4gvvPv4KVbpvUMYbtQoNDxNJtPlktlR
ow1dkHdgVwDUwS7RujMJegY52oNKtaaYsad68/T6artb9MN+NFuvph2KOgeL
Hfu/H+nLI/zdL/5f/xRJIIU/P36PkvEwMOrFqlJPpnO5crVZajhCVJW9308/
fbX8vcKyWP/ZNIrCAGfveyBz8OnxjwYh34KO44eYZh3Mug5zdYc800oJume5
JnT1bDr/+XKD8i0a/x/5jLfTbktqJNKpVDJXLRuOZI7OkMECE3xzPo8UKKVm
ixQj57O5SjHfMDvT3RVfkTf3Z7vNqNeBMgBtudvpUXZwzwaQA4B/iOsvDp+X
//NP8OK7s4mraZSOlzK5VDqZNBqyPxKJk3j+nz/v7/7f9hLTiBuwflonzB5u
gBdCfWC22AzpIuAreI4XdWlDOmQZAia6oPCXDh8aU5quq3j/i+X25g0yhh8/
xT2tRd9VCpWa1tJ0Uw1903bmgAegXH1/vZ20q8VaqVxpgGs2T1tQtXsLbo5+
/IiMdDsddEBrDVGZoMvkHG8Q///C6R/vgFj+7zD+MGL3F3f327GrSE3A5AqH
p1W3oncmW/yhH7hm+PO/LV/Iq+Pm0PpnZG3bgQuYA7DnyzXoBxfTUZ++g9eh
qJ8MQB8oFjKHfVAvBo5hBQ44nk3F6KCge3b3hv+YH5Au4I6PPKMzjchOKlq+
YoIpZ3X5wAEVwsm+Va7VisVmHeqX2XSu5gzXF/xSgQe43k6Z7KZlg1kjGMzP
btAYpQiI899//PMf/MHqEfsjibneXF8uRh2XXmRVtWqnmYxUsWPMx/uv1i+W
/3ssMP8rzv+O7mPUAw+k64B+gqkEhezmfNz3/agH9eoeSOcCiksgjwH4rOPa
QpGEBTYuBbJBNFUeQUPUXSx7Ppl1o5RIVbW6pffJFT8hoAQmLGiWaxBzzNeq
xWwmv18/Sk+Yh6FoBLy0DmiUvS4zWQM5iBdAG/D3v4vqz9+wgp+R+dycTQe7
Rc9vaTWjUW5WatmTVBOljxveVHj/z/H6n5f/OzvO79/d0/p7zHvacnszsCZy
b5WFOzaLcccHM2YnwklEw9l8uQTDURTZpilZhtlSPVo/3P+HGPf0Hirtq/HF
2TyUcMdz6XS+USja0WRHdhyF6juAO1gzk+LISjNfzFXswfLijpvfgANdLUHB
wIzetAm+iGLeM3AeBaDfufr3O/DzIoW5Q9WsNxh4htastCy9VFOyBQp++eF8
vX4+fv7N+BEIHD+9e7iY06sOYda8wUIQ6vD4HjoqZ6tJ2KakKOw5ZAlx0pvt
ejEbhWFotyBQZUo2yHuRoH8veIXJgl3vFsOuNzZKp8ly8jiRohP22g13hjLW
IzjfdtO2rjR1XVGbdblcU5tqd85e/sPH9xTIXy4geOqwTKZtkwsEuv4NNvi5
+vu3uPKDHsbd+WrgDfqeT+aoWapqWrWsFcpox1/efol+/m39f/+7MB5i/VGv
x/OxLRDB8Qib4Ep7wMj1CBcg6jngu1tCH3EH9BfEDlpkAKWy1hEemtfP5ZL7
i82075qeXE+U8geH+UQyG5iFioQ6FwgWKUdYRralthyIm9UqjVbY8gCPe/MO
HoKCxNmAQjLEI45lUxxM1xIFULywnz8zch7Ra1zAQdo/jLqhpzcqNVWu1Bpy
Qymn6k4vRvxx8L9fv7j+f/97XD79+dN7rJ+edBvFqy5KoA/xBB9fVbgyCkK7
fdePRnPMdl+cYT60bVltv1GpV4sN3Bq+n6gYYlAdxx+2pHqWFn764qieKPrN
bLlc03pLFPoeHlhGo2MbdP5oGMhdTzIiICgfwW98d7kd9YdRP/Q8AByRBvJc
PFvyH+IE9rOo+r1nEmf6Yd2WDvC4Xq/ki1XKPfJye8jP/70A3Py/1k+R42de
f2e+mHTopmkOBdv8LWIefnDsU1JJ+dCoTa4B6Abo41GG57dN3WyUIIbJSgt3
Avz/kQJgzDN2Pb2SSZ+eUCCayDe8SqpUyBcb9mBF9ws8PZtRPzBMKJ/JiukP
GxXJFXfv4R7I3AmgLOwCKB+hxAsKEVesZSEiWUELg9Lk3TXw5bpsQYTOUC1N
boCmoN6wY7/5nmfp9+4/vv/x+v/2y+cf3r++mLEmXZe8uuJPN4KjG3/x+oFN
G/QHvS7X/lnSDIOIoS9rhlyuUqQpQ7udKZs4AQKgh66HVMhTGpJMJlN1M5vM
F0uFXKnpiP7J9fmG8gmmHZflutUf1UoVzGJuLwB9XE9ni/lsGEVdMsk2pQCw
vONlTAv18bkuKSbUtvOe76jkKBxdbpqGXCuzhqgWjGf0Ox7fiobpl/XzBvw9
fgC/8vqno9EgWgxt07YUj84SGuTgqHzip7qehEMwjw2XwC4weH5L9qklUQJU
odgtDUcroNVcw2fEO1iqTk6PTxLJjCSnKMgtgRGnLKPUeYFJqnHokf0gg6Xq
bt+r1QB7DkfoDM8m4ymfP0wg2T/XthzP58vHE3bv9wA7UCKdrcZkiTxbqVQb
jaqkG/U6GYCKpBo+0EaAW8WT5HH4+28XAOt/9/pyOhwE4SSkeMaxdVdM59+y
GMvD7fX5ahQNh4h7VlwS4d4frd+E/HEN4VuOjo7LJew14pH+ZuH0+OjkJJWt
17JgDCvXWDlUx/j7jpLc8YgCDtMg+6e1IldjrUOL9VHBZz2ajskChnT+pgkN
NAo3UWXBiM4emM0QrNW0B9Ep11PA+95UQVdQq5eLTcmAKYupNL4kf88BwJf1
f3h9Oev3O30KHkzD0sjcMofFxeUlaBxwG/uUA4VRBP5ikCmiy7qAxibg2lDN
ypCrGS0gYEO//gosRCh/pFPJ00SiKJfS4EeqYvHQzLb8PjoIk0EPxRQyAabh
BBrg3K0WIp4gAp3eeDoeCtZLz7Zbumm5DviGBaXl3R3QHpdnu+WSsrIwDBxN
tzRDrzcV1rGh+LfcbPWZSYKsvwCcPuf+Xy7A71+tv+t7tM2WrrY8+h6s37Vm
bWUy9WjHdY0gWm8vBDb3Yrue0v+pSFqVso1kMttg7ePNFsTX68WYzqSRSxyf
Jk4yFaVSKNLxV+VmVZJ1W7bJl6D53/F82wKqEoJJ0FKwoYrtuAHFmsMRk9UM
IG1ht6Cv2goMh9KyATLtszMhKzpHx2LYjwZDp8kVFNNUQEXSaDQrpaodwSa9
efvx+/9V+vkSAj2vfxp1IQJgYczHszoROr0hC9VMASeC2t1s7HfInl7fMs6G
IqDIoRxAr1RyiUQ2mWnaQTRiaUUGINHtT2I4OZHKQ9+9mC/U6J2bUMHUDc91
MT6lu8GorbXozyQzQMfv+pirwk8Ba9cKEuqTXhRC+U83Ag8IuXanN1isdqv5
ZjWdLta0AysyXb2OLUum67mmKTebtTK5/2a94fVXD+SLyPo9Lz+ufny1Afv1
U9Lf6bWj1TjsDcn8DMgSyLJm2uBe1iTT1mRzbPKoOHMobhfzfse21bZbLWaO
sulUtlDT6eYy0Uy3bQF/ePTq+PDgJJWhv9K5fEnSVTdwyZwpMjAiUNBptRdD
vGxH0SzoRdHqJvzwmPWevey412mDIg7Kki2wQAfB5Gx9vl5tl7MVXbXZcrZb
UniqGe3Q0CVFrtcxHkgZoNxeIGAUcOvnkv8vX1LA30X8K9ZPWX2n21kuYHR6
s1WE3ntNkiWFIhRQaNDP1mUHAN5LPHBy//2w3XLafrN4mgYjFGVxkm5Dgcpp
ac1S4ujlq1eQlk1mMknwJVd106Z43rWNlq5qNh5+yzbbPVPRbaCLPbcTCSoW
oXn2GIM5RiFdSMPA74UMJDCo5CWvwGi33uwoUZ1frLreyncHdrWhSVKlWi3K
9AZULSDj9+7juy88Qv+PDfgbV87o/ZN9Dzs9erlogNDTVJQ6zEhD1nTV6rQt
Q1NrDZZHPoMCwWLcbZOZgEa9V8knMnkUsvJFDOXIzXold4rG/qvDVwdHqXSS
jr9pwLh1g8D3yZ3T4TOs0mpPR8HkbkPb0WK67piIATPIAPQ83ApPYtLVcU3H
VHWLjEAYjdYAgW4W6+3l1dmaYvHFNJq4Dcmw1EadvnGLbK3srK+uXz+9icdt
0O/4/OUF7DcA8e+PH17f3S56ZJN2uxlIl0eBjR5ujfxIFQuCtLtcKWXLittD
83sDSFDb7ATtsBcEupFPV6tk6VPJk0wW3ODp0+zpCb39w8NXp4nM6Umi2gr7
Q8j0dNoenaYDKmuMmjjucjvfnQWWHa/+QXA+sNQJyiivmYPCs3SjbWh0BNAY
94PhZDIYbS5f317d3oJofHwxHSyHrm23DYqkjZZTJ09rLra7m9f3bz7spw1/
+d83QORQv37+8QNlZDsKb6Kri9kwHPfJrgHUUYbEBWatm816KUtLK1ZNyvQp
/Z2DA0TTPT/sG3qJVlxpZpLHR8nEyWkqkUykU8XU8cHBwYtvvzsE10qj3Z9w
0jwekpEla2aZepOWb7eC7mTZ1aGLtAAsVjSpkauwPhPXkZB9wWQqaqOhQOzU
9Ck+mEwvbp/e31/uLik92y5H8+V4FIWBCX7oFl0UTW7P59vL64e3H+Jho682
4PNXG4D1f6RYYreNtPHNZj6aDC0VA5FStVSpQ4gVbrtWzKYpg81LDutjkO9y
W+3ACVqqQflmIZ0tFlKJ1Ek6fZTI5PLZTCF5cnz07V+/efHy6IiWD/wDGinz
SejYzF4PjTybfDaFtZMWtG92V9yjjjmPmBUC4EzUESahoYA7qoFMgUJ8Owz7
6835hw/329353evrm4vdGStfTCIPhH1kI1QF8zuiJsGz5r/uN2DvBuIX8JtY
/+vb1WbmDHaz3gSSfZYX+B49gSZtQ6NRiQcLM8VUWoV8GwoTvtftOp2J4w9L
+Uq2rJWS2ezJaeI0iWIeiu8HB6+AbjlK1N3BHK1RmPNpzzE0WVcg9gqkmNbq
dqz2YLoCQAXp41fIPsBg32L2cByaslqT6etUK4qimp4bkA+8frw+313fvLm7
vYqpLy+2lHTYJhpYphoNBt3J9hqYwh8/x6NmvwgyvfgJfLX+t7fbxWyx2cz7
3b5leGg60m9vm5IMSahquVzOp1Lo5TdyiuXgDpOnjhyyf61pB5X2Ktg40qkM
5jTJ3edSyRRdgFfw/1XoUJ2zFjbg8m0hM0VRSkNtSq4XjSLWqbjjIt0P8WBg
PBUIiatzCu8NVVNKhUodmtiK6wXTyeLs8mK1unqNaPhBaE8gKluPghYlFRRF
dsJWe7zZr//X51nDLxvwC7cAuHH87u6Mko7RIEQ87ocQwJ3hjVsyWb96hZlm
TnMpza4lclW6gmSFnHZLo3zT6tBKctXaYaJYKJcoFyoUixQPMzNm4pQef1H3
h0jqQL98wfIxTXpaVYzwyTXZCjvj6YjyIcbcfPoyF471fxLyZMuRb6h1uVEs
l/JVCvAtRoNRljRd3j/cP0umAbFKeVd/PhuEruX1eyBbuOCu+Vfr/3oDRA+I
139/sZrNBlG/16Egd8htT3BWdaymrDYqxRylsBTJ505TuZNkrlRVKGLzkbu6
Q9dyyZZZitSslRjuWS5j/ehupcEN2eSpcqZ7R14w6uiUpFEkDGBzTVP0NiW6
aybOYMK/z5/FV/31syjs3F1RcuupoK4CrSrmASg+97rz9foMxVShbPTxw0fw
NuG2bN5u6OA4fA+i5dnd03uumaJchG7X8wbs40BaPwpAl9vRdNobtr1Ovz8/
A2f6FfQBOhblK7UiBfipk5PTZq2SPjk6OsnXZceS6VFa7W7QiShgoHAeQOZm
FSlutVwB3j2Tz+XzFTos9MZBB3hxvp0Pfa1Rayrlar1ZrcpaU/HIMez2Ncr9
8cecIKzvuBp3bakuNcoSuAZq5OQdJxyBHv1BUIR9kXN69/b19cefdqNBr9vt
jadRON2CbESsn9t9X17Av6//9dX5ZDjpd3vBbEYh7j0LKZA9GfpqDShVcmrH
x0dyOXWcSKROs+VyQ6pTLO8FnQFlahOeF5hPR5EjlSs1yKeWitliiZLeBkV4
48UajP8X55CrdaVaXZUoTiqX6Ro09fZ4KuiOUaSI17+3fszCP+/7OnngfI2S
KDp/inHs7mR1IWCKz5pwMf7vzevPv95FvWiA/3W7QxiAD59+jq8693sF7OnL
+tE8ef94fTGjrDMaj1dcZXv3VihA0N2jUL5SSqcolX8BFYyjJMjf87lSUTak
Vi8Anz+PojGp+Khj1CoY4aUgtEResyxZ7Wg0o0CNxQFmw8CoFZoW6+uVUBDQ
/R6zffH694EKL/8Tq5OdLcehLVebUrGYzeZNBZILQizxSRTCvmgCcsDw+PZx
FkZoWA8gCjY/v318/z2XjH97vgGfYwvw694A/PDh6fZy0etEvdkS/BTkh8D6
cAd12aDtK6ViPpM8OTwqpFJQxU1TKJCjXSjrkCxeAQ16yXNo5IJHXZsChqbE
VVGjWqasrNNHd4w+8+mgYzeK+VqFfCWFCaVqtbEXhXvgHsVPcaAOWCaqiNdc
etAVVZcBpss5VlMBQyhjk0ReE69esAR+zywSvT7lz8MBM9+i5/qRUZP7hrfY
AF7/b/H6KQCAagjdmfnqAl0cUDe8Jbdyfb7oUZKO6Ifu/wl5QUS36QwYp9IF
hcK2GdSyhM79DSZCF8PQkhqS1GzUNcmo1ZpM+T+kmAmjib7dLBRLxVwW7LmF
ArkzMC4smfB336P8WUD6P7A2L7DcLbKtmlYu5YpZU5MNaD5gzvy9KOo8r59J
coHlm/VHQ0qJR/TP+Wx5cYcL8PPnf7sAn3/+/PkZBPALdwAvz4a9wWS8uiKP
GTcxHrlTHxhNuQKuo+Spoebz6XyJPX36tBpNILwF/R0An25vyf+eQSHKNkEa
Kus1hayE7rSDQCg0erYG1iQ6e/pHMpml51xmTczNmSjs8lDLT7EyI3hjWN/a
0RS5qtB7qpVcVTa7k/Xl7ZMgkRAjtM/rB5bx4ZIiYfqrO56Ox9PJhCzAmw9f
LsBvgnHq8+ev+He4A3h5PumRJVvjvvzwTLgIPBG9WPK8dOFTlk6GPc+8e6l8
vbvdXvI4Gi8fVbHbK+jehO1Al2XdqNP1psypZRvMsmJqUi2focWnKFJOAQaf
LVWLdQP2ccPUMQKc/YOg++fKJgiv7CCQdVWpUQBYd2XZBpyPsQA/sTPDy3/G
soJG6nw5GY/p/g8nZJpH/cUZ2Rb0TX/59esX8DnmX+IEgNZ/f7ZY9Ie90fIK
7wUimZ8AJ707XwxduVikECCbzpsmmM2LCPBTznKxPNvOoH10JajnsX6u/LUp
QnNbpoRRKEkBXwv5kFqpUCpkkpkMhciJYzKnZANytJlggycHeYn4lwkx48Ku
oDujLNsxbEMxtYbUtDRHk0HicIM5MWEq9+sXVuPTxzf3u9l4MkADfzKejIa9
4fri7undp69fAG/APgBGBMgd0OmS/OZwfsldzBj1CkQNZR8gm4Pkn+vplBVT
OFjMVifj0WYG7QVgHq/364c+wXC5HIYh5WymjnpFpzfyIGyTgwhAKZcGZ3A6
DdxPOl8mD8EakpBxYbq/tzw4janIS4ZRtkE6YdHlIYMi2ZQ8tIBmxvp/+hyH
iXtE488/M5RxPR4PuxFtwBiM3ogBrvgF7IOA30Qq8MvzDEm8fnrM/UE0QsT0
PZzpJx5Cvd7OI7sOJv9CoUAJplalGK9SKoTT/izyIWeLWtWVqIrfsgUcL6dD
3w9cQ9NbXifqhzq0jbKFeqGYzxczdPvJlJyc8vtHSCebHmSBz6EMytKnQn0O
43eUgugWWJB0Q28qDbOlKWY4Qaf9o1j/r8wf8dMXKO/Dxaw/7IYhOJ9pOf3A
jfAC3tEL+PnrF/BcB3++/9PutN/vTRb0uAQx6Q/cxzubD1pktHM5OvXpdOC2
XAsubDSZ+XpntBCjjLc317ecg0Eeehy5rcBzbc10ddN1XEWhwKWYA2Nfjtae
oMUfHR0fHmfyxQorI0AEfiC0qm6Ehh2lipsVyNwtmeJPRVMBM9ENy2pUFRdP
+omCms/7SPHnZyTvh6ebTT/qQYxl2IfFbbcdf7S8vI0p1wTd1p53K+4icwJ4
t5v4wbhjO2PeLWYwA+Ey9MVdCW++UK6t15PecDYdtCp2r2dXNFDVngk6JRz+
NaRft8vpALBl11BaNgjzy6U6VIOKhUI5lc0kTk4hBn10fJzI5vK0eqRCVQkV
EJ7rPr+8AF8ucBeDLqXgtD3kTSWNDEmTsnFVo4ByuLq8f/v9D5wqfClqkNfE
KBdFvaHvQxjTcxwHwp6dMfOtfv/DlzDot9+eMUC/xwnwZtzWe1292V8zRQ+m
Xz6wOPFi0FZQvi+WaxdYHGX9Xd/VZElWPYgWC67nPdkxC3p3O3T8Foh5MAHM
ajEA+GQSyXTyhI6fFg/e+FyuRNEyhfbNJoiHBNudUOgAiD5wDAUz9XXkimAY
sHRF1yXVBo0MWQDBoPiLwDHD+5Pzu1pCBdp1PN/xA6tlQYrb6s6210y7QyZT
rJ6xAwICJNb/5no1bFtmS5L9yfYSJC4f3gsc33YWuRSrG81ypQrzThmMrjmg
e1B0hxVGb5CCP7D2692VsFq+67QMcoKQVDYqFXo7hUKtkiLzT3FT8vQ0mUml
QfddrNTJRWogOJNUISQFLo8RBiM90RqUm3VFlzRXp+ek2pasKpY/WJzdUF7H
2UIcL8c4/k3fD9o2ZacOisVOSzNbhuHuXSb/hq/AXwwA4gLo4/Wi76Li3TTI
vzBQU0A1L1ajwGpWJcziSWCyBLQ71FS12VR0C8PQLGYey1QJqsNJ5LdsFy0D
VVbQkS5TQowuSBmD8FmUyskdQD6rRGmwrOkMqKYnDn6ZDjQ//XbLtloGtB51
y3dbumqZ5AXkwKtWaqbXx3oYDLSva3Kx5PFm2/cC2jgQDYKbTG3ZqqabJih+
r0E7GHvBr5cP8BgDQHoQYqmVavSLyRc9Pb5+ZIHted+zpJrUtJsNCxX5881y
FSmmZRq6YnR5VoT19V6z+CcoEcCcDdoMR2kwK4zb6TkFMBCDy6NYyEJCjpZO
DoWWj/E+MDmhHE73VQflitd2bVq+Y9uGbrb6LbofFEXpti5LbqWYLxtMZSF4
1GJ5CGBgnm5347bb6QRBdwixh36AjiD9WEd3BYDyA9+A/cPfHz+eP8y/H4aB
RGEWFBguOaDD8geBqbDspqw5TIhLHq5r09HQtzODCRMVx9p6rL4EAzAM6NV5
nl5XzXzVcvurcVWqliuVUgX6J2QREQ8UiyVQvUHMkU7eMkE14Lqttu/6HfQ6
QLhjmjbg1qZhUgRpGkqxpecL+ZoVjplrjOFmPMVKyT/FqhOyekG7S14JKkeL
cUi3B0qhqkZJwxkAhAyf+vVXsf7Y+/9M6d/NdhQ4UdjW682a7IN/mdw6hh6H
gd2QdRcC0abz4Q1vwHIc8Ok4IPM9jzlqBUntHUtEj0LHaHVDVaob9KUhe1VH
4cpsMTMAQDZkySlFapoW3U+YSfCwAnbuWO3Qp9vrucy3ZZl+CLS1Z1mupdhy
pWrl6ApVjI6YBxSDioy4JUs16kaB43G1Eb7obDUOcKPox2iUNTFAR7yZPX7q
b4iFMDfwcLXqt7u9jms2G9WK5FJEShn7ZjntBy25ogQ2yC7b/vfveQN28z5Z
WKfVbrd5shDLf8OECBS2XZ1tKGp1NasfUd5Wl21LNdr1umJB+Q06I6wQ1+/R
KwfazlT4hQLmB4Zd23Q9ctpg629TGO06bd+je0ZGzKGrLJV5nJ7SJrXdm3LW
+CQmVFEmHnidjut0IYgHvcc7YFBaYG8hT6SY/mC+u4k34EvtmwJIDABCf7kT
hb6jy+RwyMR0+uMp+SDwKFQqdbJQnt2yg0+IzDELM+mwpECn01sw4zUT3kB8
71ZE7RF928CrN2g3a2q7paotcLny3OR2A3IQjP5TdD7oQmFEh3oaRG5dh/4U
MAwGPgsWtMmQ2bYO3VPFtqWmUqpAq60AbI8RDBfMxHIv2vGzCPBFr8OzfoBH
PAKCHJAPaFkUNhh8A27EDOE+DuDB0e8/vAW/oR920P8nv0b+uNqEFrrvtXSg
O2qUplL8ZTkswkKZydmi32XuscFgxmQIjwyUwvnfcNwatTSkPY2mqkiGVtNQ
A6Ibhb4uiwMzggpikZBG8VsmMPd84uAasV0/CCD+ShcEQHToPIN3sV7TGmQ4
soVsqUSBk2SDpI1lN6HLHGA2w/XBwPX4lmkLwe3Vw8WyddW2Vb0NI3gfc0//
EoeMKDRQkDsLPdpwx4RES6NSL2fKGLtv1gqZTIH+pVhuSJrp/MSEMY+3F5tx
r49ZseEUonnM0v0sKosqV8dSZIgF1eoYD7AhbA/aFgQKsUzvfUyMzwBberUM
8WrTowKsOgBTNFTSBmNUjuaz2Ww8GLQaWr0CNg2U2KEVLNt+F09q3I+wXWSQ
3OGaOSg/fC9ItVYDNI2hFkz+Q0flJIbQ/RjPvtKNfsMxHsYaLMNQ6EuXAUjO
kY/KZ9LJXKbeSGWy7KnNn3+KGXN2M8qvhgP6w4dLQfnOhBH3nAAuxn0I2tUh
iVWl4L0V8kDhDes5vo3p9fFaILQHDilkuW03wNhBGxD0Nr3FwIdY8E5oF55j
qBBtUIkOvlApUzyVyZXrjXJTNloBfjOQwuRyo8U5+OUw6PiJkhfQttpkuA1Y
WND6IV67AUdhHOC/fx+LgPuGQ0FGsymjiJ+jyDxDEVoqiaZPs4h6X7ZSqylx
XY4u1nIwoDRzOBr3J8CK8dyXEJUFP35oK2RGy+VyjcI7sClCI/0equ9crWde
XKHB/ZpVHVfTHhj8Ap6vJQ8GYfPREjoid/cs2HorBJXbgIxX6fvhC6ZyVajF
+mRCfAuUI5YVTDGDI6ZWmVN/O3YsciIaGHRUCrNcCtgYQ8ej8O9YexlINh/s
ZnTdq/TTC8Us5SkUqSZTkLhKpBLJZIr+wHKlIcC275EVTwYjTIqOBgz7gmT6
3R3owSGP0HWVWqVUVuVSqVYzMRsGRLGg3tnzfv3wlazjzcVmPuiFIcYt8Fe3
4/f3ohyC/P6RfxEl3FJdrpAFzGSL2STFkbWqbIZ0xPQaJwOrNVpfCv4o5tBh
ZiPHtC2LswdFJafthuMFc90/vBbsQxdgS2lTAKaBbKNGdz8HvEaK1o4JikTy
5OQ0kThN5fJVRcOYtZgypqwQZHP06Q7Q3RFaP3T480k/dBRomReVZq5YlljO
4xJyHnwvf4gnEH+KRb0+ClWz3QLwXYj0hCFlTwOmIXkTM3V+jIkd0D2FBGOe
Pzw3lDPKlCNWpbriDjf92TmTS4v2+Udev2tA9oXJLS0yqB4Fo/PF8vyM5ZlY
l6MXWAoIYCm+b5bLlRwkzRK07kQ2fZLE8k+5rZsp6zY3C1FkebjajAfgG+z1
w3C4WO8uzs+YzGc6jAJbrkn1Rp5eUYEuQZvlXHiUlmk3fv75Szd2r2vH42Kj
Qbfbi+jvfthfxQVhwVTFXByPFHqvxqEh18j4cTE8C7J8t9Fwa3RwlWrNmwA+
LcgVeRia7v8IiRi5Pw2JSAuJIcWH64vrxXIFuwqd4hY4HymYlyV+ACV07hKn
tOosNK5OjhPHhwdHidNEJl+Oqbo/Yhp6MRqPafl0aChf4cdhKKDX8XToH9br
hQwtv1AC5fBW0NagVbXnfeXZqxi9DotyRzFFrw+Vqv5w0ANIXgig7eUvUYq5
Q+DlqNUyRQE4+3Qql9M1igS0AuURTau/5CFB0RThYfDrzQAlABPTyppqmL7f
Ij/TPd9dQFJ6uRhR9KHT8pljBQEphSu0AZSknp5mkrns8cnhwauDg1cvD46O
jrPZKuLFz4KtVFyAbleQj5IhQNLa9dsYia9B/7KQzVGsVtI7oFy+E93dH3+M
ae/34ff+QtGGni/6PdynIX02V2gH7tUf+ZaAgQAgd1+lSLoC7m+6X7lauyIp
FbdUrsuKD+Mn0D5YP1oBV6ueB6cK4XQDYAuPoqtgNZ1u0K8Mej1LB/F3o96Q
oF1ImwiwS4MMLC58Mn1yfPjy5UvswCu6Ajn7dw6ZeGsx3tRDoQnSWr7H2haU
I6jNcrMO4qNyHuWdUlnzmS8rxiD/HFdh9+jLeACN+U83IyjVYdByCicmSKKF
+huzlIgZ9I7epDC4VgXcoFDwdKlZa+h2rSmZ/eU5/THxriGse3N/uYwwPuYh
rKRkyum1nKA730yHM4ibIi6l+Iw8FYBelIjS0alyXZFqpSJl6alEJnl8fAS9
nFcvXrw6eJVvMtHCL0Ku5HI9CkJ2WeS0bPYxZGUkqV5tNrKlItj+0uVaRW0j
m9wPYMb1h9/+bf7glz37Px0KGF2Hy3iSKB7WFFAILkZvJoGtmlWKKygOKsvB
yKDNUJqeKakc+b15FyN9RSvsfBH6FMS6kHF1nU5vEPqDKYUbk0kvsA3HpgSl
CfaCWh3snJjGYViaBTbwRiWfTZwcH796+fLFK9yCV4fHgmjgM3PmUAwENBvC
Ng+Uq2BAq6A/W1EDhYKoYqHWKNSrksuc26/joCuuQX+Nv0f9leU/6EINhuPp
dLQW9W3Ro43XzzNFN7tZaLa0Jn3hckUPotk48q26rGqBwq+fmUV//GlPKnu3
myKaoCTK9fxONJ8Pu+PxYDIbz6ft2QAq6pi/orOn2K5abSimA8wrJp06bdDo
1otZrlW+enn44rtXr45O/hGfFzhjMN9GRw86eA98o+h6V2Gaq7VGx6+XStlI
KTWkhoWZXtZ84PXHZfffv+DvMYH1A0iY1oMg7A0pPdyiZ/vDF4psIREEWqyz
eddr2yDWq0P0dbGYjbqUQitBy6PX/7AXjeT1v0NSD74GsLdRdBXOF7Pxcjbs
j1bDURQFhkyWqgHNRiC86tBmhzLElDNUCkdYJbMEqh5a/ys8g8N41JbPi2Kg
GQ8n2BY9+0YNwrgUPYADKF+feMWiGtWkhtxQg9FqJ4ir4iXFw4e/xwxOYn4N
9OejAONlg9GOWSC/Wv9nxoJh/bMIGlKWoVgRomMKOEaBAVrCaHkRYwjQDRLu
73rdb7e7FFd2IoxvLuar7Xo6HVB47vcoIIDhoyQFos31puF1B2MWS8bkIwSi
QSNqqfXcyaujg4Ojl0eHvH4xa0y7+3h/sRq6ogykKbx+LvSWC0W7OxhIlR6F
AQ2lqTrRjMlL3ou8az99LK7A7/yifkK3+Wo9pvikHYS0fj7/PUW2oDgT93/a
4/ds2eFkjUEUCpx6LdV2PECdnt4KyWCwGjGrzSJCMt3mmzKfLcjjbSeUiE4G
Yd8zKKullaOxWFcU2+8xr3UsE362WyM1peBAbxYTRycQ1jo8OPmHuAB4sNCr
2U5DuwXScY1eP7lliKJXGxXFj0ah6VgNmYIOTdNhATnvFOC2Pe7it9/ZC7JB
wWO9XA9BX+20B5vrf9PH2jvAx9ur7aQPALFpYq7v5h7lyNXAa3l+b8EcH2LO
RyABnu7OZwFI5iKMbJ2d7Vbr3WS9WexWEG5QyexVQV/TbMgKBKdA63wpOGWh
NQQlTGCvXUMqJemDSY7MP8QFgAXA9ToH5tS1DMxMSGT8SkWyfw3dVGVUNHQT
+C6TQusOk94yA8lP+xncfRmWiVuA9MEAXyfw2mEQLdGwEwOrcX8bAdB72vLV
cND2LU11R0xS9PhAVqjXopiOQr9nBEEc/dDz5wvVne8uUHM4B0fwerud9duU
E8oSmNarDUAVJBvEoqyLISq5opMHuGY/ZHHeQp4ConxBTFv/zi4AVRNyATbI
YluOpSgyVODlpuGQsQ0cx3Mx3EE3s+WGwwkGMRDSfPpxDz7bN2OBc+NG425O
wQqlf057KlpQYmiHeXoRJH8gC7jsd/yObbZ64GbBBMzdxRLpL45fMFvHtF4M
BFj1wSEz2TKfJR3qFrov5AQ6jgmWrkoDaCpVYs3VNXIUQfz45pGJJJGZUyof
ukYTJH7FcqnIFptLxnwBbi/JBdBdjLpQwgEJLIgK2ygNLaZuqzPudv1w1Can
M5yJDfiwl7T+/JVv+/ETMgBoDIDtottv99asIyCEBD7F3H6PFCPeLnyHTH2r
A2NPueEbisOnbbvdHm8uecafl8+FDXj/ZdcL/D4kH9BUfbg5P9/wpYaAJ8WQ
YO1rUtCvtXtcn3h4eC3KE2KECzKgq9koChytDvV2sm98+r9zzMZkQ9dnYPe2
gg46FIqJNp0dROg871aRa3ZMuxsMR8PpKKQgAEOFb1nUNO7Y/yzo7wXSBxIx
Hl6LE/a6kx3rXz7LqKHCef9IKeY8GjluxxOvndZPTmhgum445+Hb/ZwLW0uQ
KPbC3oh/lqDzvLrYbcDy4rnk+xtovDXIdyqtLsa6bu9ePz3F6m9vMVtFTwBU
qoOwbcpgsKYM63n9wIwhBiCD1LUosXRsXYO8O717UKGsttvVfNgGp23bjcbD
breDysv1HeD4HwVkj4mYhLA9ajA7FNUxFoJecH+2u2INmngGlStLN+eXl/PF
NOz0fMiIYEDz6f5i6Sttd7S6fHj2fTEOhJKfISWn0fziTpTnwDN9ebmaL/r9
yNPrDZ67NExFh+LwxY1QrXwXq77Rr767Rj4/hRPQ8FJoA2LSgN84ZuWx24v1
iK4kiFENlJhsvU1h+OXlDV0e8sy9fkCPYb5cTqIQJcALMNC+ibWVPsUiWSyR
cb6edG1aPD2iVtfv9eai+PMgGou33FZaXV2sZoPxeNxFneMRNAI326Fh2j7r
TnC6yNBxIEcpnqTgv+0Gax4Y5CLKw/XF1WY4iShs69rI+VTd0GU7mq7ExDf9
Kqi3CKlNlOZo/bNxv0PXBfzltaaYuY7HrpEGMsuD56Bu29J122mZfUwc0o4D
uDkYTCicGw4pUR70O+SFGePA1VJW2eMymOgprWc919A7kWWrhg+NFYYDADQN
WutzWv1sNJzMJ4Px7OqiyzIqdKbk4X3dNvpibv6TQM4LNR3QZ3favtulYEJw
bcNaXl4sKfT3HVujmEWjI2tZenswAzUwbfSbd0L0C3MXrFon1t+liLNerdEW
/PoMohKVMMBzMejptVstj7xgy2iNYJlAcQDkACXFI2iOd7tRFHpCU+SCOaUe
WdhRyP9CHmvWQ9GT/vZQqiXvGQ5j9Q0IcCxX40FE+fWIgtPpdh2MNnyor+n4
Tdtyxht2mD/s5bJF7WszREuhT0lhXHRFR4A2euS2PVMlw68ZuuXa9GBZ/ZLu
2VOsjPLx/SMmPM9RI6A4sEsPgEHwNYEaATpZFC7eP71mvjn06FqmQb4QvgsF
2A/vOVoVxWnK67sdcontaAialN3F1c01z9e+Zs7qSzrcfsdxNKvptjRDkhxb
lXQv7OOuczTemy/aKDJAjmO8HC52UJl4AjgrMFpmQNdfEKPG4Mn4+tO5BN4U
N+XtfpwIY6sTSogwUITQjHJAFyNd6GG9ZggmQx8p1L6/QXEMqhK0frJuDQA5
4smEzyIm5VIwJIR6noMpdRA1hPNzRk8ISZMtLn4vCikG76IM4flRH6oq2x1C
rRsepOP6d+Q6LUWTFfpeUqWiOnqj3NBbTH6FHNPs9LtDP+yRa+mPp3TbH64p
+IEql2W1W+QNEF3uA0ZuhT9RqBz4rt9eXoti7wehR0EvbdTxIdyGdrtFoUsw
WCBAeE0+/0nUZwWPJqAM5CyhJuAgwAeYN4ZOCwSx0K0VCAHg+9qR6zvhAoh7
/JSPXH/og8kOZFKdDhq4hs1dwBgyTEHpVuitu7ZjKoahWaYs6zoMUylXqDRU
/siS22p4i0FvEA36ZE2Wu7u7qwdyUOeLjtt1naGw/vt6CT9MziaDoN3Z3DLn
dczLxUXUbttvmapGmb7lQNBgCVbtL+uH1DjaAgxmnEJPA+l9E+H9Hmv6E4Nt
BUrz/goQgZblgjOtHS4v9iwQIGM8mw5nw7DthVHX1XVDpXQIGgKQLxHaLbMJ
7EvLQu9fIx9CAYmmU9qkl/LpVKYE/txyrUUPtTcZDMDGBfWHyyv0UsCh44Qj
vz3ZXiHxj58/A0HoT571+v1ep3d2F6sI0xYwofVmFmHCVScLaFmW3hLDJ1+v
/wdB4EP+75ztXwSVK6laKZQE1lzwBgNuvRevGHVajueDNqmzuIgr8JyBXa3G
owkGOH3PwEk26uW6pNM76HRB8NfrIjunKNkECkBtYnizIulyXVEBOMwXioV0
pdJwFKMbdoP+BO3jzdUtrZ4+d5ernt0ZuB3h/fbYYcR+EGwj5zPqh2OKJAWs
kpmVUWknT9OJWNJA00zVHczXcMvo3zy+F4ynsVPmIefllA4ogJ5GIZv/9ClW
ztnL+30ASvdit+i6FJQ6aFvOhIAHi2vQMewW89F0CDCcpsnQaIMURq2p6Cak
JWy3ZVD2rAs2QZTgKI9sKJVKHVUEugBlSZZrNcVQXM92/dlqNe5PuDHyGqrx
c3Aqmd358/p/ElNjb/n4B4PxZDDH83/PWrSAM72+BS+b7/dwpSh3d832UEjR
P9LjeOD4nMvNmCQQLmAB3gPyAPVcJhuLluyjcpb3pLDy/HLQdl0yt50onOxE
DfpHcQHoB0woC0XOCjQA5Zz1ehl5MoBftWrTkMGfpdHDoP8IrF+12CiXKmYt
m88XAI+q6pbSkDEZ77iD882oizIfvu3DzXZkS3rLjuZnorwWZ0tcnFwNoeUy
Gy0F768QYxWSdzPQ2LDmHVlsswNSCVx/dG+fBEkkKyO95Rdwxvap23H1Rj6Z
iDVhWdv1417flzKl3a7b6gRuQNd5vIX/E9uIHJl+wMD3XMs0lTp4kkuVBpAv
ZN7y2UK5oSAI1RTA5SkYl+vVcrORyxdrRay+Vq1LzZqSz2kORRaRY9DrX8wE
j+Lj3eUioJDLduL1P3NiwPPupr3xiHzleH37CLUEprPmJeH8KTlt0fsn62+a
XR69w/pxATiFErIQdLIQbt2tOQTyTKmYPCUvClxcnJVwA/ORw5cFiPKCTtDt
DLc3e74NzhDONnNmTDQMqd6sltBaRQObVlcsl6t06SVFUVWJe+W1WrVQqWRy
ZPjoouRKdUlz6rlErtw0LCgw2+1eF9hHWhJC34Hney1VsIY9m272yefkLFBK
Hk+2d497KdOPQop0Pe2h163B+tlGqye8/yP0LO7v38UXgDlsxAWgTGYypBBQ
KSePMBbzjkPXd7FCOMPUd8th0PVd8NR2epi4YbY5+jZQV1r2ySy49EdRaK+0
pHQ+k0rT4Rby6A40VYAfyTTUS/Rv9Oppb/LpdK5aq9SgGlOVMyUyFa4DmcU2
yrOoDTxx5jMfdM0m8PBMcPc2Vmvltv96FLKix2h6dhcrfoAenu//eho5HteQ
ALpz+7Ov1n/7iG/Oo0S4AI/3N5dIGdEls5VS4oj5cN4+f96gUiDGpMKgEwbo
30WrK670CCI8tDUmdDM8Co1lybTb9SSkLLO5XC5fh0SEpFYrUHholIuFcrNW
hlRIJku3oF6uFYr5ZIaev0UeUdYltdciIyMyv6cHMvAthcxGzYqY3lcw28Mg
PdAVj3pMVT6YnMeoeu6iIgAgbx2hIWIYumZYmjfgRjP692A64vVjAiGmlmET
uJyNer4tl05fPa9/z430+IAS3HrWR+GKoppZ2JldIhhjiSG04G9388hpdyiF
kDXXbOWT+Qy4CTO5XFXGVEBDkKJUK0X6f/Dsc5lkqV5l1b9aJlsuZZOZAkJC
TQUssL+CxjBlV9uJVZNVqVo3QfDIwib8IJ8gpDcAfS3G8sgbfd1FfiPwrC3H
wTi/Si7QH4CZmtf/+BqU10gAhW+LpZvJB85HvbYtF1On4MQSSTnPWwrBEXr+
0z6IAsdt2oTe5IybPTh/6MvdXayHg2GbwZimpWN0JgVa6Gw2Q1aQ3UAVIPBS
PpNIlwulQiFbrMmV/EmpUi1l8gUKA6AJqVqq7LR8VHPo295TauEr5D+KxYoO
ZjCGlrzh54hwJGjRWwzDoIei+FN8AT5Ai/P+ajfv2rR+XQcroR5w8sMILrr+
LA36UWTm/F5gARjP1PEa+UweqJU3+w/wbq+ZhIXO3wc/k+9Ar3p9/Rh3rr8X
dT1KYPouBPR0o17Ip9IAVgDAkCvkSmToihUAIss52pVCs5rPFcpKqXh6kiw2
alnQxtTrda1WkyTDtTrDweIMxQVaBEWTxWKhVFJ8rt7cMwSTA9xJ1225TOE6
WAoxtv3bYPDejNZv0+1Xye0YHZAx3cZyPneoKbK2DhsAYQGRnZH9c6X06dHT
41c78MQMFfHM02DUJttHlt6LlpfPGpjolN+czekC9B2TdqBZhEREMpkCXQYw
oBTg0hmW4e1SyUxNalTK9K/VfOr0NJXI1iHzW6qpdUoKIY1HQSDmE8/Jp0AL
vIE2a7nh9DA/xXhVxOyw75QUWSjDDnmsnPO/D0KP8P76bNZptSyQDqnNBvTY
OPl9fBLoNY4WY/aF+PyB5wodtZk6OWSY5xP+jm+/EBxaTUezGVdVyLIiAn4r
RGA/iQewGnTDqOMAhtmsFnLpRCqTzaWz5Omh5F2iS5/LFnPJxGmB4uNis1lJ
J06OXx2lKAFqUlhUbmpK4HTJCVPUPOxNFsvFNDItGfrQtFs1CmEWWzGFIsaP
XEV2VZXcuzdicBaXnGK4Ec7fR51GVRB0YJjsLBbjwmO+pkyKLSkHd8IDAvMf
2Eole3wkYN6PAuz6KPDOV2fb5WS4XlFWBVabtk8+5w0rLQgmOArFR2HbJR/o
mQqUsiqFbLoABI8kVaR6uZTLl/O0HcnjtNzULPIE6UTi9PgwWWoAlkIpimJb
HZ9S/7kXjQdACPQCo9qoFKCslsvnZQ+cHJRNAoCypFSaLotSqzV1wxsyleFr
kJg/r38zclowf6zSQ+tffVn//c315c0j0IMf99L1twxnjTyjkSukkiw5J7De
IAd7YA1ECHgNN4vIbdmmSanVcHPz+PbL+h+uNtNOOwjArKtC86YhyXUy86l0
rVRX6oDzFHL5RCJ5VPCUfFM+OT49Pk2lT7M1BZxfPqX/TkhH7zuDwWDY7dJT
tOVKRasUYTsAMjBAWLpYrbll1XWVehMkMLR7rgBy79eP9393tYlsMkY6Q0Il
sxvffzYeFMpcUGLNhef3rBANJi9oYLWU8mm2kLq951f2EAMY0VNAkjybDAez
AbjcVNPp9BaXcQSABImxYr3RINR103GVZrXcqCnNfI7eP0hK6vSKa41MCg22
00Lq+PTw8Pj46CRFlk8y3SCMoOw6iii2DjrtTtSnlM4zNancsBswDuQ0c5mG
FdDtmM6mI5TqIDtD7rRalw2sn1Wfnt4K74gK4LprtiDniXEiyQjHS0iKxeu/
u7m4EOpqLCyHKTQ6/hEdv1w6SWTS6I7d4YNhF7TJrhjxNqbApzuJXBtKiGSj
zhBHsBXl9Z9NRoORJ6kGBZwyxXwNjYxpmXJAGGFkelWKCRMnJ0dHqST98/jk
JJnLpsqqg1bCZDKZzga9LgPDcPd9z7YbVXo4Zbo3uUIml81Lphd0oyjCgGmt
IkHJm6IHSWn151vA01+LChjHv5eLjmE5GDcwNFMi54mqNBo/grj+6vz6QewX
ls/HP+lFngRF4YMMxnwhOcnDrhBdBA/kYhL1onYQUgigkr1ynD7wCx9jYDqQ
PevlcNimeEOjpKuYKVTLvlKUzZYHwWJbI8eazubJK5wmQJZ8fHpymi6kkzXD
6w4nPDi9mqMbHYGRuQdZQr1eAUyzSO8mk85kU7mGRuaeg+RyDZM5EuxKvWaK
2sY9q9m/w3t+TdFKzwSuniczUPsHN4WgO33N4xtntBtM/gl7gGmeEUW21fTp
8dHxMcs7XF0zlwdzwyI7GNM3A2a9ZaiK3GiqWjA/v3/Ds6wf4/XPaf02PbhG
uZLH2FO1ibHwqD8AwaOj1bIUFfNoVOIkzZOhuVSqZvi90Xy13my3u80a2LJ+
D3jxDswo+c1SkWKjbOqUnSmUt+RmvZQpyXIDH3oB9YoKVtIrFDcE7hbzPJfn
cx0cMZoqqaassBhhzDgVj28AHPmIeojQkhv3XCcop4+/+etfvt2dkZXFsDuz
A6OhiuSQTBvPO8mSrFFCJ7uT3Y3IOpAhUza2pF+j2826hDl6ECFm67rLPDrT
6UTE1kmsOZFKJxNpMgS0FykARycgTjhnImJUYoZcR25D3rgEohHk0MlEMg2g
bi4PxolUplhlLE+NYspioy04CRl3DFptYH3XU8No2bBVqq4rHohrL274AoB3
E4KMGGi6571gKT3ftO3kq8ODl6ev+DS2O+jugm8HBnfQ9R3LC8ijaka9YQD9
ZA7XZAGFCDJGqCFJoTC2NIfpn2w6RS8WzAGL5Qpcj6Oep9fS6TxCI4Btk4kU
3eua1RnM19sLBmriqu3WFIj0wnbbMqVGrVhimhFANelD4WIql6PI8jSRKkKH
FIJE+bKF2jaWI9hMATTdLAZWq92OBhQAGLbWYgNwxQBeLsaTv8fvAMWdkDcO
LMVsJr795q9Z7SVqlvQcydXEYrsj+j4ORrXInqBupzbI+aid2dktp13vBYHT
fOCTXSpTiseYTch9MeBgvQVvEfmPYceWuDKA7CCbyqRpo6pWOFoAknDNtgaj
lWccirmWqdWRIUFbM8uLP02ekM9Ip05OT05O0kX+UHBZlkE9cx6/ACS412eL
UdSiyDg0G5KkG02zM2CxGzHAzciHXTzRK4T/6HLKjew3L16lK8VvuKQwJYOM
iwsJJCQZFPZgakGleKqKJqGsO0P0p1hEEBOUu3nfUzE0TCYLxAmU58iQ82O4
CWwoBVA9T6VYpljOA3OeTGUrxQpKU+Jo4HFub7lXQMFY37dkWn8ZIwAV+oF0
ZU6OyYEmToBTOU2dJLKARqZz+VoDuo87obb6+hHujbL/rmt5IG6UmuSNNQRP
2wsm+8TkLda/ExCY7ZLyPt+iF1367i9/zWQyh3/phDz20SenTN4Gw1bk+DDq
a4MGWa7WK/C7LScCgBVGB+ysl5tZz1PKlXKF7n8mCb2HgmSHgBxgdZj25QxK
pzWTQ6cLfZrM0k7qHWYbjamoH4QU4QUsUuRpzEklyZQu5TKZ1CkWTjtwenRM
Pz/B2PV8EfNmrWhKCcMVe21aG4SObZ38g84SheUyfRE6CPoVTCF1C4d+toFW
2XoF4UvPJI9SyxzlZCXz6i//ZbuuF48ngamRfG53ANkADzrhSlN1MSgoWW2/
T4kX15QfwCEyjVypTJlMNpvO506TtP6mJe4dj46yZuViFFr1WrlcohedTOfK
jaoqcjN2zUIr9wFCx+BEHIUtkBOqNUDBIaubINeBLSDrcZIA7VCakstKnX5N
K8KMOrPvnO0olO0Yhm1IqlXNFQqUYlfoAoCeBlSn8GywM5vFHNSTw6jjarVc
qZytm5aRe/nff/6T6Tkm5N5ZHoTOvweSrW6XJbpcQ20PQkNWJCvyXJAc86bT
4S7p6zZKGFyhL0ZHQ1l9VW/3me/uVvidWwyrde1GPlfMQeg7TzGczKqFzPX6
JKi4QS2LoRmEpL4GBiGeqETwRMvHy0lBJBwEPBQaFBtqkzyy6XXHCz7R+WzW
d9GBCjxdxWWk1LooO2Ef0k074dbo2pOvnc2m417oWaosNbKnxVI69eq7v/zx
D39qYZqY5X1B/RcGUW/WA2Y76o76kRdS4ukqLb9NuZ5PeSpHCyBE6AdmrVIq
UNJHiT+XPwowAIvtuai8MtMjJ66NbKWczmRyxXKjKUEO45r5rdAqFjuAkRmK
Sui6dC2w7JTJDObgMpKgZckkEsW6rFstW29SZkzZFiX5eqsdgcZ03I+6ITlQ
xImWUslhGLNRaUB5d0LZA6vJAyK1pF867IdtW9OB68xmc68SzfKLw//8rz/a
josRRoB+eU43BL6ETCHCmHA0JtNiKIYVgK84GNP7Zm36+YhykkrT1qqYWqH4
J5NNp2sGLgBd7weRTHMZcT5w65iUzqH+J0v2gNfPBbd3McMX74AQnu97ElKg
UilPB3+KqgK9g5JkiBFiz5DqgDfLII+wnCAMIe8+XSwmtDavpeTzpXK5Wq8V
GzpzZS3h1CiFWs5p9b3Qdyg8gHR7gZL1Uk2uHL788x//23baEAhBXzbs98H8
BN3Y6RgTjaP5BLrbltfWdQw0InpZ8I/r+0azJltBxyzWC2AOolAnh+m1PSQG
QAChMNlz8ODIVFbpy5sYLrwXbJjvQO/11Q5AkXToK4UyXSyKnRNQ1DxNJHOS
2UZgNaaEy1UVnVIBzJaamIDQO1MGzA6iTtssFhE/4gKVKRaLpevmkMCbAMbv
+G6F7GPxNJvONeuFSu7g6NsXf/mLg+FMn2GyCMzFluGzWi4pNpgMQorokVlQ
aOG2KVvjSXbfVuqNWqmmttR6FdaKLsFpSbwAcD7GJVWmuuxj1r6KLolqGOFM
4KAEKIkJzuIxU2Eyhx0dQ9X5DJm+o8Ojo2S6ooMieU7BCQg6dRlRroHBJ10B
ELM/5Vo+HQdnD1nagEap1GDeWkALcI49dDtNDNNpUiaZLdTKcr548pdvD4++
edlyoX7BKNktv5dz+pxxNAgu1jFtLV08U5dl1bJtTLRhKsBEVET2ulGWm+Th
KWDPZxPJiuqSYRKc4SI45+ZU1G6AvrlO39sWw4yUSiAfj/sNbApFpoINMMqV
Wo6SoNTJ0eHJaaphQ4lkvQU37HwYUIqnoudsQK9MN1Qzwq6w3SjBHOdKFEJU
aK9tyt94+oZyHXKusgOMtaY0MmlJImudPniVkZLfnoTYWywd6t0wmPGHuc02
N+sZuGN9CxqgmmEzHzEyjUZDbjYp56mWJZBgsBNgFWgwusMEfMlOt+OOXqUs
UlJUE/yFYv37dhM2IDaE97c3zE9nQnY2m04cHR2dHGUktwslstWKQhoQx+q0
AZLcBA+DSsm5bPl6DbymVUyQpNO0c3kYwYpkYDbb81wMoXlKs237lZxBAUQq
X0slKWQv1DOHB4ciZOUMSKSA8Qd2/uLsarecwR0GlNZTdOmAH8XWFYWl0mSp
Wa9V6uVcNpNlCrHjdF33ItjAO25RvudBsIvVuI2WmAIELeJIoUEoNuAdW8F4
AzBqu8USiwUYAFiA4zTlcyAkw7gh2lIjD9rRuqwg+eYROLnZAOFIrVaiwAlj
TrlSU23WJE3SNYO2gII507FUzWqV60Ylk81lcpnTVK6YPTk8zRTWfPIMy2K2
FwEWZiALD/SCgdT3IttQJNnEiHhIDgHDV5oOEpNGHTlAnsLTJML2TA0bwGry
PI4odAMWfZsCc0ztt1vR6iLWYPyyAfH6H/dPAIqylFQmDjL5ck3hgJ+Rc/es
BEopLibsodKlAoytAWHXbDQkTLig4pDKl2kDJEUDIqTTcQwy3prWMPUGJdLZ
gtTUq3RJSslUsaEYdPaXfPTPhSAKShE1C6UYnv1s2zYYTtueE/RDrrTRH4/x
SxlCL2XMVxXIBpwkEkcZ8oI9CLPfixfwjtUBJwEPxIMGoru8uI01KBnAINYf
bwC3Z8kNumDnyWQzZUoZVQ/q9AIfcH99vhq6MvML0P3XIVlHJ4EeM0VIJUqd
k5QzUahV1RQZLNf0BjzL0MFPLqmaVCsWs7VKs5HKVJRqSTYdLwAj/mW8elEK
RBkQgTnD9Oj8QVdmQq55CO2CTgtT+5g90w3T0GWJcvMauGSTp0dHlK/QBni9
CbNf4ga8Exdg4JDxgOyRH8zOGNX+9fqfLwDKVZegB7QqlDkWqpVCUdNsHhy9
YxA3mGN9BeAKNLvoGtDfdA0buABlikTICDMHWbVaa0C4WIfjpjxONR1wlZVR
Xa2mT4uFki7pLgV7/fjq8/If4g9vAE9/nu9WoH7pYIar7/kguNcZFkq32dJB
Iy5XQB5VzKeODg5eHRydnGTIBnAH+v5R+HcwmI4DA715aJGNeahFqD083//9
+lnsfjMfeCole+lyo1Inq9nZF3Q52xsHKjQ6Ddw+8gISBpxsyJcqtUI6Szld
mnJoCT1IittwU1EToZvSlOuYMswWs8cHR2WJUpouwHgX/PBvudcSU76IDdhX
QieDjm1PVqtIqfbORz2cvEo7gLuM2e6WQS+gmEkcHyTTBy8OKFvPUCbQmzL1
M2uNwAfO0aC0W2670xluIIj2v9b/9Lx+iJ2vcAEwqpzIF8r1ps01vxtcSghj
+Cp45jWNrDDgVyZ0RECMZCqQ3cpQKlLM0WOoyjLIZqBqChoWJn2lvC+fRVEh
J9t+hABpeoksEaWC5zYAF8JvUSw53zKSraXrwWJiyzIYB0CaoKkmNm8yERWD
tqWUKF89PDp+9fLomCK2Km4AJmQ50XnNEx20VZ7r+WE4YCT8+w//2wFyGIgx
BTRfe66UAzMlJbwUODiAziL1uDzfIJwyNElWda72a6BOj3qUsfqOoVQp1crn
8jl6AWQCNbonlksX36Q3IOtSDTSeiVQpn6JY3Y+GU0zMXu5Pf98DYbUPzstR
CB6D96fVitYd2nBZkhUu+Tr8m0WUOJ+Nh11PryZPk8nTg4Njci2FGuPvyWjz
D+Vb24HqotsOo94CQ217/Nq/P3/ae8FHBMFXcgHVulSpl7IcAiGd2awppzab
KgRqNVqeAkjpUEByQwz2lFJJgIxAq0z+33JaFN1boGJSTb2Jak65Ws7TM2k6
XcDu6PtfXovTfx23wfgC8PJ3lDWOelHgBL6/npuivcTTP36P08vdPkzESEFb
K5NPpaQlV8yX6nUKTGdoYcZUHmvo7NIG+J1ub445D9G9/N/H/8DrhwsMjBLo
KfO5DN3mbFmDlPKUQnk0g6SGIoO7Aiws3eFkCoVvCFQjBcxXhCxLs1oHGMZt
B57nQNyXfERVd9RirdpMJ9FgG83QX4rX//AQNwGBGRTLP0OPGG3ObrvV24U6
rV/B+nXDG8xYriOOFi/OOSOMPClPESjF3+VKo4ZqQFwNuWOfFgXtNoRGg85k
e4OO5B5u9DbOAJ5itiWkAfMRRcGFXJrCtAwdaDaRhRY5ijNAbVEY1WxIuknL
70GkcbFcLKYjBvVXmk4xA2YqCs0t0+Z+BIDMlq2Sw6upSq1ckkrJHK1/PMf1
X10y19m+C7rHL7MaxAiMFb7ve/52we4G66fMo0tJztmFQLKLMAGguhki92KF
It1as14tVikbnqFQh/8O6U/fcx0oZbhDFi8Ffjc+/mfjx3/2Ne4/nX+5mM4U
j0/SmXQ2lcimMlV0m2zKfFTH08uNJqXBKAIsULoF6Qplqo5Wret1Wj8lnFVJ
MVl0BulP0O20VZCgNMu1Ql5LppourX9G9m/JBH2x6Wffx5RvZ+gQd2jp/UE/
6sy3gYrjp/WT1XHA7nvJaxfRItpGTITcs2tVGVXIOrjRaAMwgAZlMfCHtQPo
AtGrxaATUCnv3z+vP377XK5G6XA6CPRyOV2pnyYoXC2WU5CbALKgVC6WKRFr
Wc1qVXGEPjkSI+gQ0PqNZlWqFlAGqdQpXoOuwWq1onx91PMp9dFaSilTziRO
/v+erqw9bWSJ/u/J2IBAIAHa9xW0gQRix+AttvF44iRzf9St08LJlwf7xVKr
u6vOqeWUaKXL7fFYE11FSIedAOQHYPkQu0Sb2GG9mheL3X69PLycMqIbUdCY
Pwhvvf3zBy0yvMQins+nbUFIBOUvkDQCEtyjKhoiyrs6y9LIdVwvXLKJaGwe
xnX9bO+Z34HXfXt5uFvPQ10beqEuySOBkLpATl2TxMFwpOheSrjfM71kuad7
2Mg0P96faP8zclDEyDTTVb1ssdkx8UE22QMtL6mXFZapqMawzytE1La7FZnV
55fL5Yp/mEwjXXwUiG5P9wc6ANvjtqy/Py4z4n/orIb1n7GBYU1xRoMa2MbB
bp23hWdrsqaxd7XjgswTrhn0cGjzbRYFmR0wv4+F0q/Wj5D/dfksHEyPr3NP
VodWYIjDsarz/fFYBrsfjceq61sEZUw7KlnvBWPrzxjriTGRgDsmEeCooFd/
eHlv7ucba/oqE8/VbdtSJFkn61iCHTMJo9e362VuAqos/7Uh2lNXOf1Unl7W
BfmW0CfGG2G+SZNf/GyS5r9/fflMcJfzJrPJcElkurrtkRnlCC7cnY7bejaZ
xBa5Bk3H8Pp/f14jBFeR+19foBtX7/G0XSSWRGDG0saipIsjBNk008F0Vc33
jCAKbDdfHe+boZ7o62x22DcM2iZTtua0+/cvrILmk2k4P9ztlgVdYd1E9E8S
xu6UnNH2cHc4Y/Yj4h4sVvjwgCjDsljWs6LY5sv1fP/6VMTFmgwoKO9kNsk3
56erQiIEV/77cpo/MST+ro5MZESIvLU5UfeTGaJq67rMCK450DhSg+rwfMEw
umvB4f/+Y4aPUQ6CnEi/rmaRJpMBVC2mTGy5wNjEuPxGiT10HCdiDY4X5n9Y
QedmOZu4qmi6hmHE2P7vAGC/2Kh3VvVPOC2J7DAYdbneoD80g6xabferHVlB
ZO2emHrIYXuG3M26xHyiIk0X6+dLncReuYno8V4U0TWumfg/OwBXlbymcgYh
vIftzCUeJop8i+txfdUjv4V2D8Imvm/pdDZkM8esn89fTdFVU3QEw8eW/8YQ
d5W5ZEGV8VinWyDK9sSMYpsYDqbNWVYQERDJVscmHP1+AVKh61/lsWM5kFOz
J3G2QpoUd/OqYIv1T6e0Ascw+n1R4AdykBF2BCLZsUDZYYf28HK23tVljurk
dD1f37++74ll+UFVZ77txQHBqqtjY6Pkfv/+k8tg0O3puIxM05AHXJvrdIcD
yfJjVCZEcD4mLQqUjhEalsL9kwRopFbfGttDcNLC7suKqSmGqhgBce0oTXQW
2iL76ofRl6AfDBatn+m60QsS7tfI9YQ5ujMb9IXtf2Q9b0RVfE8b2WavJxJN
Vt0JRmFhQheUmpD0i9P1En1NhJiz6ZLw28fHYzqZhAh25FMHM7iIVkD+6AUD
ZT+/ZBKbI/yDXPdplbiWIQ97XEcQuQ4nqqZLHpFwh4ZSYAnzIlmF8j/X+j5G
epjhu7DZvIhmTl3dN2VVQtqXvKlrhy5EFaGvryCU7DhThJkuTS8dq1jYLHM6
pi6RcUVVCC1BxvWjGWv4yspdF7M0cCP4EsdstQbD4ViSVdNJIAPYEErXrzYE
eAGk6Tc6/Ts6k+91hvlxcezTyh1MtnX9pCLj+vwK6sS+APvP1kDr3+TkAYRB
tzMQWzft21ZXhLiZZhtM44qOtGUHs6ZE4ceVcTdX/8ISFYct3VPPdCpPhpSD
Q9fdjWB68JMazC0FFabeDJF2Zt6blr79el6ti8SSdVBAxU7q4xPrEW847GZV
Fmlo6yNhwOmO2G53B8QTEbifIiyRx74XeCVSRNtqgslQi3W9rtKHn5/3s/m1
tcylL2B7tuPYqOM4nB9fCAQy8NRAgB9NIm+dm5AE5rr9Trt9c3vLDQRRMTEn
U5LogYpqu15E0OipOUGfjeF7Z6DjhEwGnWPTyMpMtwm1WkT/UNYXhBjb4qaF
oyPEH1ZMS+wD6c2GpC9n6dSSROSJ6fFKXELH+60R0iPXQDw9sLVRf9Bv37Ru
2x2ux2DyeARGC4lA25m+P5yO+8wk+0K8CsP8VqvHj01Z7nIynDggtHSPvK+j
GOAjB+Y7L82cABYvpJ3ABEUdzL3b4Vp9sXPb6ZG1HdMl1unyj2VNkZHEQpDs
/umFBV9YpJXsHuSRVwuisR4klENgnCihE8AEBwtC8fk0nxLwtyzTYkWOaO4H
XEaMZkPg15KILxFp5nl+7BPBo/d7foJnXM4gBGepox4v8O0b+gftH6ZbL5Bp
I1rronM6Ro2NakG6mF5jXqA7b0cEsKrm6RTV5XEURARjLFVSnEmBcfJHNP69
Xd6/RmvTSZvH6lAeCzzf63Dgw6MRsqOs2VqDxpdqufF0mqES6vz0HZ6X5ege
7mGiaBMDWrehaTY9Cpo1FihXQU6U7Ps0iQOLUJjtZl8Trb+c+2o+9Q3UISFx
yHcHZlNqRdD3gKMRkQGSxR4nyzgAN53bFseL0lgQxRDWiayGaZuKLMI8EXVI
qjKvMQilLBabTV0VxTRDyNmzdeIdpq5KI82NiV0uWO/j8/emp5UtIXUxKqg/
EPgu1+mhdoP+JJJ6uqmRRVd1MmUY6ZWWKzpC53tIk7BBK9tVVUw8y9RMQ1fd
MEK1X56CcJVE8+4OGNVeZi5weDHfnJ+ZQhvr6KWvTrzQllm6tCcMep322J0U
i/WWyA/91WnoGsqo32nxkirw3O1tq0UXgO8LAi9FoUMHCsJ+SLyjcFnR3GKS
zKpqudvUm121OqwqOkEhIzaYgyMpij7uDRXIv+aQawQFBwffb+oy8WUUwgt8
H/k7YTTsi0hLQkYIKm8mdD69lO5TNCX3u96g/IRcLxr7ZmnsqLghdE7I1uqe
G4I0pGx4/SOB4rJMiOJEkZ/R7b4q1LEg1Z6239PFPsqmBj2u3W7zihOnM9Zp
ym7+WOjefvu705OHHJM+6nS5dqfTF9UkThx6O9WAjrNE+NJUVXI6tDub493h
eDwfTsdqt0VtFQSUFEnVxl2uzwaGoNspRBC5RgiqXlZ0zxy65AR/JAEfmBWG
KVD2tLBsW6OvYBuWl6C6Jkr3s4xecbEk54sUXRoZsgRNaWko+3Ywz5J4mqeT
eVNWBFiaxYnnkHkmeHdmirjXEOVmkYXmiB+I4mAAea/bm289yUSIBGlCh9wx
3/r27a9vN51en4f8GR0Snj5BR9D+D94JPnc=
"], {{0, 1675.6363636363637`}, {
1675.6363636363637`, 0}}, {0, 255},
ColorFunction->GrayLevel,
ImageResolution->{11, 11}],
BoxForm`ImageTag[
"Byte", ColorSpace -> "Grayscale", Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1675.6363636363637`, 1675.6363636363637`},
PlotRange->{{0, 1675.6363636363637`}, {0, 1675.6363636363637`}}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/65611dbe4b6eae6e.png)
|
| Out[3]= |

|
Apply the normal texture to a polygon (MaterialShading requires Wolfram Language 12.3):
| In[4]:= |
![Graphics3D[{MaterialShading[<|"SurfaceNormals" -> Texture[%]|>], Polygon[{{1, -1, 0}, {1, 1, 0}, {-1, 1, 0}, {-1, -1, 0}}]}, Boxed -> False, ViewPoint -> Above, Lighting -> "Accent"]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/188eab18fdbd459d.png)
|
| Out[4]= |

|
Use elevation data of real world locations:
| In[5]:= |
![elevations = GeoElevationData[Entity["Mountain", "MountEverest"], GeoRange -> Quantity[10, "Kilometers"]];
ResourceFunction["NormalTexture"][elevations] // Image](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/3678be6e9bd24d28.png)
|
| Out[5]= |

|
Use textures:
| In[6]:= |
|
| Out[6]= |

|
| In[7]:= |
|
| Out[7]= |

|
Use graphics:
| In[8]:= |
|
| Out[8]= |

|
| In[9]:= |
|
| Out[9]= |

|
Create normal textures with varying strengths:
| In[10]:= |
![ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztmgtM1VUcx6HymfEQxygzvS4fgM4Jci/85Z6DxmyIgo+wkqxIhZyPUFNg
ive6LFRCVJgamI9JBoIvVCRuQmkZPtq0sCajGJSPzFYuFa9t2PlcuZtjyrCw
xn+e7bjjOb/f9/s9//85v/M7/4vhjbcmxD/i4uIyv7P6Z0Jc0oh58+JSJnbk
P9PjZgUGzGIwoKk+LPotOUElAeeTBwV207rvT0p1NUVmZpmWNZQ6Km36GMMG
2/9br7PkB/ULGDdheNAm++/Dfug/xJR9Sgvpa/PRuvsv16om52teIw9o9pJP
HZU2fYxhgy0++IIB1n+t//KqXYGb/3zB+KvXRyVjHk0PbpzrpxmO7dAiCsO1
l1OXl/WyjbItrU6zVVaut62v2OKotOljDBts8cEXDLDABPtB6/9KjguI8Yk2
Lj7hW1I3KcFUc2Wk9kt8lrZv18GyDLdVttO73Wz+9trhHcbmhXZb29VcPNNo
7vRdpKPSpo8xbLDFB18wwAITbDjgehBzOLtt2zBDrydNlw5FlT5l2hcyxCdX
O51wuWxa4kKbPdkztH5yL/Peglyza9058/RaT5Hn6SvWpQQLy/AwR6VNH2PY
YIsPvmCABSbYcMAFZ1vOodY9P2jV8jrjiO5bS9/v8ro2dtl7B3vGLbHN9gwO
ze053ezqd8FctNFXjPprkrj62mJRKDPEyeINonzGFhEXkeeotOljDBts8cEX
DLDABBsOuOCEuy3mEPLj9aAjmW4HyhfGlX5StU6zf2EvS+gfqxXGDDXvjLxo
3t4vRIzY+bbwPZwtVnoXiWMNFeL73qdE4LQaUZD3syg8ftFRadPHGDbY4oMv
GGCBCTYccMEJNxr+7XsoVzg9UrxKtw36UDu2I9wW//jA0EVrNpqvnekrEj1n
i/wVG8S8GwfFkcAq0efaZZHg6ior1naR27095E8pPeTNXd6OSps+xrDBFh98
wQALTLDhgAtOuNHwT99LtVqbGeq98kzAyxgfY/v8Ynqo1wfHzQNqwsR4/xUi
57E9Yu6wKmGMuSauKH2G3d5yX41BFjf4ybKaoTI5xSgbjwc7Km36GMMGW3zw
BQMsMMGGAy444UYDWqrvc78cVbGCfcYa5f1WqmcD7pGoanPSymgRtTFblN+o
ENdPXBSpMzvJ5PM+MnrPQNkh0yhl+Ei59bdI6Zo1UXpcekmu3RzrqLTpYwwb
bPHBFwywwAQbDrjghBsNaEHT0fuIY8Q9Ygb77Sb7Qb1nnhH4y5M3iJKOlSJb
PccTap24G56V1TlGebj38zLHfZL0Lpoq37HOkVNyF8ioxBQZG77IUWnTxxg2
2OKDLxhggQk2HHDBCTca0IImtLVmDpxDqSqGE/+eU7GDfcea5X3zrOBJTbeL
k2q9D2/0k3PcwmTR7IlyiSle1h1aIHs8s0R+OcMqG9dYpf98q1z96u1Kmz7G
sMEWH3zBAAtMsOGAC0640YAWNKGtNWclZ2q9Oo+I5U+rOEgMYf+xdnnvPDP4
9o4dLD3OhEv7gFh54Y9E2e/NJbIo3SqTDFaZXWaRqz+2yDEHLDK2/HalTR9j
2GCLD75ggAUm2HDABSfcaEALmtCGxpbmUKBynEsqP+Bs/UadS8R04iGxhH3I
Gub9a+rZwVt/coocfHKBfHGqVQb3scqlmyzyibMWOc1ukRG3LLJW1atNlTZ9
jGGDLT74ggEWmGDDAReccKMBLWhCGxoLWsjHolW+Rq5DnjBVnbE56nwithMX
iSmL1X5kLbMOeIbwd0izSvfPLPL8cYsMc7XKr5XWelVdXKx3rYxhgy0++IIB
FphgwwEXnHCjAS1oQhsa0XqveWxRuectlbftVzkP+QJnLecUMZ74SGxhX7Km
WQ88Sw+l41KdRe5WutKUvlstzMFZscEWH3zBAAtMsOGAC0640YAWNKENjWi9
1zzIo8lByd/Ifcgb/NSZy3lFrCdOEmPYn6xt1gXPFD15rdDfvOY1zQUMsMAE
Gw644IQbDWhBE9rQiNa7zYF7DXeC0Sqf/lblosUqjyMHIn/g7OXcIuYTL4k1
7FPWeFjTe7jfOThrWtMaAwtMsOGAC0640YAWNKENjWi9213snLqjGdT9hruB
n8qrXVROSj5HLkQewRnM+UXsJ24Sc7qdvb3WW7OWWlpjYIAFJthwwAUn3GhA
C5rQhka0orn5PLqq+yZ3Ne453BHIr8lNyevIicgnOIs5xzgDiJ/T7S3v6dZW
MMACE2w44IITbjSgBU1oQyNa0dx8Hsnq7sy9kzsb9x3uCuTZ5Kjkd+RG5BWv
qDOZ84yzIKIN5uCsYIEJNhxwwQk3GtCCJrShEa1obj6P0ZlZJu7Q3D/3qrsb
9x7uDOTb5KrkeeRI5BeczZxrtW04D7DABBsOuOCEGw1oQRPa0IhWNDefx7sN
pSa+B3CX7qzuodzhuP9wdyDvJmddo/I9ciXyDM7oq204D7DAdGArDrjghBsN
aEET2tCIVjTrdR56WVd62ed6ibt6OQf1kpdQ9JAnUvSSt+vlHqWXey1FD98Z
KHr57kPRw3c4il6+i1L08J3aWfTwu4Gz6OF3nDvfS3v/Xc1Z9PA7p7Po4Xfn
O0t7/zuA5qW9/13GvUp7/TuZh6Xty98hpCH+
"], {{0, 50.}, {50., 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{50., 50.},
PlotRange->{{0, 50.}, {0, 50.}}]\), #] & /@ {1/2, 2, 8}](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/4c7d6e7652256094.png)
|
| Out[10]= |

|
Use different vertical and horizontal strengths:
| In[11]:= |
![ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztnQtUVdXWx0GNfAESFFoGko985JsDHGCvGWmYj0J8paYG+OyaplkhPjjo
1fpKMR+JZqaiVy2jz8wHetRItERUvF4kDJHKIG9qklqaD/Dbv42OcccdjUYl
yu4be42xcrf3WnP+//99zt5rrTnXISDuhV4jqrm4uEyoqf+nV2x8xIsvxib0
duN/hsc+37HD81wcdqNaxSpWsYpVrGIVq1jFKlaxilVcXC7GDLd9OrzzlgNl
Xwfn7j0c8lNwO3v6urX2tQfK7edKGoW26xsa2jS6e2jHw72NyjHnuEYb2tKH
vtjAFjarmtdfpWi9fW0/zlq8+dFIj+AZkXtCAvzn2mdcbBwaEN8xdN6oDPuU
kiUhmX19nbkd33ee9jvnLCr03u5Rv9n2guC2RuWYc1yjDW3pQ19sGLawqdvG
B77wWdW8zVTGvbEgsHuGn+3x042D4pPfDPmi/wb78/FBoX4dsu2bVuVtO9D+
sjNxUr3tk0ZMd57/oId90fS5YV/Wrh9+/sc+4WNTp4XPrD8vvDRvsVE55hzX
aENb+tAXG9jCJrbxgS984hsMYKlqPaqqdHYLtq05tizQVtwkqMYhH/sMh3fo
N1Ju3xoX5Fx5zXN7j3tWOJ9dMSzs+9pR4WNGfhpeWs9Xq+7bRTsQNUH7Yvds
rWv1pVrC1LXamw+v194q+9ioHHOOa7ShLX3oiw1sYRPb+MAXPvENBrCACWxV
rc+dKgNONLftOrnc1nZVwpYn32lin7SpcWjraQ/Yn8jNdX5SL8fZOWZZmPvq
BeG5Afdpbrbh2lMrF2uLopzalob52jvxP2pLLlVTzxfVUZfv8lbJI+qr78oe
UJ7ZDxqVY85xjTa0pQ99sYEtbGIbH/jCJ77BABYwgQ2MYK1qvW5X2TzPI7D1
Rz2DfhjVOj0he1vIvjTf0L97ZYYs9i9z9v+lKCRtdJfwyc1ratffHqOtqPOe
Nn9trjbO76oWEuup5iz1V/c83kbZW4SpqV0i1e6UKPWS59Nq14eD1MixMerx
qDijcsw5rtGGtvShLzawhU1s4wNf+MQ3GMACJrCBEaxgBntV61eZ5cS/d9nq
T8gPXLYyMD32+wL7hnmf21+697jT9e4V9rWzJofPer2V9lbaPG3l1SwtofyK
1j/dR/ktaqnu/lqpSROj1erecerwyPFqR1qiesl9pirOe119lZasHpo7V12Y
Ol81e3mBUTnmHNdoQ1v60Bcb2MImtvGBL3ziGwxgARPYwAhWMIMdDlWtY2WU
DXOWBJ16ZWP61IS8kOqrW4dqbhOcWT+87Lw8ok94gwOtNG3m29qHT+drV/xr
Kv9HG6vqtTSlQvqqmrtGq3e7J6lv8l9XXknzVVdZoty9UlX0uTVqZuEH6t1D
61XTrI9V6J5NKiVzs1E55hzXaENb+tAXG9jCJrbxgS984hsMYAET2MAIVjCD
HQ5wqWo9/2z5+5NNbTNyZwX1dG28NTV5p332B5/ZV8aXOZPidoSJa02t+/w5
2qeZuZqzsJZKzmiujkZHqq8HxKmyA1NUac4bKvvZFHX8nlTV4cQ61SRroxqV
sV09tDtTncrJUsVFB9Wu0sMqp/yIKq+Vr855HjUqx5zjGm1oSx/6YgNb2MQ2
PvCFT3yDASxgAhsYwQpmsMMBLnCCW1Xr+0fKwsfm2NrmewaOfaraVhfNJ3Rw
yn3O+3c+64y+e374awUx2u5xn2iLPqimjns3VdX6RKo6/iPUOtt01WLhXFXQ
bJna+u069e2eLWrD7l1q45f71UGXPBXZ8bjKG12sNqw+pVILS1Ud959UWcdL
KjjqsrINvmJUjjnHNdrQlj70xQa2sIltfOALn/gGA1jABDYwghXMYIcDXOAE
NzhWtc6/p3Rvctj22vJXtmiuP2+e3rpV6HXXuc6fw5qFfR7sol1bkKJdH1Ci
ZXSurxZ5aOrslBh19LFpyiN5nnrx3lQ19sh6NTZzp7qQn60WueerloNOqJ07
zqj/bX5R7X+7XDW/q7pMD3WTNadqylLvOvL5xrpyap+7tOvrYVSOOcc12tCW
PvTFBrawiW184Auf+AYDWMAENjCCFcxghwNc4AQ3OMK1qvX+rfLmI65B2wpq
pUccyQ8uqxcW2i32rPOx3qVhCYcDNcneqC1bUk1dTGmp+syIVksD4tXqjcnK
8dByNTpvvRq+J0MNPJmj2gcdV0XvnVLjgy8p7zGusnOPmzRaXkcKf/GU/Tne
cp+fr9iKG0iZX0NJO/CgfHvaT7ZN9jcqx5zjGm1oSx/6YgNb2MQ2PvCFT3yD
ASxgAhsYwQpmsMMBLnCCGxzhCueq1v3XCp8Vp47vjfc8QzIKO4Q+e6Ha9ri9
bcIXzh6oVau7TzvZylONHWRXXWPiVILPTFXee7Fa9d06/R28Q8UUH1RvqyLV
JfsHtTvxmtrc4i45quu39F0vOaNrWuzfUHKXNpLu85tIm7KHZXNBS3E0by2L
ituIw72d2FZWVI6Nc/o12tCWPvTFBrawiW184Auf+AYDWMAENjCCFcxghwNc
4AQ3OMIVzmb7nqToz9LX9e8vnxlwvjP0rPNCh/7hRx4drxWG5WuJj9ZXe6d0
Vt/Me0Gt/WS2WuSbqt7dv0kN+ddeFda4QD2z+bTa6rim5oe7SfsD7nLfKR9Z
Pe8B6f9JgOwZ/bC8v/ARcQ1pL7WjbNIvP0SOHgyTH9oqGXtVZHObCFmRVVE5
5hzXaENb+tAXG9jCJrbxgS984hsMYAET2MAIVjCDHQ5wgRPc4AhXOMM9xSTv
E8YaLfT3W7D+TOV7PET/7JzX8QbVTdByIoq0N7Y9qN472139rVaCint1vrp0
Ya16+rMdyuv8P9WI8cWqU+gltTa1hkyJcBdn/L0yQR6U9xc0kVEvtJLPDraX
n98Plv7Xw2X6vgjpVyNSaqd1lYidPcTLFiX3ekVLQlQvuXK2onLMOa7Rhrb0
oS82sIVNbOMDX/jENxjAAiawgRGsYAY7HOACJ7jBEa5whjsamGHcNVMf/zHm
mKa/57rqz1a+z3n6Zwjcpcn+Kub9KFW2PVFlDUtRm75OU7v2ZarZvkfVE7vO
qJIhLrLXtbYM6OwtrwU0FP+3msiRlEfkqSaB0jE4TFpnR8jdR7vI/GeelJ09
e0nkh/3k4piBcm7uYNl5T4wcuxgraaFD5UxhReWYc1yjDW3pQ19sYAub2MYH
vvCJbzCABUxgAyNYwQx2OMAFTnCDI1zhDHc0QIuqvBfMjxiTMw5k7MH7jmcs
32s+S+CfGJ2kWvZdrNbmr1cPHv5cRduPqzfuvqB6N6gh/9PfQ4aG15ePMwLk
nuMt5fKcjvLJoTBZ9XYn2fZdNynfEC37fnxaui4eLGuWxcnqtiPlyc6jJTpj
rHRYMV48sifIxfCXpeBiReWYc1yjDW3pQ19sYAub2MYHvvCJbzCABUxgAyNY
wQx2OMAFTnCDI1zhDHc0QIuqmjOyfsCcdaU+Txqij80ZDzIG4b3Hs5bvN58p
eHjmfaSafJGlnuv5tRoadknV2usmU5Z7icdDDSWxazPpU6+dFI6zS8fhj0nD
k90k9lwvaTBxoLw7NFamHR0pW66NkWN7JsjCQROlw/HJstInUd5ydcj2LIe8
1jRJmkVWVI45xzXa0JY+9MUGtrCJbXzgC5/4BgNYwAQ2MIIVzGCHA1zgBDc4
whXOcEcDtECTO722wvra/RPyA1lHYO7qq8+XGKMzLmQswvuPZy7fcz5b8Enp
/4060u+y8h5WU9Yc9paQUj9ZlN5CujQNlFc7KGn3ZRdJ8I4Wn4IBUrNunHz1
r+dkzmvjZdHQiTK011S5tNUhE3skSY/wJGnfJknivZPkdZckGXzSIQkFFZVj
znGNNrSlD32xgS1sYhsf+MInvsEAFjCBDYxgBTPY4QAXOMENjnCFM9zRAC3Q
BG3u5Boka56ss7G2w3pCL30Oy7yJsTrjwxP6mIT3IM9eP/37zmcMXm5na8ri
0z4yeHkj6VTjESnxCZbZ+yPknwE9JMinn4yd9awUTRol78WPlzUfJkjb/Yni
q2vaOTBJBlZPkrw8h2w45pC7vnFI3hmH+P/skMwrDkkpq6gcc45rtKEtfeiL
DWxhE9v4wBc+8Q0GsIAJbGAEK5jBDge4wAlucIQrnOGOBmiBJmiDRnfiXhAT
YB067vsCu7hNMNajXi2IMebdl/T5Uzd9zM448aI+NsnU34c99Wcw33s+a/Db
1jZAFrdqLeVfhkhXW2eZGBwl3Y4PkA+vDJV/FI2Rx3bHy5kZiVLWKUnW1U+S
2rqmm4oc8vBPDll43SFD9FpD/w6U6/+66P/+Wi2/0Ya29KEvNrCFTWzjA1/4
xDcYwAImsIHRwKpjBjsc4AInuMERrnCGOxoYa3O6JmiDRncifpJ5crltUva2
ENajs3942cm6G2s9rC8wp2Uexdi9nz5eZIzCe7Gm/izm+2985nSew8bbJWr0
4+LpEy0/Dx8ke/R37taHXhQpnyzXWiTJcv8kKdA/1+XfOyS93CE/6Zqe1+tv
3YPfujf0xQa2sIltfOALn/gGA1jABDYwghXMYIcDXOAENzjCFc5wRwO0QBO0
QSO0up33gjhmu1UJW7LSfEOJEbAuzVoo62+s+bDOwNx2mT6fYgzPuJGxylT9
/cgzmecAn72ndL5Pb4wWx7rB0rbZc5Jc8pJseCpRntCf9XX1z3FKiUMa6FpW
12upruP1P3Ef/rtiA1vYxDY+8IVPfIMBLGACGxjBCmawwwEucIIbHOEKZ7ij
AVqgCdqgEVrdztgvsWXimdO8MkOI2xArYH2aNVHW4dZsTDbWG5jjMq9iLM/4
kTEL70mezTwP+AzCe8iB5+R8v1dkjM0hzVsmiXeOQ7KvOmScrldWJd2HX7sv
2MYHvvCJbzCABUxgAyNYwQx2OMAFTnCDI1zhDHc0QAs0QRs0Qis0ux33gtyL
wOImQcSYiWuumTU5nPjN9sJaqnqfSGNtlPU41oBYd2Cuy/yKMT3jSMYuvC95
RvNc4LMI/4HTHPL5/UnS+KiujWuS5OpaXb0N9+G/Kz7whU98gwEsYAIbGMEK
ZrDDAS5wghsc4QpnuKMBWqAJ2qARWqHZ7chb6ZHhZ6t+yMfedtoD9ua/FIUQ
3ySmRhyH2AHr1ayRxhYfNNaCWH9gzss8i7E940nGMLw3eVbzfOAziQ5N9fds
lK7Lp7o+ZXfgXtys+MInvsEAFjCBDYxgBTPY4QAXOMENjnCFM9zRAC3QBG3Q
CK3QDO0q+350Pt04iLwYcjGI/xNzJs5JbI14DjEE1q1ZK2V9bnKEu7EO4aXP
fZlvMcZnXMlYJl1/f36sP7N5TvDZ7Knrse1Pvq9vteIT3z1vfE/ABDYwghXM
YIcDXOAENzjCFc5wRwO0QBO0QSO0QjO0q8x7oXr72l5JfjPkhJTbM+rlOMnJ
IA+A2DPxTmJsxHWeOZljrF+zZso6HWtDrEcE6nNg5l2M9RlfKn1M07VHxfvC
+8b3oiruxX/ek09vPLvABDYwghXMYIcDXOAENzjCFc5wRwO0QBO0QSO0QjO0
U5WYB3lu1uLN5PJtiQtydopZFuayZIyRB0I+ADFo4p7E2ojvZCZeU6xjs3bK
el3GoTBjXYK58Ff6/IsxP+PMOkUV7+7cO/yM+q1nF1jABDYwghXMYIcDXOAE
NzgaXHXOcEcDtEATtEEjtEIztEPDyrofEZEeweRXktNHHhm5S+TLSEhfIy+A
WDTxT2JuxHmILbCezRoq63Yx53pJrbpxxpyYeRhj/4UlFWOcO/Hu/r316o1x
F9jACFYwgx0OcIET3OAIVzjDHQ3QAk3QBo3QCs3QDg0r636Qf0zOK3mWRwLu
M/LJyGGqtWu0katBfgAx6XHBlxSxN+I9xBhY13Z+181Yv2PNiHUK5sbMx5gD
ZJnoXtysYAIbGMEKZrDDAS5wghsc4QpnuKMBWqAJ2qARWqEZ2qFhZdwL8vPJ
CU9flbctdsWwMPItyfEjr4xcJvJnPtq9S7UadMKIdxMPJQZH3IdYA+vbrKmy
jtduf2LFesX3FfOy2zG/uNV6/cacEYxgBTPY4QAXOMENjnCFM9zRAC3QBG3Q
CK3QDO3QsDL2OrBngjx9csPJRyYH1h7raeT6kV9GThN5NORu7NjjZsSoiYsS
iyP+Q8yBdW7WVlnPq3OsYt2i1IT34mYtvbG2AlYwgx0OcIET3OAIVzjDHQ3Q
Ak3QBo3QCs3QDg3R8lbvB/tY2DtBvj454uQlv7nUX/2jd5yR80eeGblN65tf
VORwkDdArJr4KDE54kDEHuJ6TZVOgUnGut5Pt2nuXZnfETCCFcxghwNc4AQ3
OMIVznBHA7RAE7RBI7RCM7RDQ7S81fvB3qIFozLsk0dMd5K3n94wXyM/mZzY
brJEjczYbuSbkeN07BdPI5eD/AFi1sRJic0RDyIGwbo3a63nTXwvbtbzN9aF
wQx2OMAFTnCDI1zhDHc0QAs0QRs0Qis0Qzs0RMtbvR/s9xpfsiTEPa2HvZpv
FyPnn5zxnWmJysMr1cjHJAeQvLMDOd5Gfo2RB1Ij0ohdEy9NGTTRiAsRi1hY
xXON31vLb6zVgxnscIALnIy8Cp0jXOEMdzRACzRBGzRCKzRDOzREy1u9H+zB
Y98Xe43Y38KeCvL4yR0nX/l0TpaRl0kuIPln5DwZeTZpXY18AmLYxE2f1J/D
xIeG/AXuxc0KVjCD3eCgc4GTkbeic4QrnOGOBmiBJmiDRmiFZmiHhmh5q/eD
fZHsxWP/F3uO2OeSmRJl5POTQ07e8srCUkV+ZmBxAyMPjdynR3f2MHI8yCtI
9Uk04qfE7GqYQOffW8EKZrDDAS5wghsc4QpnuKMBWhia6NqgEVqhGdqhIVre
6v34saRR6Bm/c0725LEPjL1H7Hdhj8WyQ+uNXHLyl8mZLfdraOQGko9GDhR5
N+R6kF8w0TvJiKP+FZ5V//nMAjPY4QAXOMENjnCFM9zRAC3QBG3QCK3QDO3Q
EC1v9X6wf5g9q+yTnDR1rcZ+MPYgse+FvRbk91/reEnt3VjXyJ0lX5McQfLS
yIVyz55g5HyQZ0Bsu6o1/qMVzGCHA1zgBDc4whXOcEcDtEATtEEjtEIztEND
tLzV+8GebvYRs3eV/ZLs0Rs1NsbYi8T+l+u18lVQ1GVFbvmJ035GDi15m+QK
kp92KfxlIw9nyMmKfIOq1vePVjCDHQ5wgRPc4AhXOMMdDdACTdAGjdAKzdAO
DdHyVu8H++zZ281+Yvawsm+SvXrsD2NPEvtg2HtBvj855uQ1p2ZFGPmb5AyS
p/ZwZJKRj0MOSFXr+0crmMEOB7jACW5whCuc4Y4GaIEmaINGaIVmaIeGaGnd
j/9f98N6XpnreWW9z831PrfGu+Ya71rzQXPNB631EnOtl1jrieZaT7TW2821
3m7Fo8wVj7LiteaK11r5DObKZ6BY+T7myfehWPlw5sqHs/JFzZUvauVTmyuf
mmLtNzDPfgOKtR/HXPtxrP1q5tqvRrH2c5pnPyfF2u9srv3OFOv3AMzzewAU
6/cyzPV7GRTr92TM83syFOv3lsz1e0sU6/fIzPN7ZDeL9Xt95vm9vpvF+j1L
8/yeJcX6vVdz/d4rxfo9ZPP8HvLNYv1euPmK9Xv65ivW35swX7H+Hov5ivX3
isxZrL/nZb5i/b078xXr70Gas1h/L9Wcxfp7wuYs1t/bNm+x/h69uQv5+eyZ
YB8Le4vY78UePPZFnitpFMr+YfZ0s8+eyjHnuEYb2tKHvtjAVmXl/FvFKlax
ilWsYhWrWMUqVrHKX738H0hGOzM=
"], {{0, 100.}, {100., 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{100., 100.},
PlotRange->{{0, 100.}, {0, 100.}}]\), {2, 8}]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/7c245c9b5a4d8301.png)
|
| Out[11]= |

|
Negative strength values reverse the normal direction:
| In[12]:= |
![ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztmgtM1VUcx6HymfEQxygzvS4fgM4Jci/85Z6DxmyIgo+wkqxIhZyPUFNg
ive6LFRCVJgamI9JBoIvVCRuQmkZPtq0sCajGJSPzFYuFa9t2PlcuZtjyrCw
xn+e7bjjOb/f9/s9//85v/M7/4vhjbcmxD/i4uIyv7P6Z0Jc0oh58+JSJnbk
P9PjZgUGzGIwoKk+LPotOUElAeeTBwV207rvT0p1NUVmZpmWNZQ6Km36GMMG
2/9br7PkB/ULGDdheNAm++/Dfug/xJR9Sgvpa/PRuvsv16om52teIw9o9pJP
HZU2fYxhgy0++IIB1n+t//KqXYGb/3zB+KvXRyVjHk0PbpzrpxmO7dAiCsO1
l1OXl/WyjbItrU6zVVaut62v2OKotOljDBts8cEXDLDABPtB6/9KjguI8Yk2
Lj7hW1I3KcFUc2Wk9kt8lrZv18GyDLdVttO73Wz+9trhHcbmhXZb29VcPNNo
7vRdpKPSpo8xbLDFB18wwAITbDjgehBzOLtt2zBDrydNlw5FlT5l2hcyxCdX
O51wuWxa4kKbPdkztH5yL/Peglyza9058/RaT5Hn6SvWpQQLy/AwR6VNH2PY
YIsPvmCABSbYcMAFZ1vOodY9P2jV8jrjiO5bS9/v8ro2dtl7B3vGLbHN9gwO
ze053ezqd8FctNFXjPprkrj62mJRKDPEyeINonzGFhEXkeeotOljDBts8cEX
DLDABBsOuOCEuy3mEPLj9aAjmW4HyhfGlX5StU6zf2EvS+gfqxXGDDXvjLxo
3t4vRIzY+bbwPZwtVnoXiWMNFeL73qdE4LQaUZD3syg8ftFRadPHGDbY4oMv
GGCBCTYccMEJNxr+7XsoVzg9UrxKtw36UDu2I9wW//jA0EVrNpqvnekrEj1n
i/wVG8S8GwfFkcAq0efaZZHg6ior1naR27095E8pPeTNXd6OSps+xrDBFh98
wQALTLDhgAtOuNHwT99LtVqbGeq98kzAyxgfY/v8Ynqo1wfHzQNqwsR4/xUi
57E9Yu6wKmGMuSauKH2G3d5yX41BFjf4ybKaoTI5xSgbjwc7Km36GMMGW3zw
BQMsMMGGAy444UYDWqrvc78cVbGCfcYa5f1WqmcD7pGoanPSymgRtTFblN+o
ENdPXBSpMzvJ5PM+MnrPQNkh0yhl+Ei59bdI6Zo1UXpcekmu3RzrqLTpYwwb
bPHBFwywwAQbDrjghBsNaEHT0fuIY8Q9Ygb77Sb7Qb1nnhH4y5M3iJKOlSJb
PccTap24G56V1TlGebj38zLHfZL0Lpoq37HOkVNyF8ioxBQZG77IUWnTxxg2
2OKDLxhggQk2HHDBCTca0IImtLVmDpxDqSqGE/+eU7GDfcea5X3zrOBJTbeL
k2q9D2/0k3PcwmTR7IlyiSle1h1aIHs8s0R+OcMqG9dYpf98q1z96u1Kmz7G
sMEWH3zBAAtMsOGAC0640YAWNKGtNWclZ2q9Oo+I5U+rOEgMYf+xdnnvPDP4
9o4dLD3OhEv7gFh54Y9E2e/NJbIo3SqTDFaZXWaRqz+2yDEHLDK2/HalTR9j
2GCLD75ggAUm2HDABSfcaEALmtCGxpbmUKBynEsqP+Bs/UadS8R04iGxhH3I
Gub9a+rZwVt/coocfHKBfHGqVQb3scqlmyzyibMWOc1ukRG3LLJW1atNlTZ9
jGGDLT74ggEWmGDDAReccKMBLWhCGxoLWsjHolW+Rq5DnjBVnbE56nwithMX
iSmL1X5kLbMOeIbwd0izSvfPLPL8cYsMc7XKr5XWelVdXKx3rYxhgy0++IIB
FphgwwEXnHCjAS1oQhsa0XqveWxRuectlbftVzkP+QJnLecUMZ74SGxhX7Km
WQ88Sw+l41KdRe5WutKUvlstzMFZscEWH3zBAAtMsOGAC0640YAWNKENjWi9
1zzIo8lByd/Ifcgb/NSZy3lFrCdOEmPYn6xt1gXPFD15rdDfvOY1zQUMsMAE
Gw644IQbDWhBE9rQiNa7zYF7DXeC0Sqf/lblosUqjyMHIn/g7OXcIuYTL4k1
7FPWeFjTe7jfOThrWtMaAwtMsOGAC0640YAWNKENjWi9213snLqjGdT9hruB
n8qrXVROSj5HLkQewRnM+UXsJ24Sc7qdvb3WW7OWWlpjYIAFJthwwAUn3GhA
C5rQhka0orn5PLqq+yZ3Ne453BHIr8lNyevIicgnOIs5xzgDiJ/T7S3v6dZW
MMACE2w44IITbjSgBU1oQyNa0dx8Hsnq7sy9kzsb9x3uCuTZ5Kjkd+RG5BWv
qDOZ84yzIKIN5uCsYIEJNhxwwQk3GtCCJrShEa1obj6P0ZlZJu7Q3D/3qrsb
9x7uDOTb5KrkeeRI5BeczZxrtW04D7DABBsOuOCEGw1oQRPa0IhWNDefx7sN
pSa+B3CX7qzuodzhuP9wdyDvJmddo/I9ciXyDM7oq204D7DAdGArDrjghBsN
aEET2tCIVjTrdR56WVd62ed6ibt6OQf1kpdQ9JAnUvSSt+vlHqWXey1FD98Z
KHr57kPRw3c4il6+i1L08J3aWfTwu4Gz6OF3nDvfS3v/Xc1Z9PA7p7Po4Xfn
O0t7/zuA5qW9/13GvUp7/TuZh6Xty98hpCH+
"], {{0, 50.}, {50., 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{50., 50.},
PlotRange->{{0, 50.}, {0, 50.}}]\), #] & /@ {2, -2}](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/07417e3ee7dc87bf.png)
|
| Out[12]= |

|
Create normal textures using increasing radii:
| In[13]:= |
![ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzt0bGpAlEARNHFQGzDFkRMxRa0ghU0EgQNxK4tQQWTyQw+DH7OgX2P5WV3
5vvz9jgZhuE6ex3b8ba5XMb7bvr+OYyn1fLwflx8PgAAAAAA+N5j/Vv3f9fu
a4/U7muP1O5rj9Tua4/U7muP1O5rj9Tua4/U7muP1O5rj9Tua4/U7muP1O5r
j9Tua4/U7muP1O5rj9Tua4/U7muP1O5rj9Tua4/U7muP1O5rDwAAAAAA/tYT
wZ1FXQ==
"], {{0, 50}, {50, 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{50, 50},
PlotRange->{{0, 50}, {0, 50}}]\), 1, #] & /@ {1, 10, 20}](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/522ea9739559af3d.png)
|
| Out[13]= |

|
Use different vertical and horizontal radii:
| In[14]:= |
![ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzt0bGpAlEARNHFQGzDFkRMxRa0ghU0EgQNxK4tQQWTyQw+DH7OgX2P5WV3
5vvz9jgZhuE6ex3b8ba5XMb7bvr+OYyn1fLwflx8PgAAAAAA+N5j/Vv3f9fu
a4/U7muP1O5rj9Tua4/U7muP1O5rj9Tua4/U7muP1O5rj9Tua4/U7muP1O5r
j9Tua4/U7muP1O5rj9Tua4/U7muP1O5rj9Tua4/U7muP1O5rDwAAAAAA/tYT
wZ1FXQ==
"], {{0, 50}, {50, 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{50, 50},
PlotRange->{{0, 50}, {0, 50}}]\), 1, {1, 10}]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/645a85592846d0c2.png)
|
| Out[14]= |

|
Compute the horizontal and vertical derivatives using the default Sobel method:
| In[15]:= |
|
| Out[15]= |

|
Use the Gaussian method:
| In[16]:= |
|
| Out[16]= |

|
Use custom kernels for computing the derivatives:
| In[17]:= |
![ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzt0MFpAlEYhdFHFsE20oIpQOwgaAUj6EoQzCJkl9KjYAcXHtzhfHAHHrP6
z8fpdri8jTG+N4/PYfnZ3+/L7/H9+Tgv18/t9fnz67Ux/nbzNquZN/HrGT9+
/HrHjx+/3vHjx693/Pjx6x0/fvx6x48fv97x48evd/z48evdGv1mtsabZsYv
i18Wvyx+Wfyy+GXxy+KXxS+LXxa/LH5Z/LL4ZfHL4pfFL4tfFr8sfln8svhl
8cvil7VGv1k3zbxr5k38esaPH7/e8ePHr3f8+PHrHT9+/HrHjx+/3vHjx693
/Pjx6x0/fvx6tz6/f6XjgS8=
"], {{0, 80.}, {80., 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSize->Magnification[0.5],
ImageSizeRaw->{80., 80.},
PlotRange->{{0, 80.}, {0, 80.}}]\), Method -> {({
{1, 0, -1},
{1, 0, -1},
{1, 0, -1}
}), ({
{-1, -1, -1},
{0, 0, 0},
{1, 1, 1}
})}]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/66b8ac7d8de38e2f.png)
|
| Out[17]= |

|
Compare different methods with increasing kernel radii:
| In[18]:= |
![methods = {"Sobel", "Gaussian", "ShenCastan"};
Grid[Transpose[Prepend[Table[ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztW3dUVEf7plgQLIBIs6KANGkLl91l74wFQwRUFFtiiaBBRQTFGo2CBVAU
QbEgiIoCNpC2sLCLINgVsCAKih072Asajb95Nl/O8eSXxCR+f5jvuOdMzs29
7/s87x1m3jZXE7/gof5qKioqMzXYf4b6zu0TEuL7g08L/M/3voECx0A89P7P
+NjvWHMrs0dpjZbLQgf0qspNtev/dFO2WYchgiGX1KS3dCc6NW/nwvkpCPfT
DT1uaWUL5cA17uEZZCALHegCA1jABPZfMOEPfz3Njbrv9whOW11TZNm+/KHN
0O0Ftp5j6jN3xwzJ2p/vL6gt/Fr6VVK21KJOkwuUref27SzmWlkd5ST1GdzA
7EncvA4mzhWOTdIC822OT+LKHZNPr86Obrxhd90kqldRXjtrY689FocHnTX9
J7Y1FjYz2zQi3sq4zTvrIfMaMgOOejgOVR2YW/K6v1O7yRJuRp5p/pGDMpcs
fR3RZO1i0eFXOuLYd5bKgWvcwzPIQBY60AUGsIAJbHCA6+/at/y7wT08K/Us
lqd3t9F56GiruaWrvfpPwxzf1rXLsdgZKdj2OIYrTuPyuzoOlY3wu+ASc2C5
8HRyjnD3OIVwbUiy8O19T+EAwwrnFi97y2JvzOSiv1bn1h2Oll4cP03Q6eeK
zGsqe+zK3knTBye6Wf6wu5l5hKS461+x66Ljom43T5al5eiq7tV8/cD29O3H
WYbHWwvaPnJwShTt4Qz62ciizlmIPFSdxdR5nvhyO3Xx64UPC0Mf75I3BtUp
B65xD88gA1noQBcYwAImsMEBLnCC+6/YaD9msXlbszN7PKe02Jc0cZP92tTv
HdLUknLuTt4sKPhmKbeD05OlNjoL+Rc7RZNOWIsHbTUUnzO7I0q5dlj09YZi
0a67VaK+Nmrigthe4tXXNMTyo4Yi6mzs7CjwzN/1fjo3sJtznmxzjcDNvi67
uYmR3aEDF21qopdbFO+J/Oha7PJqmMW6u5PTuynmpM/ZUeE4ruirnHtvTnJ3
RIky3aHdRWnyceL7ySmimDw1xaRWgxSno7Lly+b6u8aWqUpMZvdQDlzjHp5B
BrLQgS4wgAVMYIMDXOAE95/Z9qOOdadj9RHmT3JNrWq1x+37+XpTVoctywUa
edOkpWfjOBdrd5nl1j3CinttxA9WqIiPiy3kW/WbKVyj78uj9HfJd1ZHyV+P
XSa/5bpRnqBaJq+tbqko3lYi13gQIzzT2Vy8s2SLqHium8xk1mHn1+VqXLs7
EunKp26OMwc625+bE2vzevM5i5OjX//u3xh/+27M/reZA3qtiu6XaWrdTbA5
dq1zh1MbuAyBdcHrKYbikow9omSvXooAk8rCLNkoyTr1dry7eCq/qTqRj/gu
n3+YclA5cI17eAYZyEIHusAAFjCBDQ5wgRPcsOGP1mFKqrf500OT9tLC0n3u
VYKcDdH9BYV3VzrrPXvnrD4lRtavzwVRm9pUUbdRJ+S7mx+SP7fe5Npq4QSJ
LOOkpGqqJj+ySxfevlt3Xmamzw9s/kLS1TxJsi9EX3Jm0WDxCdJS8X6Vtjy2
S1fxbYvmIt7hjOzJkEOcQiNCGhTfXpAUc8jee+DZXq/YHP7eOqxn+2cDWwPr
2XvkHNYRjPbz4u5fGyR7Kz7uYh3rJ06eppBnplrITQfulLw7E8gXXjvE/7RY
nYgndCZBOfYkLZonha3dlAPXuIdnkIEsdKALDGABE9jgABc4wQ0bYMtv7TOq
sTLXdbhpWS46tM/TKS1bfZSu4McHo7i5tcEym6vmwuqE9uKJqhFy9QQveZRc
IFns2JzvOtuXX2ERz0vi8viN5cf5maJq/sbiC/yU1NP8jYMHeJ8uu/huseH8
qmlOfEplusTl2njX7uOey49ZvxGumSEX7a/4psDvcGuXdR3qpEe3eQg2szms
ZuvwPNvLkR/4Q/jvTOaDjrB9hLWA9/l+W5bMi5QKDyT1ERt5WCiaT9aWlFT4
8J3vnOXbn9cnrj14cuXBWHJJOo8cXx1BqqZEk2+uxCoHrnEPzyADWehAFxjA
AiawwQEucIIbNsCWD2PKiovDTbRywnr2CYjPuLRII2fOkjOOKVqjuEMtK2UG
ox4KDw65K5rtXSUX1J1xnaXSii90ieAjdhTz/vsa+XdGmmTIKCPSQseUHNC3
Iqc9rcmtvT3JbM+uRJvoEqf3KqTW6gKffGEHb3nTk9d/uU7iHre5IOdgR3l/
/+binoeiC55mdlfO4Qy2DmewvQx/OJ/FlF/tQwxsxfz4bOaLkth+amBrYiB7
r47xZuLki8aKuyrbJeort/DfemuSfEOeBAdPJZHaUUR9YiJpCNpNzDpKicxN
QZ5fK1YOXOMenkEGstCBLjCABUxggwNc4AQ3bIAtsOlX+77LyjX3qTLY29Pu
kG1D8XRB/CwLbub0bFlXSQeRzfwykZ1vvXzCpTBJ3aDR/Io+BXzro008N8KI
NCtwJP6H3cnTr0cR2fUJpG9AANlSOJXUnJhENuePIys3e5OVp3lybKk52ThA
izSbUMvviVrHJ3to8hvSh7huerJFPsyih9iCzSHWYTHby/CHLVhMQVw+wnIb
5GDaLI+oZLHwa+bP9ZhPUnE97lLC1gbe75bvYYmbtJDfrd2Z1DiOJEtiIkh8
9RZioi4lN9ocIX3Tz5EDR6+SbNc7ZPi7+8qBa9zDM8hAFjrQBQawgAlscIAL
nOCGDbAFNsG2h0keZgFB3lZ7LhvYB+2RCByNrgpuRlbm6w7fJBSXnxRdevJY
PrcqReL/bBk/vuE8P/q5Ntl2TUAaWvuQMQOCyL4FS8izgJUkIH8NaeO2nmx5
s54Uno8jxXdWk/t9I8lp8Xxy28aXNDT1I36V3cmD12/5E0GZfJcmG/5Ah1Wu
8WwOsQ6L2V5+yvwhYgricinLbTqy/LCB5bHIxZBP3GUxMZ35dfgm7K97bI30
Z+9ZPakHUVk1kcQ8jyV6D9LJkU5HiLRDHTEpf0jynr8jI4uaUckmDbp1paZy
4Br38AwykIUOdIEBLGACGxzgAie4YQNsgU2wLWL9Tou+4WXW+yzb5Jw0rpAe
HnqBS9zrxm0sbise01At75cUL3l8ZAU/ybqe79jYiXSW9CfDAwNI+INwMj5h
HUmu30Zmbt1DbBdnE3f/PLLdNp/9LXPJwaB9ZKxBGrHSSSQLI6KJTtoCIhWN
ItahDsR2R0syakWBcg7Xs3WYy/byWuYPCYspiMvIba6z/LCY5dhLWS2AfLY9
y8mQVyA2wr/DR2GfYa3gfW+OWUf2a0uJ/O1pYqzxgKy+okJFKzTpD2N16anB
hrTlwE40Y3AX5cA17uEZZCALHegCA1jABDY4wAVOcMMG2AKbYJuZ2a49Yu/h
dln6TwQpEQO5+lsPZDlVOuKx3U/J/eSuktV95/JViqv8ZaeuxPaIF1m7dC5x
3RpDvt6QTKYvyCY2zJ/0WnmcbOp2hpDgamI18DypyK0i94oqyKA1h0jzZQVk
ReVuonolnly9EU58lvuRIg9OOYdYh9jLnswflrOYcofFZeQ2yA87shwbdco5
Vk95s5oAeS1ys2KWX+xlMRJ+Hr4K+w1rppi997Tic2Rv1FNyd18LmvOdLv3K
pxN19jOld8Ks6LFEWzoqw145cI17eAYZyEIHusAAFjCBDQ5wgRPcsAG2wKZ5
eal2rW8Je32vbpvV6C/Ma7m/XlrABYkKe64qvKjVynXTTmd+xpnj/NOehuQg
9SCTBs0ndZfiyPvOu4l0URHZdKyCRP5QR9643SV6+Y/JmMgXxCTsJbm44RlJ
fNhASkpvkLwF1aQk4DA5pZNLtmdsIenZy5VziHWIvbyX+UPEFDMWl5HblLL8
EDl2LatTolith5p0P6urOrDaIJXlt9tYjtaD5RmdWKyUMX8Pn4V9p2BrB+8/
K1aDvvfRp2FDu9P9kTY0/KQTtdZ1pQfcKS3x76McuMY9PIMMZKEDXWAAC5jA
Bge4wAlu2ABbYFPDo03ZB2962D3R0xHcODmF0/Mxc+5/z0R8n6opJq/PkYy+
l8yXpbYkmw/yZKUghAybsZbsidlDooaVkkT38yTS8h6Z5vua1Lup06XNNejc
A5r0zkAtmprWiibebE6T7VTo0x1PyPn3V8kU7XJyrmu+cg6xDrGXfZk/RExB
XBax3EYlWlu+i+XYtqxOQa23jdXLpqyu12a16UpWX91mNYIvy3ORqyHfCGIx
E34fvgv7D2voZzYP6ZNM6aS99rRrR1f6OrofdWwaQNf0H0Qjp3srB65xD88g
A1noQBcYwAImsMEBLnCCGzbAFtg0/4q3YMiGlMwdZf1y82L18pcFxYpq3zwo
NBxEXK/bevJrWlzhjbJ6kiTV8aRd0EqS0SmN9M0rIfONakizEw9JeokqvX1Q
k5rZ6VJhkgE9eNCYlk3qSM8sNKKTrTvQE9ltqSCkBW0b8JpoZd9UziHWoRrb
y/CHiCnxLC5vY7kN8sPjLMc+zeqUEazWW8Xq5cdx5Y7el9SkIay+92Q1aiyr
s1ArIN+VsJwNeQdiJ/x/NPNh2IdYS/5sPu5b8dS8wp2mTvamCU9G0GU+o2nl
8rHKgWvcwzPIQBY60AUGsJTxh2GDA1zgBDdsgC2wyWuDmlSjfqLDLlkH5+Uj
U/LPjzATvyxsktcVhktyAhP4/a81SP39fiTTfRG5Ik8kqkUy0qrqLDl1p4EE
FqnRY53b0miBIb21qxtVaTKngZlWdGyINV3Zy5K6dTalBrs70YpR7albtIZy
DrEOsZfhDxFTbrG4fJzlNsgPo1mOfYrVKa1ZrYd6GT0Hhfk2R/SX0CMhrM73
Z7Uq6i3UDMh7kbsp8w8WQxEH4MuwH7GmMC9tEobS+pGj6ak3vrR9kD81SJ+s
HLjGPTyDDGShA11gAAuYwAYHuMAJbtgAW2BTyAM/Jy8NF0GySgyX3dpbmL/m
tUjtyQG538tWfAv3w3zquK5kWdsxxNtiFfGu3k0aDY+S7ak3yd6g9+TJT63p
2UVGNOScKS3fYEvb6XFUkiCmtVGuNKxUSE/vdqRHH1vSqyO6KufQia3DZ2wv
wx8ipliyuIzcBvkhcmzUKaj1UC9HX9MQo29T6dgkRY8uW19HhF4J6n3UrKi7
UDsg/+3HcjjkIYiliAfwaU1sX2Jt3WLz853DRNrrXgCdHBBMQzJnKAeucQ/P
IANZ6EAXGMACJrDBAS5wghs2wBbYtDKb4/wOGeYWVZhwvUoGiOq3HygQJFSK
N44fwJ/rcIefOMuBPIsNJk8LN5DZ3+SR54oqMjPpCSkNa0k77e9Abwf2oG96
2lP7Ja7UOMGNxo7woDdjPGmLJnc6aFJvOlOLU84h1iH2MvwhYspAFpeR2yA/
RI6NOgW1Hupl9BzQt/EyrHCe38HEeYKCcOjVNS18WIieCer+YFa7ov5CDYE8
GLkc8hHEVMQFAfNt2J9YY5inw1kz6GrJHHo3Yp5y4Br38AwykIUOdIEBLGAC
GxzgAie4YQNsgU2v1lEu+EGctLlqZX5i1mWR/sJIuWdug2va1z/yD2+8559r
UuLALyJTpVvIzx2KSTO/y8Tpu7fk7Zo2tGlvJ9r/B2t6PUVEBbVfUVGPoTTg
9Dc0csVo+mjtCLrqjJdyDrEOsZfhDxFTNrG4fJflNsgPkWOjTkGth3rZq/kL
yQbVMnkfGzUx+ofowb69occdeaUjDnu8S46+E3onqP9RwxawOiyL1RLIh5HT
IS8pZbEV8QE+DvsUaw3z5X9qPvXqvFA5cI17eAYZyEIHusAAFjCBDQ5wgRPc
sAG2wCaLtgbcFOltabkhL5MY64l9d1XJw6ztJC2CVvPd7rUkx466E+PapURR
t4P0Lj1InqXfJOUyVdomXoc2DTehnmoOtMi/N23hP5hqTRlLtXZOpl0WTKUT
dk2gD9kctmTrEHs5ivnDsyymIC4jt0F+iBxbzuoU1Hqol9FzQN+m3nWjHP1D
9GDRx15W2YKLeWcpRt8TvbtHKQd59FDQB0Ati3oMNQXyYuR2yE8QYytYnNBn
vg779Q5bc5i3N4GhyoFr3MMzyEAWOtAFBrCACWxwgAuc4IYNsAU2XY5txW2f
3jwvPdlPtsLDVBxR+lxedtVdYvDDel5ltBbpGutJTt8KJ+rGaeSY8AjRDbxN
jFmu4jmuPZ02pQetXSKgEVH9aMMmH1o9dAJd8nomVejMV84h1iH2MvzhOBZT
Sllcvs1yG+SHlizHRp2CWi+J1cvoOaBvg95X09hlcvRg0cfGWcDnPH/pbP78
TVXyJjYNl5ld6iJumXJPHriWStp1i+NnOGuSjQM9iKpLOHn2bSpx8j9Mflh8
i5SWqNEJR3Spj6w7y5sc6cD5femwnkOp0N2XLgkNpkvZHGIdYi/DHyKmIC4j
t0F+iBybZ3UKaj3Uy+g5oG+D3hf6h6nVUfLka4dFOAvAecrnvH8T2hhwgQnH
pKuDjWRHZjUTT8/NlW8fbyDxDonkh89vRtKbuZE1pxaTZTuSiebgUqLx4hqJ
sVeh3rXtqM+grtSYxd3AAJ4uW+1Jf7YfpZxDrENNtpfhDxFT2rK4jNwG+SFy
bNQpCazWQ708JX+Nsm+D3hf6h+jBrtLfJT9vdkeE8xScSX3O8eNuHOXeSJyk
16eq56+q2iFaN9pQ7hIX56pdO5FXbHnO29YKie2quURPO5FUGciJ16saci34
Fel7VJMq5hpRVUVPOtPema4J6aOcQ6xD7GX4Q8QUBxaXT7I5Rn6IHPsW2/uo
9VAvo+eAvg16X+gf8nF5PPrYOAsYvNVQjDMpnOt9zvnLsSyO22bWRbDAMplb
sO2scP3hWFHDcC35sx7WfIjbBX7tUwui4udPWpSsIR73M0lCWQV58PN90rZC
narH6NCGnV2oMN2KzmJzOJWtQ+zlSOYPEVNusLj8E8ttkB8ix77D6pQgVuuh
XkbPYVv9NpK5YImyf/jWSJOgj42zAJyn4Eyqi+NQ2YCkbOnnnD//2ODnVHg9
z7HfjvZczbtEl6m9Ooo9Jj6S7x5YLqk0yubPZuoRnRhvcuxpOPnBcAfxLi4h
79deIpOXviTnWmrQyFftlXOIdYi9DH9Yw2IK4jJyG+SHyLFRp6DWQ70cf6xC
2bdB72v0gKBferD7GpVnAThPwZkUzvVK0rh8nC9/zvVbBKvfRnALs67m9c7N
W0Jkw7u2ENe1KZAv3t9OMqbnYn5jVRPv/RVHhmwLJg+q4kiOTSbxXnacNBbf
IGNHv1HOoRpbh0VsL8MfIqYgLiO3QX6IHBt1Cmo91Mub3c8r+zbofaF/iB4s
+tg4C8B5Cs6kcK6X1ugsxPkyzug/5/7BjCvegq/GbrAL7CkQ+NTs5iZb7hJq
OOaKtIzd5av8dXjOsZSP7WhIgsYNJolLlpCM8M1EdXweqX1SrpxDrEPs5T7M
HyKmIC4jt0F++I7l2AdYnYJar5LVy+g5oG/zc+fdyv4herDoY+MsAOcpOJPC
uR7ORnG+bLkzUpARMyTrc+5fPXu0KXuSycVe+j8ucfhxbJfc481byA6PVhXf
rSqUrz1mJtk4MpRPt2zks0Zak8YN40jq60iydPxW5RwOYesQexn+EDEFcfkA
y22QHyLHRp2CWg/1MnoO6Nug94X+IXqw6GN/+1yb4DxlpkorXjXBS966NlVk
sXWPEGf07+ra5fQfU5/5ufdPbVyqbciOE3aXSyNyB7iv5maPuuKiMlJVHOJx
VL7DrlZiPTaFPy5pxtaNM1lWP4GksDnEOszGXmb+EDEFcRm5zTyWHyLHRp2C
Wg/1MnoOakUykt4pjfjMWKvswaKPjbMAnKfgTMqp7owrzkZxvsxZu8vuTd4s
wLci+N7mc+/fz7SqsXS7tdHWpHKd4xavHk4z86vyJaHzREFPlxXaCRrFz8q6
8tlcPp9dpKGcQ6zDzWwvwx8ipiAuI7dpxfJD5NhHWZ2CWu89q5fRc0DfBr0v
9A+jBCHKPjbOAnCe8v2zZbzfpTDJTO8qOc6X1abEyPCdw261pBytLV3t8c3S
535+pN/lW/M3XmHW4T/tzIzKjnXsG+vNPR9uXJDw5prI7s58ee3Qpa5uEQ7K
OcQ6zGR7Gf4QMQVxGbkN8sOlLMdGnYJar4jVy+g5oG+D3hf6h+jBoo+NswCc
p+BMCud6tr718gND7orsrpoLtZ+9c9bMmyaNT/3eAd8sxdQUWX7u55fRGund
s/aZ71rf0WgfaXbbrlN4P6nunKfc0YzQgj5jjcWbB++VX2RziHVow/byXuYP
EVOGsLiM3Oa9r78yx17L6hTUemdYvYyeA/o26H2Ftx2j7MGij42zAJynxPSd
y/dNipfgbNR6fpnIcNRD4bzaYJn87kpnfG+zeeIme3z3dcAjOO3fcH7ubtHT
lAvbb32kIsJOsCLD8bFsgzS7RycX5+uxBb3ZHNqydYi9DH+4gcUUxOV4ltsg
P0SOjToFtV48q5fRc0DfBr0v9A/Rgy1+rUFwFvDtvWQeZ1I418PZKM6Xu0g6
iPCdA74V2RjdX/D+elMWvvvyqNSzwPeH/4bvN/AbNDqp5/mi1TYvv2nu8Hwn
Fbwx1szLYXOIdZjI9nIw84czWUxBXEZug/wQOTbqFDmr9VAvhzhrkvffahH0
vhpvvOerOtzhm7sf5nEWcMPWk8eZVK1WK1ecjeJ8GWf0IdOzZTu0RnEtR+kK
8M1Sjfa4fTpmZ/ZEfTe4x7/p+6FOIcIeI9toWbTJumqzKsLNHnOIdYi9DH/o
ymKK6shfcpuWLD9Ejo06BbUe6uXBIZG8drc4Hr0v9A/Rg0Uf2/dlKx7nKUaD
iOs9qqbA2WhulY44bq8bdyOyMh/fiixacsYR3yzxhaX7nuWaWjmMWWz+W/v+
Dd+vCW4Gdm/YcbynJptDrEMntpc7M3+ImIK4PIvlNsgPW7IcG3WKF6v1UC+j
54C+DXpfB6+6S0Kt7SQeuQ2u9gmVYtUnB+QvCpvkl948KHS7ZyLG+fKtWw9k
+M7Bzuiq4H7xdAG+WcJ3X88PTdp7tD7i/83dh7/P+fvJX+fwG7YOz7G9DH/o
ymLKShaXE1lu48HywxMsx0adglovkNXL6Dmgb4Pel0bKPXl46XM5+tgdFkbK
67YfKJCueS2qHmEmxtnoNz5mzgb766X4zgHfiuB7G327Q7b9AuIz9B1uWm5P
9TbHN5x/Zt+/4ftd7OUBzB8ipiAuI7dBfljHcuwlrE4Zymo91MvoOaBvs7Jq
h+jorGZi9GDRx3Y11hMnZF0W4UwK53orRqbky2L18nFGj+8cMvWfCDIt2+Ts
vWxg37fKYK84J6ynYY3Vn6673/4+9+/H8RvA4nI2y21es/wQOXZvVqeg1gti
9XJNXu9c9G1+tEzm0D9EDxZ9bJwFnDTkZc1UK/MVFSYczkZxvpxa1i/3sZ6O
wFfdNsvFe7jdsPAy66Agbyu/rFzzyIvDTf6Jffh9+O8X5rB6CjVpCKvrszao
SY80+DntzOK462sot7+VAXd5ZSvlwDXu4RlkIAsd6ALjv/XvF/BDfogcewar
U7S2Vduoz6rrNanlHLuK9cKsQ1npjpLVLQStq82lvhNl0p/H3pfOfvlc+t2i
auk8l2jpodH2uWeCHQUWrec4XHxUkqln62n3o5GoV3ezXXvw3Re+nftU+z78
+RcN2bU1bd2eH8u/tdXusyJzQLs4e31FkcOJRSNyPLNa5c4dYaccuMY9PIMM
ZKEDXWD8N2368Odje8ciemO5VWoPacbOugT7yviR2QNU1jhWjdZ1EgR6OeVZ
+Tqd7+Xr1G22l9ORQF2ni75rHH0ujcwe8zrB/tqV3IzOsyut1L3ufNQH/y/9
hi+06h5vUGklVm/sFXb5mV336HaCdrOcpVm+UueWrnbc5fr1eTGHLLlm18pc
NvbWF2LgGvfwDDKQhQ50gQEsYAL7r9px+kgba7tvb9s+iunkECxzyGm1UNeJ
F812Ssv43ulRzGSnresmO0n/SwNYwAQ2OMAFTnDDBtjyMXszrcZ3p56zLdfl
K3q17FRjP6wyQKDuUy7dlZLIVe+xys/I0xZumXRDlCeMFR9efkpc5H5dfHPR
HeXANe7hGWQgCx3oAgNYwAQ2OMD1MXtsmd2jSh86Dvy6zGnOxat5Y4obXSS5
QuGbWXbCYeYOwlciB6Gm+L8zgAVMYIMDXOAEN2yALX9mK3d3U7fs5z329KrN
3DcmvsnRYJ1HroH2Ge5lW7EszfWF0NR6lTh3/nkx2WFSYK/SRzFYmKqYzMsV
c9uUKQeucQ/PIANZ6EAXGMACJrDBAS5w/plNj9nf3pvZn6ub5KI3M73AzOEr
8VnSIF499JZYsuS22Kn0tnhY2W3x8E8cwAAWMIENDnCBE9ywAbb8kZ2jRy83
6apYY2PTRWSX9WqYoObFE+fymBfc9UrvgvCBY8V32yaLy/cKFduF2YrGE5qu
92qSJCOHmfAmDv58hk64cuAa9/AMMpCFDnSBASxgAhsc4AInuP/Iruls//zA
1gDeY2/3Y6LSuxMUF4rvK/z7lShy+5QpuriVKRQOZYqZnziAASxgAhsc4AIn
uGEDbPk9G53ZGsB7nNEyzoyv1xKkJL7iPPq9kIWElAnfhZaJg648ky91XqYQ
XlgnsXEI569PfMZP1rQiRxsGkQGDJhHzuJnKgWvcwzPIQBY60AUGsIAJbHCA
C5zgdv6DdajJfNB4to9M2Vo4wN4nurk5Xzd1PS8fF8HXTIjiL/WN4nu6RfGP
2XjxDwd0gQEsYAIbHOACJ7hhA2z5rX1ZzAflsn1kxdYC3qftBT2XvFWRBZuM
t4p81mwUq3dbr7jk0Vui/iie31XShQRlTCLHFWtI9/zdZJ9+ETELP0ZuVVYq
B65xD88gA1noQFeJwbCACWxwgAuc4IYNWb/jDwnz4/BF2E9YE3gv0teXDHVc
QGIzZ5FvGuaQ5RfnkMWX5hC1ujmk2d8c0IEuMIAFTGCDA1zgBDdsgC2/ta83
8+P28EVsP6WyNYH3mj39muhxO2vxDM0wRc5OfX6abUtSx08mrolJRCAuI/5t
bxBt87fkrb4GNa5pS0376ioHrnEPzyADWehAFxjAAiawwQEucIIbNsCW39qX
ymLhT8yfwydhX2Ft4P2yBhwm+bvPkpvDTpExC06TwODTpNf002QEGyP/4oAs
dKALDGABE9jgABc4wQ0bYMuHto1gecR6FgvHMn9ey3ySJ9tXWBuP2Ps1nByu
mGQ2lh/ynQ3hU1eShAoFiZt2l9xV06AvOhvRrVo9afYuBzrrtpAu2CxRDlzj
Hp5BBrLQgS4wgAVMYIMDXOAEN2yALSN+k9sgn0BMhF+Hb7rA9hfWiIy9Z7+U
NnQvp0cNYnXpT93bU1nH9nRkp/Z06l8ckIUOdIEBLGACGxzgAie4YQNs+dA2
5GIaLJ/owGLiCebXZzPfNJTtr2C2RvCe994JyRzfjUT3bCWJ+E6VrnIwonoD
bGnwnN70vcCbljSMocTne2odNEU5cI17eAYZyEIHusAAFjCBDQ5wgRPcsAG2
wKYPbdzGcrKXLK9AbIR/h48axfYZ1greN22tkEZ3orTIlqeWS3laHcbTeWzM
/ciADGShA11gAAuYwAYHuMAJbtgAWz60TcTyWR+Wk+mzvOIai43w782Yj8I+
w1rB+7o0qyZGrTWoTkoPeqVcQle1GEYfiKbQyPlzaaLJIuosCKMp0b8MXOMe
nkEGstCBLjCABUxggwNc4AQ3bIAtsOlDG5HXIjdDfoEYacH8PHwV9hvWzCr2
3u/CJ1CbGwH0QrcA+vjbAFo+JoCe/siADGShA11gAAuYwAYHuMAJbtgg/WD+
PFhNtojVBKosr33McjPkF4EsRl5kfj6I+SrsNx22ZozZe6/5uic16+9GO8WN
p9Hlc6m/XxhNjWHz1TWM8pWhVGfnLwPXuIdnkIEsdKALDGABE9jgABc4wQ0b
YAtsgm2/nT/kaMgznrB3gr+fxnwW9h3WDt6//4DFdHNwGJUnhdEzyWH0wkcG
ZCALHegCA1jABDY4wAXO4b8zf3xhuZUJq6tQG+xg+e095Ggsz1BjsRL+Hj4L
+w5rx5y9v1/WRDpMeyE9sDmM9kgJpRPjQ6n9uVC6pTGUDn75y8A17uEZZCAL
HegCA1jABDY4wAVOcMMG2AKbYNsfzR/yDcRM+H34Luw/rCHMwz1JKN24IZR2
2BJKu3xkQAay0IEuMIAFTGCD48WfzN8GU2lGW1abXmL1lRmrESpYnotcDfmG
hMVM+P2VzHdh/2ENYR7Mp4ZRbnoorX0eSp+qhFHJ+1Bawsbj/wxc4x6eQQay
0IEuMIAFTGCDA1zgBDdsgC2wCbb92fwh71DGWeb/zzEfhn1YyNYS5iP/cSgd
2hRKx3xkQAay0IEuMIAFTGA3+8j8nT2aYJ/J6vt9rEbNYXUWagXku8EsZ3Nk
eQdip9L/Mx+GfVjK1pIzm4+ZamF0FJujejZU2Dz93sAzyEAWOtAFBrCACWxw
gAuc4IYNsAU2wbaPzR/yD8RQxAH4MuxHrCnMSwPjfvmRARnIQge6wACWMi7/
hfkzixiZ3cLVjkOdP5XVqo9ZvYWa4QTLe5G7If9ADEUcgC/DfsSawrz8/Cdz
9+v4+T9zCB3oAgNYwAQ2OMAFTnDDBtgCm2DbX50/xFLEA/g07EusrZd/wT7I
QBY60AXG3L8xfxWPYh0v1a/PQ68E9f59VrOi7kLtoMPyX+RwyEMQS1NYPIBP
e/qftfUx2z5ch9CBLjCABUxggwNc4AQ3bIAtsAm2fe7zF+yq6xR9yJI7tPyU
GD0T1P2oXVF/oYZAHoxcTpmjsJiKuCD5G3P364AOdIEBLGACGxzgAie4YQNs
gU2w7XOfv8m2Xk7Nr5W5oGc3hZcrujv486j/TVkNizoMtQTyYeR0yEuSGn+J
D393/qADXWVuw7CACWxl3ce4wAlu2ABbYBNs+9znr/ryeCf0jNH3nNemTIH+
E3oo6AOglkU9hpoCeTFyO+Qnj//B/EEHusAAFjCBDQ5wgRPcsAG2wCbY9mX+
/rfn78v+/RI/vuQvn56/fMmf/1n+/KV+++f125f+wT/vH3zpX/2z/tWX/uk/
659+6d9/Wv/+y/nRp50ffTm//LTzyy/n5592fv7l+41P+37jy/dDn/b90Jfv
1z7t+7Uv309+2veTX77f/bTvd/+tv8/l+/H/hR/qKcJq0jhW16M3YhoxMrv8
Uawj+pxTbL2czl4erxy4xj08gwxkoQPdD2uyv/L7P9XZnX0=
"], {{0, 80.}, {
80., 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSize->{32.984375, Automatic},
ImageSizeRaw->{80., 80.},
PlotRange->{{0, 80.}, {0, 80.}}]\), 3, r, Method -> m], {r, {1, 10, 30}}, {m, methods}], methods]], Spacings -> {2, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/7398edf9d4d34ba3.png)
|
| Out[18]= |
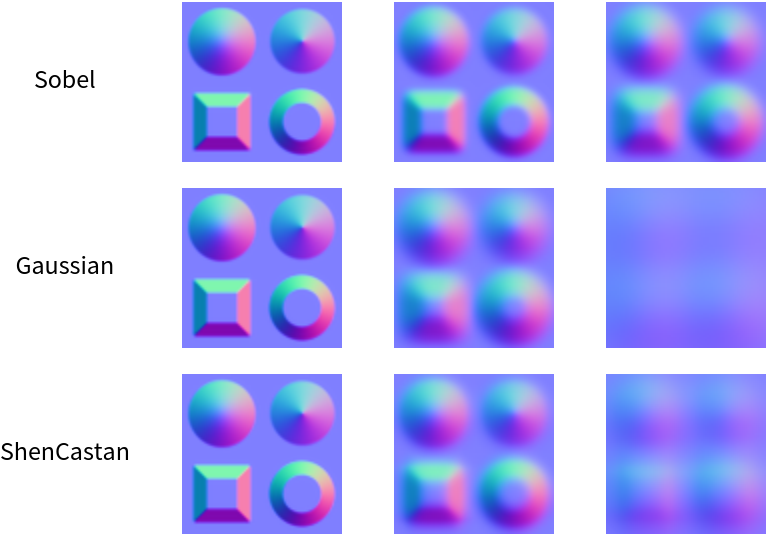
|
By default, a "Fixed" padding is used when convolving the input image:
| In[19]:= |
|
| Out[19]= |

|
Pad with one:
| In[20]:= |
|
| Out[20]= |

|
No padding results in a smaller image:
| In[21]:= |
|
| Out[21]= |

|
By default, the channels in the output are rescaled to be between 0 and 1:
| In[22]:= |
|
| Out[22]= |
|
Use the range -1 to 1 to leave the normal vectors unscaled:
| In[23]:= |
|
| Out[23]= |
|
| In[24]:= |
|
| Out[24]= |
|
NormalTexture produces normal textures compatible with MaterialShading (requires Wolfram Language 12.3):
| In[25]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/b91e552b-e1ec-453b-9c6e-65a0382d72ba"]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/3c0fd71cbf9f8b02.png)
|
| Out[25]= |

|
The red and green channels of the normal texture correspond to the horizontal and vertical derivatives of the input image:
| In[26]:= |
![input = \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztmgtM1VUcx6HymfEQxygzvS4fgM4Jci/85Z6DxmyIgo+wkqxIhZyPUFNg
ive6LFRCVJgamI9JBoIvVCRuQmkZPtq0sCajGJSPzFYuFa9t2PlcuZtjyrCw
xn+e7bjjOb/f9/s9//85v/M7/4vhjbcmxD/i4uIyv7P6Z0Jc0oh58+JSJnbk
P9PjZgUGzGIwoKk+LPotOUElAeeTBwV207rvT0p1NUVmZpmWNZQ6Km36GMMG
2/9br7PkB/ULGDdheNAm++/Dfug/xJR9Sgvpa/PRuvsv16om52teIw9o9pJP
HZU2fYxhgy0++IIB1n+t//KqXYGb/3zB+KvXRyVjHk0PbpzrpxmO7dAiCsO1
l1OXl/WyjbItrU6zVVaut62v2OKotOljDBts8cEXDLDABPtB6/9KjguI8Yk2
Lj7hW1I3KcFUc2Wk9kt8lrZv18GyDLdVttO73Wz+9trhHcbmhXZb29VcPNNo
7vRdpKPSpo8xbLDFB18wwAITbDjgehBzOLtt2zBDrydNlw5FlT5l2hcyxCdX
O51wuWxa4kKbPdkztH5yL/Peglyza9058/RaT5Hn6SvWpQQLy/AwR6VNH2PY
YIsPvmCABSbYcMAFZ1vOodY9P2jV8jrjiO5bS9/v8ro2dtl7B3vGLbHN9gwO
ze053ezqd8FctNFXjPprkrj62mJRKDPEyeINonzGFhEXkeeotOljDBts8cEX
DLDABBsOuOCEuy3mEPLj9aAjmW4HyhfGlX5StU6zf2EvS+gfqxXGDDXvjLxo
3t4vRIzY+bbwPZwtVnoXiWMNFeL73qdE4LQaUZD3syg8ftFRadPHGDbY4oMv
GGCBCTYccMEJNxr+7XsoVzg9UrxKtw36UDu2I9wW//jA0EVrNpqvnekrEj1n
i/wVG8S8GwfFkcAq0efaZZHg6ior1naR27095E8pPeTNXd6OSps+xrDBFh98
wQALTLDhgAtOuNHwT99LtVqbGeq98kzAyxgfY/v8Ynqo1wfHzQNqwsR4/xUi
57E9Yu6wKmGMuSauKH2G3d5yX41BFjf4ybKaoTI5xSgbjwc7Km36GMMGW3zw
BQMsMMGGAy444UYDWqrvc78cVbGCfcYa5f1WqmcD7pGoanPSymgRtTFblN+o
ENdPXBSpMzvJ5PM+MnrPQNkh0yhl+Ei59bdI6Zo1UXpcekmu3RzrqLTpYwwb
bPHBFwywwAQbDrjghBsNaEHT0fuIY8Q9Ygb77Sb7Qb1nnhH4y5M3iJKOlSJb
PccTap24G56V1TlGebj38zLHfZL0Lpoq37HOkVNyF8ioxBQZG77IUWnTxxg2
2OKDLxhggQk2HHDBCTca0IImtLVmDpxDqSqGE/+eU7GDfcea5X3zrOBJTbeL
k2q9D2/0k3PcwmTR7IlyiSle1h1aIHs8s0R+OcMqG9dYpf98q1z96u1Kmz7G
sMEWH3zBAAtMsOGAC0640YAWNKGtNWclZ2q9Oo+I5U+rOEgMYf+xdnnvPDP4
9o4dLD3OhEv7gFh54Y9E2e/NJbIo3SqTDFaZXWaRqz+2yDEHLDK2/HalTR9j
2GCLD75ggAUm2HDABSfcaEALmtCGxpbmUKBynEsqP+Bs/UadS8R04iGxhH3I
Gub9a+rZwVt/coocfHKBfHGqVQb3scqlmyzyibMWOc1ukRG3LLJW1atNlTZ9
jGGDLT74ggEWmGDDAReccKMBLWhCGxoLWsjHolW+Rq5DnjBVnbE56nwithMX
iSmL1X5kLbMOeIbwd0izSvfPLPL8cYsMc7XKr5XWelVdXKx3rYxhgy0++IIB
FphgwwEXnHCjAS1oQhsa0XqveWxRuectlbftVzkP+QJnLecUMZ74SGxhX7Km
WQ88Sw+l41KdRe5WutKUvlstzMFZscEWH3zBAAtMsOGAC0640YAWNKENjWi9
1zzIo8lByd/Ifcgb/NSZy3lFrCdOEmPYn6xt1gXPFD15rdDfvOY1zQUMsMAE
Gw644IQbDWhBE9rQiNa7zYF7DXeC0Sqf/lblosUqjyMHIn/g7OXcIuYTL4k1
7FPWeFjTe7jfOThrWtMaAwtMsOGAC0640YAWNKENjWi9213snLqjGdT9hruB
n8qrXVROSj5HLkQewRnM+UXsJ24Sc7qdvb3WW7OWWlpjYIAFJthwwAUn3GhA
C5rQhka0orn5PLqq+yZ3Ne453BHIr8lNyevIicgnOIs5xzgDiJ/T7S3v6dZW
MMACE2w44IITbjSgBU1oQyNa0dx8Hsnq7sy9kzsb9x3uCuTZ5Kjkd+RG5BWv
qDOZ84yzIKIN5uCsYIEJNhxwwQk3GtCCJrShEa1obj6P0ZlZJu7Q3D/3qrsb
9x7uDOTb5KrkeeRI5BeczZxrtW04D7DABBsOuOCEGw1oQRPa0IhWNDefx7sN
pSa+B3CX7qzuodzhuP9wdyDvJmddo/I9ciXyDM7oq204D7DAdGArDrjghBsN
aEET2tCIVjTrdR56WVd62ed6ibt6OQf1kpdQ9JAnUvSSt+vlHqWXey1FD98Z
KHr57kPRw3c4il6+i1L08J3aWfTwu4Gz6OF3nDvfS3v/Xc1Z9PA7p7Po4Xfn
O0t7/zuA5qW9/13GvUp7/TuZh6Xty98hpCH+
"], {{0, 50.}, {50., 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{50., 50.},
PlotRange->{{0, 50.}, {0, 50.}}]\);
normals = ResourceFunction["NormalTexture"][input, {-5, 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/78c37327a4ecc223.png)
|
| Out[26]= |

|
| In[27]:= |
|
| Out[27]= |

|
| In[28]:= |
|
| Out[28]= |

|
NormalTexture calculates derivatives similarly to GradientFilter:
| In[29]:= |
![Manipulate[
DynamicModule[{input, normalTex, normalXY},
input = \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzt3Qm8rW1Z1/E3UrMys9nKBsvK5tIGK9krG2yetHnG0qwoTUuxso8iIKMC
AsLLCyKTgIiIyAwiIiIgk4iIiDghICAg4gsCtr/rvL/3c3m79t6H8x5Y+5yz
7s/n3s/aaz1rrWc91//+X8N93df98Z/1eZ/xObe67rrrvvAjj/98xm2++NO+
4Atu8yWf+RH++ezb3PaTP+m2Xnz6cb/LdYd2aId2aId2aId2aId2aId2aId2
aId2aId2aId2aId2aId2aOejfe+L/u7Rtz7hCUcPuuGGbd/39Rza+Wp3ufOd
j17wPX9r866f+1+bn3/XF23e/74v3XzrEz5p88Drrz9g5dC27U53/PDN+977
fze/8J7/vcXHe979JZsbf/6LNy99yT844OTQrnvqUz7l6CUv/vtbjLzhp/7T
zcefeet/3+LlQTd83Gbf13ho+21sD7jAG+++8Xabn/yJ/7jFx/e9/DM2P/2m
/7L5/lf8483DHvrQA5dcw+3bnvjEI3zxzp/9wi0mXvvD/2bzjrf/j80LX/C3
N/jlOd/xaZtffP/7Dxi5htsD7n//ox981T/f4uJtP/N5m599xxds3viGz928
7KX/cPM9z/+bm4c/7PdvvvzLrtv86Oted+t9X+uh7acd65Kjl7/sH219Glzi
+FOv/5zN637k3208/42P+SObr7rHr9vc4+4fdeCSa6zFC3e8wx2OYINNwu/F
Iz/3zv+5eetb/tvmNT/0r7Z88shH/IHNve75MQeMXIPtmc/41KP73uc3H9sb
/2/b3/sL/2drt/KB4eZHXvtvNz/2o7fZPP+7/8YxRu55wMg12O5339+y5Qzc
AR9sV7oGh3iOzvnR1/37rX1yt7v+moMPfI01/gw/F3/wZ2BF7AwucEcdl/CF
+TmPftSjDlxyDTWxdrzBl4ENx7e/7fM3P/5jn7V5/U9+9kZsXn/VD/yzLU68
Lu769Q95yNExtxy97KUvPfg5V3E7tkGO4OHNP/1ft/zBVnWkU/gzr/z+f7L5
gVf+0y13POuZt958+7OOto/f9Mb/vD0P1/B52DLHNu2BW67CZo63uJm4CPvj
LW++7ZZDxNDEWHHGs799s3nKk//85jue/Ze3/9NJOIYO8l42zA+/5l9vvu7B
v/vYR37MAStXUTvGwzb+jktgA0Z09gmMvOL7PnNzjKMtPr7l8X9qixXxNHoH
Jl78vX9v6xP/xI//hy1W8BBuwTXf8exnH33F7W9/9IiHf8IBM1dwu+997rPl
kXwaR/YGHoEPGIAJNguM4BH9O5/zV7avidHjlbo4LXzRRT4X3nDNve75Mcf6
6w0Hu+UKbHe76123cTPY4LOwQ/ADecMGLLBDHvuNf3Tz+G/+k5vveu5f2z4H
J894+l/a9ic/6c9tvu2Jf2b7WPwETswXi6/gFNjjN4vRPvpRn3jglCusffVX
fdUR2yJbNVsETuiQ533XX9888xmfuo3Dw8hzv/OvbjGie15/2lP/wvboNTYt
TPGD0juwhm/wC5zs+zcf2sntQTd83BFMvOTFLz66y50/8pg33nr8/0dvx7t8
AHYJ/eB/8TP2CNmS/RO/9ZO3fAEz5n9hJE556lM+ZcsjXn/Ct/zp7flwh5fY
Oexe2MEvPkeu277vxaH98iaWQU7iZNdd92Vb+9JjOHDEHfQMmfJX8Ig5GvYq
HmCrkj0b5Luf9+lbneJ5HWZ0+gcGnOdz+EnZtjof2nt/5LWvPWDknLTmZ3EH
DMACvhcLYW/80Kv/5RYHcCIWwrb0OozQEXCk0z/sCTIWC+Gz4A9HvAIvuMLn
wYLPYPfiI5+NPxy9l937spe+9OiQX3B+2v2/9rfdbD/ifnHS5nbN14lr6OmZ
5vT0niuvtTk+j9ka9Aks4R+cQT+xTx19pudhBT7wjPwT/c5f+asOPs45aD/4
qlfdGqeTK3njgvCge25iIizM7r3hp+PE0Jwb7jn/ww8c4ahX/+C/2OKDnhNf
Mx8ol018d9/36Fpt3/TYP3asV37siB1Jp2R7GNtkyDZtXpfMZ58YKi++83qO
7OOUcubDkv99V/M9YiRia09/2l/c8sfDHvr7Ng/9+o8/1kU/ccDHHtoxrx/d
8MDfubUr4IFc4aOx73EyTHfs4o6TcLM+79xwocOPDjMTNzqssmf5zvypY3vl
CM/t+55dK409Chtsxakjki9sxP9TH8QDq4xnjyf0nut9k2/mZ0zbxnP4JFyx
T8Rb933PrpXGZzkei0dP+rY/u8nm0MlEDyswQm6tuXP0+rQrTrJHen7aIWHC
c+Gl+Er8EWbE5HAIO5ZN67Mc333jjcd20o23Pvg2H7zG3rMe171PdsXAkmu2
ZDhJ1yTn9NGqUyYv+D/Z9/r6f++Z3BRvuQ7X2Jwy+6TzxObe/ra33fqQe3L5
2ryXt//yX7Fz3O/igV08sdoWJ9ms8/+e26WP4hG4gD0dh3SEkbgEh7FpdbYT
rPtNfOEDr9zyxs777uc970i84yT9sAsjZ9mlu/CxYmTFxewrRuBi9pMwwh9n
o/z8u9518HMuU5NDKuaQ3XkxGDkNHxfDEydhI52xCx/FZ+u78CGex1ZxTbDy
lXf6COu7Dli5Be3YdzySw0Huxt7FYORi/drTOOIkXExsrPiAiTps7MKHLvZv
DXF+kPnFO97hww44ucR2/QN++1ae7vG0TS8FHxerP3Zhor7aHpMvwkR9xcbM
dWPH8tu9x3Xc86t//cE3voRmbYN7ChfuaXHwW8Idqw9zEk+suJj9LHvjJGzU
6RrX4Bw4cQ69c9e7/OoDTj6A9oD7f+yRuXa4cC/d03IKbwk+Zox0l32xCxfx
Rv0keyNM7MJFOdW6c8Xqi5vIS3Jd3sc23/e9v1KaOdLsz9a/FDO7XBi5FHys
tseKkdOwUfd+eQjyFpo/xpMem58+zA2f3d7y5jcfpVuaWyWb4qbFrOb8yXzu
LL/lLIystscuXJxkj6ZL1i6foM6H12ECVtgneAVmdHPFh/XnJ7fj+34k92vG
wFtL15r+XfMsKy5Os08v1v44jTdWfEzemHiow3z9JHzwd+Q0yTv5qde//pCP
dEJ71Df8oZt1ChkVRycnciaz5lb9H6+kl3bhZ5f9cZpdepbfsos70iM4Y+KB
HtHjDn3FBlyIvdIz8OEz5Daat9y3PM5be8TDH35zbhCd4f6HkY7kRGZkXw0z
fc79Xkx84zS74yy/ZbU1Vn0y8YAv4oxdvAEbcMG/kfOoy09y7iEO+0ub9Sfy
LMzBkXU5GXAw59qSR3NnnRd/NAd7lj26yxZdsXGS37ILF5MzwsMuW6NaBLgD
b4QNua/yZnV+jtfl2lvvt2/ZnJfGTk2HrDH1mUNGnmRDdmGj+db0zlnxjZNw
cZpPO3ljtTFWXRIuVjsDZ9QnPuTQW4NufaAcajn4/W+dx75lcx4avSvXvJyP
fJWOM8eweff0f/ZJMl9j5RfDGRMbJ+Fjl70xsTF1yuSM1daoT/6AB9iw9qu1
oXACI1//kN+7ESvat4w+1G36/+YpvvZ+v3XLGWSRr5ue6H84Ib/yvMjHOC12
MjFyMfjYhY369FsmRtIvqx067Y0wsgsfrbfxuLxougUWrK8IG9busFnFEOVS
8fX2Ka99tfz/b3/Ws46qLWUseRwPFO/Ihi0f0DnGerUPySl9BCPlOhc3r6am
40nzK6fFztMvq59ymv86sREecEZ6pW5uDz5gA5dasxM+HL/5cX9im7+2b3l9
qFtrpNSge9EL/85WnmRDZu4vmZHvrpzjsOI9ZJYcyA0e8o8nP8QXPrfvOSvG
sfotMHKx+Ji8kZ8CGzgjO6MOH3LT3Af4sLbLWlExIuuHH/dNf3y7VvhazJWW
12mM0B2toXQ0dtxvcgwTM6e4I75o/WXj1GOYgK8woYcTj8l9F2dMXTLj5uHj
tNjX5A19+rDxBr7Ak9kd2R74I3zM2gTwYX2oNenWXRzj/prjEuvo6AdyMp7c
H+vwjR/jihzSNR17nJ0RFpzbGCWj1tzGJfFH+mbKf2KgvsZH446wMW3S6aPA
anZovAEb8cXEhW5NcfrF77dmy+9XqwJGxAIe/ahP3Dzm0X94802Pfew1hZFv
ftzjji7kid9uO4bcN+uV5BK5V+4PeZNrdmscAlfpjtY2wEDranXj13inc5wD
J/GH59Y46OqbrDGw03hj1SfT3og7Vmz4zbAhDrLiw29Xh8CcDYx8wyP/4OYR
D/+Ea2o+WP0n94vMum/ul5pSju6TtXbFkYqpNl+b35J/0hwOeRrH5OKeO5J/
9mk6BZ52+SMwEA56vCsmWlx02qJTn2RnwEa+Cl7EGSs2sk3pFphQywSH0DE4
lS0CH/ZGuVZqDqgDcve7/dqtvMm/GlHuFWy4t9V7cXTP6YQZU49LWoedXnGE
CWOb70gWxq8xXt5XducaA90VB519tUNhY8XHiouJjYmLaZeyPfxu2MCjxoaO
T+MQtgi9fK3se6EWCL43hpO7++w+uqfGmfsNM7jX8639LzbGxq1GXWtsYcVr
sEL2cEEu7r0xSnblajiuHLHGyGc8dJe9US9+vkunTN4o3hE2qok08YFH6Rjx
EDxibtNach1GjK19y++D1fJz7e3gXjaHO+dpyQ423F/j0GPy8Dx+mDH37It8
lXRJaxLYoOTpM6oXQibGNPlXyy7ZO4YT/1eXZMZDV1t0tTemTjkJH/FGfkv4
oFOqq4Y/Joc85Ot+z1bPPPD637G5w1f8So+vGi65y50/cvtb+LeOYsl0K1zg
erIlc7H3YqrZofhh1v+YeSRxR/Gvk2LmxdbIsPp3cJL+Kd459UbYmL7r6sPm
O+XDnuar0C0rPsJGtkf4qHajWICuTh875MEP+l0bOd+6vDy1EfYr2cvXrK0L
H9pX3P5WN8fLyXTmBa3r6sLDaTlEZ+UIwgkdRd5kyQYgF5xOLuRIvuQ+458e
V5sqHyVczPgGvqhP3og7skfpFticPovOLnUd9Ap8hAs+Ll/XPijsEGve7XlA
16hfYo+Mfcr1cjbrWXv8/a94xbbeFHxUv7/53PJ/1lygGTvbhZPmXdIxa2w0
25S9gR/gwZg2jhu/5Ea+MBBOVt9k9VHijImJcBF36NPumPioZie7NP6AD3Ey
9gds4A86hh1yzL+be9/rN2zrjbNHjj/zqsFI64me/KQnqb1/87r+7IlZj6F1
1eV9nLVObvq/M74+52aLe8Ck76cvyJk8jW82YfW9ydZr6RAYKA46+7Q3VkxU
Q0/HIbCxCx/xWHYp/XKsP7bcARvVssEfbBAcYt0NnFjPZ//Qfcv2crZ73P3u
2/3HqjcFA7N2f3Nw2Rk91//6WfmE2Sa7co3hpLru6Q9ybo8AsoITciNLsq5+
M57Ivph2xoxvTEykV+rVW5z48H34w3dmf7DR6Bf8AR/yAHAIfNAv9/ma37St
W2K+5hfe856jq8lmNbfgvjQXQ2btUUeHVF8uWWdfhKG5DiLMOCfb4yR7tbh6
8/fN07NL6JPyd6qbWSyimBW7kszjB33li2IccJE9mi87sZFdWtwjv5b/Qr/g
D/jgv6iHFT7oGDxCv3zNvX/jlkPoGXWypo13pTf3nHzJhz3QPnXTbq2Xn1p+
M24pJt7ak+ritgYrnQIX65qFbBHvnTEQPgsbFE5wAjmTZTLjbxrjxn3yDw8r
V8xYR9gIF2FjxYfvcV9gkn2aDULH0C/wwY/R+bs4BD4c2avq8uxbrpersbNg
gnzgo7qGdMXExMz1KWck/LA36Ab3mzzpjVnLbuYCwUD5rTPnOIzABz/YtRTz
Kl7X3ND0P3WyxYO+v30E6tXsnX5s/sr0W1ZsyE2Fw8kf9EvYKA7Cz3UPcQgd
Q9eIsaoHuG/Z3pJWbsPPvfOd232D2mtsrvNvn8vmXmcN7vJUyRIm0unkSM7N
6ZVnEgd5zCaFCZ8fRuY87WkYaQ5g+qFkSab+J2d8AAfOCxMTG82xwFU9fMQb
Ex/4Y+oX+MhGhQ05efQMbOAPtfbEDp75jGdc0RjRjsfLEX2NF/gRxdDLIcue
KN9w2qblsxdvZeuSKXln21ZnLPsjXdO+mc35z/l8n4dnwkgx0mJebIzmh6a/
wZYkU7LFA3SQ18PAxMW0Rdd4enExnxd/0C8TH3EHG5UfQ7fwZdSbEDfDIXwa
+8vuW8a3tOHM4tyN6+Ig2aX5Lu011lwYOZZ3tsZZ4ay4e75OMRCYaG4+fpl5
QeWorxiZcY65DwlZk29yrfs/vMBAc29hY9qjcUd+C2wUH2uen/2RbRo+8Ec2
CP6gZ3CINTZ3vMOHba6G/ZL8tnLBZg3U8j3mmnt8zw40Bo1HdmT5ztPuqK5q
Nm1Ygwdc4T3wAWettY5j0jnFSGApXVM8rBxBOqd9acIJOeebil+Q88SK7ryJ
Da9l06yx0+zTbJDsj6lf3EMcgj/4MjAil/Wn3/SmKx4fmnpN7tXkj3LGim+Q
b3NuZJQNCCNk3vqY5m/wgmOxtfBG35A/PDRvfKG+2BfdXEtq5gHgNn5N8y7F
Tl1DXJLOyR/BDWSd/6GTd1ihi7wOF2Gj+RbYcl7YmPyxCx90DBsVPu5x94/a
YqQuLnIl56C1BkLs3by/MV2N5TXOXoyD3LNf80mNdfZEcVT4Kq7WZxRLgRcY
oat8Bl5g4/oM56w+8IyRlPNRvH1ihI9Trk92J8zDAnnPWLnH5A8/dMnUKZ7T
m3eZtcDpF/iY9kdxEDYqfKhTk52qjiRdo97XvmV9qa15GfOR+Bw+jOPyTpuz
K1e92qjt1TDX0HQOGTcXgzeyeeGiurgekz2dQt64CFe0hm/ardO3yXbJDlox
kl+brZFvghvIPD3hGFZwS7hIr0x8wAb7dOIj7mB/hA82KjsEd8AJW5WeOb7H
Vyw+8nfhpHW61TSedWJ21f+YdmlxtXyc9o2pTkB2bLHV7JMwQs5ki1dadxOX
TF0z1143f7euWyhvsBgHexSXNK+ST8IfIXN4gQHPwQxc0Csw4rlwUfyDbsEb
cUhx1HQM/rjTHT98q1/YqT/7jnccfcvjH3/FYqSmTkbr47JFsiuKa8x89jhi
rpOb66fyjdNXzi/mnm2CF/AVXJAlDuga8oGbs8n/nXnKrY9rnh9GsknaT+Q0
jCT74hqOngsvze3HG6t/O/UL/uDDxCGwgT/e9973bm3VK3VNeLWXxXXc82yQ
5u7Dx1zf3fPZlcl76qT0Sp/VOt41r4jc6RMxDrYAPihnIP8336ZYGpyUi9g6
7KlvmtNnR4eRbBI2aRhp7r7cDjxA1uQOB5M3pl/r3HrYwB38l4mPbBDdvllX
ck3Or7zTnY6MxWyQ9960f1A6Ytecfs+TXbXvqiHSHlLVplnX2WWHtA4cB/BP
+SHlx7aGZuYKzDhJ6x7oG1wy9Y25u/LUyyPMD4YRWGwOv7lZ9kR2ZjEN8vd8
uUGr7aGHC7oFNi7EyD5MLd8N/hCvpm/4AfuW86U2/EdGjXtyJ5M5b5/POzkl
jqi24Fw/VwysWEpz/sk9m5WNQWckPzzWPs7FR+Z88DoHXI57MbXVdsUlzenP
XEJ2a/P49AqM4I5iXewIOae6/2EHHpxT7CO9AhPzfD4MfMAF/mCHsFXtd79v
WV9KO77H230uy0Vtvw94aP4u/TH39pjz/c2/kZkxXgwWzugRdgTZZoPAi/Po
CPIs7o0DZn58tY9mL+couyT7dZftWp5hdmtxknybYqXNseCJ5u7xQL4IeZM9
foGL1W/xGp3iPO/R8cfEh/3or8S9KeQyG0NkTobVfGg/1GLtcUv2wa78H/Im
G3IyxmFm5gSRY+uhyktlm5IbG8F7m6eJY3z3/J5pl8Ql2a/TdsUlzfOVW1Kc
BBZhhO/WfNy0N3BEcytkDiNk7Uj2sJMuCh9hAy5wh6PzL8yJvu1IvR77e+1b
3pfS7GEcZzTvgk+KgcYrxnZzKTi8PBz6vrFaLAK3e479CQfkBh+wQ2at2ytn
zPiGj+K1cNKanVn7oTVXE5flDHhP+e9hZNquK0aKpYUR+ChWyt7AE3CQ/HGB
+kM62Xs+mwN/THzUndf73viGN1yxe6qVW5btsavWQ7jA3Xi8NS3FzMJX8/rk
AyPFsPgV8AIb5MN29Fr5YT432ZeTtubJr+u815yBmZtWHuv0gVsflf8bj2SP
FDONR4qR5pskZzkf1mDKIfMcXLA92CL+D0/4A0Z++DWv2Z5zpdZTfNANNxyl
24uVus/le5Cfe+zYvH2x0l11q2Y9q/KGcAd8sBHxTmu7ybX6Is0jz7mdsFe+
fPpt1gxZa4c0D+A7xWonjxRLy7eJR07DCJsEV8BAGIEP+WM/9OpXq7W6jXfA
BN5wDp3kMSxdiDO989gXePkVu7+r304+xjw7rpiBIx2Cv6vFXOxsxlzJD3bY
BHQJrOER4xd/iFPBRus6dRxTjL3P8h0n7ZWZv93cEJzsqg1QPrTvz78p13Vy
Wr7NxEhrcNkk4qZ8WvYIXZP/yp4gc9gg85e8+MXbWId1JDDjNRhxHt74gVe+
csshuESu+L5lfanNGMHt7qcx5F65f8bgWk+GnIqXO7+8wGyQ1te2BrK1uOUl
JWOyLc8MTmY9zomPNfYfTmZcPt/GNc0YfbESv2PmpzUPzCbhYzcHPDGSX5Oe
YWvgBbKnX2AEPr7n+c8/UhtC9xhWcAqucXSuo9ev5Brg4kbklp6Z+YY9x/5r
P1vns+XdM2MLJ4tDue/lAerGbbkj/COPZ058Nsbc22jdK3XFSWtwZozW586a
AeWn0TfZrtUlK05STsnME4ARc3Rs1uxVvxOHFP/KFsEZMEL2fNm6//EG/eN1
74GrY713xeLD72hfVPfbvXUvyRj/ihWIG+HQ733Ri44ecP/7H93trnc9xsaX
bbnTWix6GE6qpwEvbEPj1xhv7OfPzjylYrHljbTGYu4rsOqbaausumfG5mes
JP+mmCveY5OwW+nUFSOtkWoun31Bh+AFtggd4n5853Oec2Te4qlPecrN/bue
+9wtPjzvvj39aU+7YvFhPbf7ZTyyHdwjHItX6Vj7S4oZs8XlXMKF9TWOX3Pv
e2/vh3vm/OLOuNmRHsfZ5FCMnT2i0zHFYKsVUY2IdBOZNyc46wqs+763p3Pz
iev6irlOq/V8M4dxF0aar5mxEeOAzshWdX9wBhzYr0n9JvlC9gfU/Y9XvKbO
9b5lfantWHbb/Q7hAj/qfhM/B0eojfi197vftt/3PvfZHmHmGx/zmKMXvuAF
Wz3DfmmdU7nm7rO4gdqb7hN7tTkdMU05GsaqI9mQEd6H1+rb0hNslWpYlc+4
csm6j2ZrhGc+Iz7JLpm5aeW57sJIsXh4F/MQ/6Jn2CFsDhzit+FR2FAP/2EP
fej23nWv3CNzX/uW8y1peITM/WaccHyfj6xfbx/juXasmhL4w/ihZ/GHe2jM
mTc3d9qcWWtW3Hd87Z4bs8Y0HxRGcJDvNkbNf5hXay6PDMVN4AVWspPax2Sd
T/Rcr8Ur7aPq/XDSOnCcWZ5rtdro1XID+L2uByeW8xE+HHEIHUOn4BFjBkZw
B10MJ8bXsW67ImPuayN765HP8tuLDTY+3Ddc4R7iZFwkNtncqFgDTOAN/gGd
nn/ADnRO65HgLb/RZ7GL2b+t76YjyJi+YHOUE9nc8bRv8qHDUXZOWMEn7BJ2
a74N/7c6mGGkuZqJETwL08ZIHMnWoFvg4oHXX7/NCVG7WQ7itbrnFVuMLI39
m/bq2fr+7DscjTe6x3yDeBuXwAdceM79p6tgBf/QO/jI5+n4yWfxObyeHUxP
0Bns0nIfm/vjv7dnUrGW6s83/+x95VLjKpzFF5OvGo9U92FihC0CI34/PYND
8Ic5DD4LTOhsjzj3Wm0zhuhI7jiED1lc1viHE/cYr7BdizvQ8fQ/neQ9eKLY
CnnRA/QQXtHxTGulyFFsz+d7D6xUM2ud+6uOFuzACx6Br+oXie2ImcBJfEff
sEfwYbkg/N7JI/QMnLDn2XPXKlec1ORNuWfGeHkSMKKLRbqvxn7rD8ovN07z
H3ALrDgHntgczsUVeB/OWnthPMOJMUtX0V+tk9PZm84T++ArlU+CN8o5ya71
uXRdcwHmcmAFJtNrron/jktwH3uk/MJiq3QNG/XYrrqmueKkxgZrHpzuYDvo
xlucgQPIIdtVZx9WA8YRbno/TOEGvXnYdEtzRc7hV7AP8RDe8hzMwQyfqtp5
ZI9byl/CJewQn8mOoNt8P2xW46g6jdkldA583rTH9zY2Im4mJoJHjnXYAR8n
tG945COP6Adjrfmu/EP3ktzZD+43XdAafTIgD/4snSJ2jwPggFyyG41j+IMN
nOA95Rx4j/PxihgFf5Q+8x6f1XfFK9UOF2/xms+FMxjAW84VK6leGizyheEO
/8G634cr2dS+Ez7Y7Ne6vXFac5/JjRzmWvnWQTu6v3i79dWNb/qjGq3VG4IX
OgAOyhusHghOYR94vhp2Ycn4hhW2rcfxjmtxfrGa6s6wp8XDzSHAg8/3erWF
YZdt43m85HfRN+xWGGGfZ69eTbVkLnfjGxvf1URv3mOt8+P+0gWw4nXnsQ3L
TfOcGInP4cuwZciaTcimcS58XKij/uk3z8tVO9p3+z444AeZe6UH8Fp569mg
MOc7LqxTuNX2moq1wGp17nAI7MCx3wPjMMK+wlfwhUfExvYth/PcxITIuJpy
dTIj7+rR4Qe2AvlUT8rz1aPyGcU7yZm+yJfGQ63nxwnGPQzhepiBL3FhY994
Z8PqbEvxOLKEM+8rv91rfDEciG9grXx6MRdc0jy3aypeDyf5YT6DvWrd877l
cJ6b+0zOeKGcI/zvnlbjkvzggU5oHxL48dycV6s+Xf5LayK9x/9ww06kT8id
rOglY90Rv7gG32c+hg2RPijXp/zS8grZFnQfXmqNOZ+YT8OOhRP8U0091wJT
zdlcS3tDXGojQ1iIO8oXghG8QH7Zf9Ubq86D3r5hHjdHX8f3ZMSXwEO4Q5yK
/qdPYC0OK77KpxVzJVc6hKy9TqeQJ3zBDF8ET4nXkXnX6fO8F++wuVtfk+9e
HSN6U16AuYp9y+A8N7FD96ycv8Za+sX9njW04YPsey2ctIZhzs+XL003sSla
79baKHKrVgj+Ly+5nGQxWz4PfvCd/mdDiHvRD7AGL+ZXYI7tg2fwFP3EV+GP
+Q785TEbl12F08Tt8Iz5h33L4Tw393HWByrOEQZmpwOqXVg8bGKj/J5ynSdO
PF+uQeO5dfkwUk0q76nuumvh43o+zPBtYJps2cLNHZYnRn/5DnqkeIlrcx3+
p1v4NK6hdeA+Z99yOK/NHDB5sDcmRiaH1P0/93ExrstJL6bqcRgpbm8Ms0Hz
f/F7aw7YF/m5fBjyJjefnd1AruU28GPyu3ABzomfnFcevO9Iz3hMV7lWuAxr
Hldjgg7btyzOazsex0d0OPuwenTu5ayrPWtp58tU73Tm9GSntPYGTqpBZtxX
S4pc2Q/kAiPGfnlLcFB+l5ivuJjn6Ai+TLUU8QD+8b3sHbqLvB1xDizxbekX
mHH97C3XgjdcK9/H0fvEka/Udf4f7EYWxZnKwWgdBNm3Dq71VmvN5GJi1cSt
ruWsc7rWHSMjYx8umgPi4+ICPhCOMYfDNmVjwBAbxNj3GfxV58EifcS+oLOq
ReQ85/gfnuDSNftd1WHU/R7zxHSZcw/65pe3Y36/NZmZ9xBXaH1kORj0Dn+l
nJ1qLO+qmzz3LW1/CH5Fc3TtARRmYKK8akecADvGPZnjGLYn28I8gNiKz8cn
xXw99nq52ThJvI29AW/4AWfhJ7/T7xDrY+/AMP5srbLfAW9yRPYtl/PU5JzJ
IQ4j1W5o/0McAjM4BTbc47l3Rz18zH1mJj7WmoXZJcVJ2CLiaHglTDSfSKdU
H+aCPrjVzXm5xr3uPfDhffiJneJ7+EZ4kp3ju1w3rhSDhQ9zg+aQ/d72foev
fcvlPDWxp9ZN4NzqC01OKb4+bYxqBtXXGlNz/zC4YA9Ut5AucCy3iJ1ZTRe5
Xx7DQbnqdEy2JxyRobgojsEZ1XUw75JucYSpahuKfxRHc+3lZIu1wT9ct74C
R9kbbt+yOS/NmMMh9Ip4FZwUw27dSnMo2SJzf6hqr1fLoboiEx9rTd3WCFav
Dk7E1siabVrdW3pEHBVGyJ/dQm+QeXYsOwXO8YvPaF8QmPA+8m4OCsfBr/N8
PxxnF3k/HMIUnSdWcjXU3b0cjQxaB0mv0AvVFWy8kzc9k13SPnNzH6BZN2jW
Sp61tOs+1zifNS/5IGwQ8scndI/4RvtIlQvkOb6xOAg5irGKo1Vzu3W6+AWm
4BGGy6+Gff/DTnVm2EI+31EvF/pqqHd3OZpcGmOuOhzGML7nUxinuN3z+Lv4
amvHp53aWqf4ozr87fUSFsIDfDhv1rITsyBnOgRGyJ+8W1uLM/jErs8aBrmE
naM7pzxLPk17ZFaTxnfDOf8NfqsRAJfl2umeN/dzodbMlVtb9XI2+7Nag6Vb
e0MGxqmx6H7T47AhlyfOqd5ltXPDyLpXw+SQMIJHOi+ft3P5s+VHkrk4u+vR
Wwslj1DcHWZwSvYK+wP+4Nl1tZav/Tqbv25NGF0HD7gHLovvt2aEPXTIFTi9
yQenR9xTNl77ppaH0d7ZuCRfBlZWHskOqaby1D9hZtbPZVPgLvzW2lucxjeh
X+Cm+UB6BhfgH1j2Xrzku3EaXYjv6Mjwwib3XHUF2Dh0DIwU5xX39b2+Q4xx
37I4j00uuHvm3oo7zbyAdA5sFI8nC7ZINun0ZaYtMvsufLTGgl2Zn9vYbo0+
X7b8dZghV6+xLegYsdg+y5ENSpe5Zr8Fzst/hm3nlbMIb/BBh8EIfXOl1pz5
YDf6hw6gX+SdWi8pbweHNzfTXF1+cfVgJj4mX9RhYvaJj2r4syn5J/iEf1NN
u7X2A1l6DB/iHz4vP6Z4MB3ot8BFPMcWhqf2N4NJNnO1A1oDdCH/4JAfvzb5
nPaQNK6qm07OYqzucesx+ZLF3ott4++Jj1mnf9br39XDyKy1S+50yKyRGV6M
cWO9+BvegSv4ai6XruSDuX72Cix5v/dWa8b7ugY6h+3Mt/G9MLhveZznpr6E
PHk2orFKRhfqfX30Vg7iC8VGslfj8ImPyRUnYWJXb0+Q1kyVp18dTPI2b0zO
ZO7aqkVER3mNP9P1NR9UjZHy7/FH+0oXs4F7//vewzzf2c16RnI3HtsjpjmZ
9h9zj+HjJFtjl/zr5ay2d0g1/tubqH2W218ZTsi1PFTdY895rf0BqisSJ5A3
Wwe2cAi/CF7oGr+h+LHfQp/6rfQWXjystzm94YS5R1p7drqP1Qkq/s4W2YWP
XZgID+0PU85r+4d4P52WHvO4dd3VmJn7PlQX0bnigXDcWqtiY/6HkbjEe3xm
OqnYjyMb3JHf7DPUP963LM5rI6/mVtil7ls5JcZdtmoxq4mRFR/taTmxMfdP
NqY9D0O4C1fxR8Qz8rF9R/mM7VPWXqm4g4+D0/BC8ffWIvtcukg8pbWp1RRu
P8fmMT3X3jjiQq7vsPZmd1P3nE1C55MJXJQT7XF16cr/Wn2UyRmt22+vmGq3
t08IboAXGGv95jrP3H55dJDPyLZtTxmyb70e3925cOy91brwPhzYfAIOgQs8
KYbSvvXVZ2y9hevctzzOa1OHRXzeGG8thbh2Oe9zn5ipX9b9xqr/gTuqS0a+
7Z1MztWbIJvyH8NJ+z77zvZrbb627/K54qRsk7m/Ih3imlvrgTfEfaoFPPMf
igvhktatVo/nMI9zchO3mrUb3G/3lLzyZ/Jt5/518FFec/GI5mfb/6P9pYzT
bBAyWfeCL9d+7vs9a2y6DjrOZ7Ye3We5HjiszkH5tekRsePyuauNBYthcs5p
3pSnfcDJjsbuY79Vf7vc5mpKFFOdfuvcbz19kh/bfjDtmZwMjdtyVcqJnHlv
5ayEk3Kb4pb2Cu/787d8R7kmfotrghWYaF9zOIGxOA1u8ZFrq6aK7+M371se
57G5r63TxMvGWHqm9eOtd2i/wvY6TZe0Z1D+SDWW2ZvNx5G7zy5/Onyka2Ze
U3vV5IunF3TXlS0Mx9mfPj9dgj+yq7zmnGkfw3pz0Xyn/PKb4v0HnCxNTMo9
xCGO5JK/Wy326r+s+43FG2EjfJTb4/ViMPVVz2Szzjy4cIJHHMMMboBfPCE2
4nrIHQfOdUNsU78FtvLdWsMaT5ZvrxsDfoffar5v3zI5b81cKxmQDWy0ts69
y7eEi3WPsbk3Ybk8HrdXodeNT+O2vU/WXt59ubOzz3w415cfXs0An+17XUP1
QLtW145jym9go3h9+u+4DUaza7zeGkJz4/uWy3lqcikaS2xQHMHGyAalS/It
28uwvQlhof2R22u9PQthCoeQd/kG9dYL59tUAw9vkOvUO8WA6/kzMECuxWPN
8ZgzliNjrsc1lZMPF97Xnmuuy2eke2DG0TV77L37lst5avIF3NPi3uEgfkju
9He1surtre619qvzGG7IBa/j/V26ZrVJ0i0rTtIzM+epWAr5kyus5lN53N5V
Yq+u32+RV9Xcst9rTsc5fm81knTjAbbE9Pctm/PU1AkXw2abmIOdc7Eeu8fN
qVXbNXxMzJRDSh+xdcs5uFiM1E/CSDnY7btIL+K+dGDrtdpDHG4u7M3x1u0Y
KA4799+EEe8rJtf8tM/7ugc/+ICT0eR4qhkmXhI2wkn1flf7wz3unPaqo5Pw
tfFOh6RnzsJIdseKkfRNPDPXgvF/YYKfUq1hthI7auaxOM45gfIZPC7211rB
9ufwuTflzB3i9Evj+8m/wS1qz8sjkHMqH1n9cXWRYan9CsydOpctYN4V3zcf
k895MTwy/Zkwku26+jjF11rzxXfhk9AT2cxxmuuZfpnzWleIb4r5sHVhBHac
6/ULrz38wCWXqclXpt+NSTKGjdZjFBc5DSOrLzMxMrETrxSzb71x+4BV/9Vr
1ZKHizjDkR5sDsr/5fTDWjFAz8EI3XRYu3V5mhrsxrCxWW5PMfXqlJyGkXAS
Djxe6/qtcfrWDcIFO8J3V0tPLGTuw9e8U+s7mmeGIcdyuNnt7Nzya9kzh7mc
y9PYd2zE4hHshvbRvBhds3JJGAknK44mTuIR3wsneKO5gmIe5SbAQfNQ5byE
nXDjvfwguJeT4PG+7+/V0NTnZ/eROXnBR3GP6duchJF1LenESOvx1pqhcDJz
sukatiZsFOvDC2xZNnV1bZpXcL30T3Vi6clsWljxPn7yYT355Wv84uJb5Nh+
Bc3lTT6ZmCmmNueBq5mz+kXZN+WAtB65+uKO5M6O4OuwW9my4QZmzBGU71J8
lu3iWJ4LvLRPks+4Uvd/Pm9NXN84Nq6TX3Ur2ne8mkqtgSj/beKg5+Er23fW
Z5trCde8E7JuvVfxEF38uH00yn0p30VvjzX4KR+bXy8uxEfa9729Wpp6wTi6
XNj0DHmGEbI2f1itHPKu7jj8lF9o/racFvlC8hfk23p+5jHMvdPaF4suaR63
GCuOq46WTg+FHzzRXjfVFG4derWmrU3a9/29Gtoxfxy5/+UG0QfFR+S4VTcJ
LmCkWr7W8KobUpeH3V58avbq7cfn2ONqjagbUH1H2ISV5gBxAgyIz1cjh76h
R9go1cGZe3jy4XXvga0Lufn3PGDkMjXyqNYAm6S6sHRLuJCDb52g2jlq6bRn
TXv+VvN77llf9z61VcJTe9Q7rz2s22+vXLrqkTQf6dg+0fIf22ceXtgfxd/g
qLmHm2pEHmySy9CMP3ZjNkk1P8s9xg04Ak7Ka6oW54y1k2+5a+UP1ekZOshn
wFm1z2AMhqz9bX27z2i9Mhu1uWxx1db1ZHeEj/wduMIhYmo45/j7DlxyGZoc
HXGGfBm8oT6BvaDJkl3h+fxVnAMf1Tojy9nxQOvSZ/deNkj1A6yN8D3qNuGU
9qX3WvvkxClrzj2c4Aw2CZ3DVvFaa5LLhzzUnr88TS0RsmV/si+t84IPNgV8
wA6ZG9/5sNWBLocEhxQPKycoDJU/WX6tx+yObB+6BmfhGLwCM3IXyz9pHgYG
2LMwUpytOevWucNKNcbpHDg61Le5Zc1aJnFsNgJctHcimc1YBu6Ye2C1drS6
r8Y7npjriyeHrLVxytsv1xm3TF6hj+gm+Axn3iue1jpA/kz1pKvP1x4puMXr
bJhDTYpLb/bVJh/7rsIG24PdYHzji9YRh5G4o9zD1o2WP1TdtfAw8THXHs+1
g9UmcZ7PZ4/gMjpHPQ180roQ3+Vz8Ef7t/U+GJr71MqNdrxQZ+2uB4xcYjN2
2Y3sUPJtHs59J/+TOCQeWWtGn1Sbb/LHWuukmAh70+Nq68EK/xhO2Ef+b88t
dqzzXVO5kOzZ9lqr5hKf50INgzscMHIJzd6wYhwwUT0q45H8y/kIH7sw4tzw
sdZunHVwJm+stQvikrVGQfYt/sBrOIVdxFdqDWC5SuWu4Yv2veho3obeOcRJ
Lq1ZNyxeTvbGKHuVzP1PNs3h1MNP+CieEodUa2/WKVhrJO2qZ5GuWWsbNLcL
l3DC5+Efs4+9Rq/Ahc63kReg83d7ni3SHteHNTgfeHP/xDiqN0DXk3+1sozR
XRwy6wOvHFL9rOS8q3bWrHFiHsYcTHVK1roGus9LD8II38c1s0XSJ8VZ84Gb
5/Obylfi5xyPiQNOLrK9+8bbHTU30/4ijuZS+DLkHTb0OCQbduYbznp8YWSt
hTPrnTQvo4eR9Ew4iVvSQ83r+e7mfVyneZvi9DrchO1qHVT/U1wQhu51z485
4OSMxsZ3f82VtCd0sQ0yxw35K2Gkc8pbbj5/9Wt32R278FFti3CRbbK+r9xD
z1W/z9H1883znZoTbM1NeQpscv5z9tWFfWoPua6nNZyMr9l/7S2ebQETs8cj
0991XPewWOt77vJ1T6qRk86ZtkkcEi4mtvzvM30XHoPZclwd2we7WjqOfq+4
rc/1uw774pzc1Os2L8KfzNZM7u31veqXNR4yY2bN0VYneMXJWqtvF0bWvmJk
tVHma+1r7jqypfBLNSbL72//2urti8Ed7JLdjQ9o7pWcy1FuHm7GTes9P9dk
Tp9m5i7PuuNhZdYvmLVQTqrXt74Wj6y8Un3H1ti0Lqj5RdcJI7O+Ez6p1pYj
P2jf8jiPzbxde8Ow+eiLcDD7xES1ImbNiMk7xVhnLG1iZdoqu+p+XkzNz131
P6uDkG/r812La3Od8QhsuGb2SfFj2HFdh7UVv7xZd1XNQhySHpn26IqN1vKu
8//Tjpnx+IkTfdon055dY60n4WbaLbOOSrUGxM4cq20Mt63zmfUL4MU8ELvE
b3GtB7vkl7a3v+3zt7VPzcdU88G4mnO3KybWtZi7MDLjsCtOWmN5Wp3ps7hl
xUd1H8tnraYbnOAY18CX4dO0HjkfR6zWnINr8r035bodcHLcrEUyjt7/vi/d
zruTYTo7DmldTWNvjsFdHHKxGMk2Wf3jNT6/YiWMnFQ7trhK+MAn1cuKN1q3
0X7Y1VlzPfnQ5jT3LZ99N/lZ5nN/8f3/b5uDbEyRL51MrhMfs65ZfWJkxccH
gpEZYztpT4NdGJnxtomVOk6ZNbzI3vdll7BZqwXcY9fqPXD15Cc96ZrDiH3G
HR9w/489Ih95xvLI6GJjqfhGPDJrQ6y9dXUrRs7CRjbr9HF28Qhc5CO3B2Q6
Kcystajraywfn8gX0D3fWiG/AaeEEePAb68WEsxdi/N9frP7IIeMbjG/IUbg
nmWThoHT8LFL10yMzF5cbc7xrXsr7coxqgb9rpjbjKmsGAkn8QqMVAeQzmkN
sd/QGqBycNs7zLVdyJ18yjWFkac/7WlH8EC34BD6pdzk6RfGIav9savv0jcz
vrbG1SZGJj+s+Ua7eKW+2rSn4SS71TywnEU5z56rPmd2SfUbqx1NL7ke9TX2
LbcPVXvjGz73yP2AD7rFPIX/ywMh07kv8Gp/zD2C1/2CT7JLJmZm7HXmG5Vn
WJ+42cUdHrfe+yyczHXkcCKGam7P0XuqR1BNAnM8MOJ/88PwZJ3ivmX3wWzW
s77lzbfd5uTJBeW7WOcEH/TwlG/7plZ/tzXdre2fdeBPqpe4+jgnxefbhzw+
nznzMw67Sw/NPOk1RjvzCurlsM39Ulrb6XrYYfCRjsEhfkt581drDWA1i9Qi
JFc+P70iJ7V99tyH7DbntIZ7XdO91gOYNZwnbtbaRMVL1nja3HMaHhzpnmrF
r3mNK15W3lkxsmuOJx+nGGx73Zcn0L4L1TXxm1yzGO3YI/aqwglsZHNYk9L6
KHmfuFRszP1o/r89YLpP2fntN946/17bVUMinExemvU1m8eZ9mu9OeR1X/uJ
kxUz8ctpezNNPzm8lBtb3VHYqeZrNS4cXTsMVYvtmLuuGowcc+iR8Qwf7C/c
0Xo3cUQyJgfnyMUJA81vhZXWas7nwspah3VXXauJk5Pir3MeecZTZl7BSXoo
/bMrz3HO+6abYGnG3apBIG7is9yT5nBa7w5L1t7AyvH3XjUYETuGB3ExPos1
t9bTpmMmN6SHT+vh46Q+8bLWL9pVA3zWil/nknfxzDpnvPLJSb7Q9KGnPgpP
5N9+jXBS7XtHv8f1Wssl51Ue/fF1XTUY0dhm2ebs1GqIZWPghmo+nIWRySe7
+tRFu/admDbuxMucp18xM+cCs1925RgUX1ltlelHz/jKxIu4CS5hc+CVata7
Jvj2HXjGWgvz4ce261WFEb8Jh5DDtCWqv1+Nfsez+lkYKuaUTtqlj06yXdpL
dp07PmneeMZr1zjLyjGTZ6b9Eo7aF5KPU2296vDofOXqHT3w+uuvKnxoaq3i
EfLAFXq4YK/qYaT/T+rOO63nI8VJEy/ZwCdxTPOuK7dMnKyx2omVqYtmvsHk
GXgIM/lD1WJkm9A17TPcvlw6fpFPbx+Cq7H2hD2hcTcfxriuDsSKFXqIX3xL
+sTbxElYOUsX7YrZThs3W3bXHFA+0Oo3zw4Tq17qMZ0jXkKf8HNgpJoC6tio
abxvWX4wG46cdabCRJ18YYhvc0v6yksrTs7CyK443NwLacbhJlZWXpncMvVR
dSyq3RpGyoGjZ9Q5sgaYDWuvcfMVV3pNeTb2sTyO7Iltfk4tb7/Lurp+H5vc
PSY3mCDP9l5MrhMzJ/UPhEem/XIWj6w+0Em+0Lpv1km+0KqT6tU5aS1HGCnW
yy7ht+hiZS98wQuOzOG5p1diftExD27xztZQ54Ff6/iWN992W/OBj2sul9/r
eTJ0f9sDYM5r6mR5lr1xsfbKyiGnxVbWmpuzr7Vap52yy3felYs99VPrTeea
sGK7sCKmRq+It7M/qiUAL+pBW5NF99y0Nmvr6zjn+17+8iN7sp83f8f6sfY9
Fu+wXhsW5LLr5vmrP2YNRHUgGt+rnTD9juqmTr/4YvyeNda2Ky67y7+Z80Fn
9ckvcUv42BV/mTmVYWTNt6zWVvmWrlHM0VynLiZtzFlDPOu1Veetbh2S9Tmu
Q3wfltSRth/DPjBCx8ingxGyxxOuEVbUo1OzBWbqfg9eEWddaxuGJbH6Okzp
7ktdbsnFdtfh3upiunr33Jod3fXiQd29Pas7f+19lt51n3StZItnG0fuUd3/
OLfafu++8Xbb7rHn4mS9+Yxem/ezsekxPjc3RrerWfGhxggbBH8UF8tfgX/3
yf3onvgd5nf9Pr+1epfuged1j/2mflfPdf7F9PlZet9X795OnLo291VPdif1
sJ5c1tqdfqvfbIyobTRrNerVsQm/cDXx6XFzWMYcvZl+LDbgXuOZmZtZbn17
QFa/vFpfOp21S47/H8eBQhg=
"], {{0, 187}, {137, 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> "Grayscale", Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{137, 187},
PlotRange->{{0, 137}, {0, 187}}]\);
normalTex = ResourceFunction["NormalTexture"][input, 0.1, radius, "OutputRange" -> {-1, 1}, Method -> method];
normalXY = ColorCombine[Take[ColorSeparate[normalTex], 2]];
Grid[{ImageAdjust /@ {ImageApply[Norm, normalXY], GradientFilter[input, radius, Method -> {"DerivativeKernel" -> method}]}, {"NormalTexture", "GradientFilter"}}, Spacings -> {1, 1}]
],
{{radius, 10}, 1, 20, 1},
{method, {"Sobel", "Gaussian", "ShenCastan"}}
]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/2af0f48bfa1177c2.png)
|
| Out[29]= |
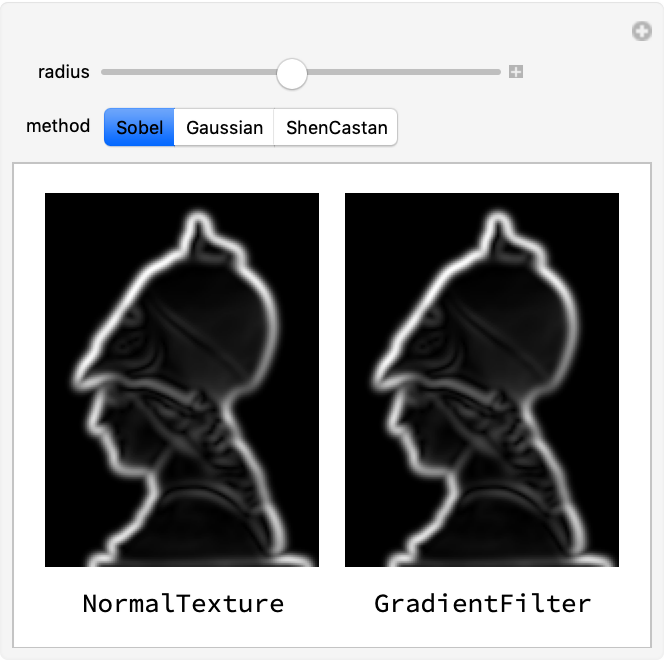
|
By default, the components of each normal vector are rescaled, causing them to no longer be unit length vectors:
| In[30]:= |
|
| Out[30]= |
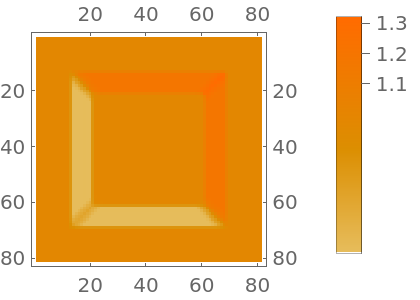
|
Use an output range of -1 to 1 to leave the normal vectors unscaled and unit length:
| In[31]:= |
![MatrixPlot[
ImageData[ImageApply[Norm, ResourceFunction["NormalTexture"][\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztnLFqFFEYRlcl4gvYpIl5BS1l78XSQtAERbAIKxgsomIEg1iMD+BL+A52
FmnFxl5QEbGJIqziKgbzO2diJSLikN1/4XzwLSxbzPnPnTvV3lm+emtl/fBg
MLhzrP1YGW2d2dwc3Vs9ypdro41TJzf48cKvGmOMMcYYY4wxxmTJ2Q/Ph+du
7g3ffY3hy4jheI4LP3MwD3NNyyHXO/7ievl8uSnLP5oyjqbszmHhhp85mIe5
puWQdeO6R14/LnefbJeF2C7f28YcFV644WcO5mGuaTnk/mf9uP7k/Jfy6GmU
SxHt2kZpf67ZCye8cMPPHMzDXAcm7bfsP0uabh3h2HqzWBd2luqzWKp7bQ8N
TqQtfHDCCzf8zDHu9vZ0HfI8YT+wnvDcXjxd336s9VXUGokLH5zwwg0/c+zO
yGF0147CusJ1Y/VK/fZprb6PtZY3X+GCD0544YY/Zuyw/drtD9YXvvWH9+vF
SVMn0bTPngdpCg9c8MEJL9zwZ3DIc4Z9wjrDOWtffyt8+/ukdtzZHLJfst1/
f7ofI7nDWTv6l+pQhxmqQx1mqA51mKE61GGG6lCHGapDHWaoDnWYoTrUYYbq
UIcZqkMdZqgOdZihOtRhhupQhxmqQx1mqA51mKE61GGG6lCHGZrdof/H7ufQ
cwH/79DzKf0cek6qn0PP6/Vz6LnRfvH8cv94jr5/fJ9D//heEWOMMcYYY4wx
xpiDz0/Jk1MG
"], {{0, 81.}, {81., 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSize->Magnification[0.5],
ImageSizeRaw->{81., 81.},
PlotRange->{{0, 81.}, {0, 81.}}]\), "OutputRange" -> {-1, 1}]]], PlotTheme -> "Detailed"]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/327cf03f5037df01.png)
|
| Out[31]= |
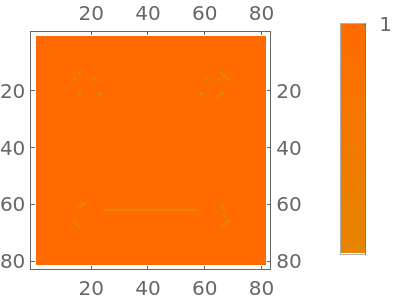
|
Create a normal texture for the Earth:
| In[32]:= |
|
| Out[32]= |
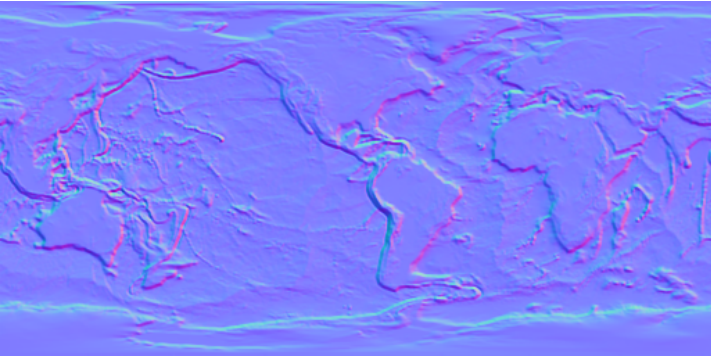
|
Apply it to the unit sphere to simulate Earth's terrain (MaterialShading requires Wolfram Language 12.3):
| In[33]:= |
|
| Out[33]= |

|
Visualize the normal directions across the implied surface:
| In[34]:= |
![heightMap = \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzFl2lIVFEUxycdomyzjBazIsJ2tcZ08s3Mu2SrRREj0QJlYwt+sIUM1CJm
CGmBFopWwwqyD5IZWerYJO2Lie1ZEW1UWgYRLaBU2vnNTBHh597Ada73/Jf3
7j3nvDeD0lc6l4WYTKasDvLH6coev3q1Kze1Pf8sdWXGWzIJDgiOfz+bSkaN
PFC/raRfs9kyqybcUjptu8W5PzJR+xpqDR39PuFN0jDv8D7jvZX62QoGc9aI
gQELBy4aaKHZhtWfT8dTm2LGLkgak+6bF6+/iDkz6MX9MxcW11it5dXeB88H
JqW4DmrVr7vaiuuibUeyA4M5a8TAgIUDFw200ES7Lc/JBQviUqeknuqZt2ps
2aPisqJFG60n6oZ4u2wemJTt/qI9LvuhrZkZ6pv37oYvPb3Zlzbnu38wZ40Y
GLBw4KKBFppo4/G3Z5hci1PWX1U3xEcc7FA+uKbJOmxFn8oraydrlt1PtOPJ
h3w5fc/5OjfMtWvTEx25R/c6mixe/2DOGjEwYOHARQMtNNHGIyx43+x9guxD
hFxTD4lHvu0+riUjs9KUV6ZdXjfu7OdJpb6EK012e9Uzx7H6ZP1yxQb9dPQB
vTyt0D+Ys0YMDFg4cNFAC0208cALz3w5d86A/eDaWgVn7/VUm7ol2tc4O892
urnc0fvDfP3S7UJ948c7et32z3rMNbP6tjPMP5izRgwMWDhw0UALTbTxwCs/
mLcOOX/OYrjsSzu5xhTBT4+ItLc2huhFlh36cvMdfWWJWV0viFKpa+PUxGSH
ur1+on8wZ40YGLBw4KKBFppo44EXnjMk3/tL7pEHnMlV2R+uFd5FS77+8ly9
Xl3VS0WNTlQRJ5zqpi1DmZuyVNauHP9gzhoxMGDhwEUDLTTRxgMvPKuk1s5L
3neWHCQfOBv2iWuG/ym6v7p3YYLaOiJDrYpfrwoaPcp536Me7AsM5qwRAwMW
Dlw00EITbTzwqgr2BGqO/C+WXEyUvOCM2C+u/a7omHetUPNrPaoh1qOiprjV
yCVupecFBnPWiIEBCwcuGmihiTYeeOFpkx5DvT+R2suVOnBITpIfnBX7xj2g
tyTHrb7vcastIR7VHOpRJ0MCgzlrxMCAhQMXDbTQRBsPvPD8Gfc+gV5D3XeS
GqQeyE3yhDNj/97FBnRTzB7VrcWtHra6VW1wMGeNGBiwcOCigRaaaOOBF56v
pbfelD5Hz7FJ/VOL1AU5Sr5wduwj9xQu+uEmj/opXib5NgXnrBEDAxYOXDTQ
QhNtPPDCc6j09ePSY13S73Kk95RKH4iVmqQ+yFXyZpScIfvJvbX85fl7tATv
GwxYOHDRQAtNtPHAC88KeaYclv6+UHotfY8eRD+gNqkTcpb84SxvteH5exAD
AxYOXDTQQhNtPPDC0yhfo/bZqLwyqo6M6htG9UmjngtGPQeNeu4b9Z5j1Hud
Ue+xRr63G/k75X//LvsF98IX6w==
"], {{0, 30.}, {30., 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{30., 30.},
PlotRange->{{0, 30.}, {0, 30.}}]\);
normalMap = ResourceFunction["NormalTexture"][heightMap, 3];
heights = ImageData[heightMap];
normals = ImageData[normalMap];
arrows = Table[
point = {j, -i, 4*heights[[i, j]]};
color = RGBColor @@ PixelValue[normalMap, {i, j}];
{color, Arrow[{point, point + 6*(normals[[i, j]] - 0.5)}]}, {i, Length[heights]}, {j, Length[heights[[1]]]}];
Grid[{{Image[normalMap, ImageSize -> 100], Graphics3D[{Arrowheads[0.02], Thick, arrows}, ViewPoint -> {-2.6, -1.23, 1.8}]}}, Spacings -> {2, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/5fc/5fc5ea7f-f287-4d4c-b400-df80515487af/7a3073291d69b06b.png)
|
| Out[34]= |
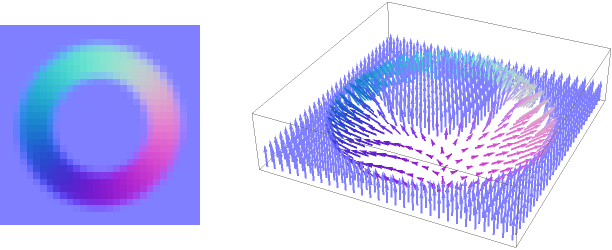
|
This work is licensed under a Creative Commons Attribution 4.0 International License