Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the binormal vector of a curve
ResourceFunction["BinormalVector"][c,t] computes the binormal vector of curve c parametrized by t. |
Consider the curve:
| In[1]:= |
| Out[1]= |  |
The binormal vector:
| In[2]:= |
| Out[2]= |
Use a helix:
| In[3]:= |
The binormal vector:
| In[4]:= |
| Out[4]= |
Calculate the normal vector using the resource function NormalVector:
| In[5]:= |
| Out[5]= |
The normal vector is the cross product of the binormal vector and the tangent vector. Check this using the previous computation along with the resource function TangentVector:
| In[6]:= |
| Out[6]= |
The binormal surface associated to a curve is generated by its binormal vector field. It can be computed with the resource function BinormalSurface:
| In[7]:= |
| Out[7]= |
Check this:
| In[8]:= |
| Out[8]= |
Combine the binormal surface with the helix curve:
| In[9]:= | ![Show[ParametricPlot3D[Evaluate[helix], {t, 0, 2 \[Pi]}, PlotStyle -> Thickness[.02]], ParametricPlot3D[Evaluate[ResourceFunction[
ResourceObject[<|{"Name" -> "BinormalSurface", "ShortName" -> "BinormalSurface", "UUID" -> "b6a1f628-e71e-4a42-9ae0-9497f46a6f3e", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Compute the binormal surface to a curve", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/objects/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$75f48fc0f00241ddbf1fc27dbaca5316`BinormalSurface", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/322e6a95-f4b3-4dee-a881-205415c7cc7c"]}|>, ResourceSystemBase -> "https://www.wolframcloud.com/objects/resourcesystem/api/1.0"]][helix, t, {u, v}]], {u, 0, 2 \[Pi]}, {v, 0, 5}, PlotPoints -> {20, 10}]]](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56ffcc31-24bb-4b98-b17d-cacb7f775a3f/3d7895d20b9b4f25.png) |
| Out[9]= | 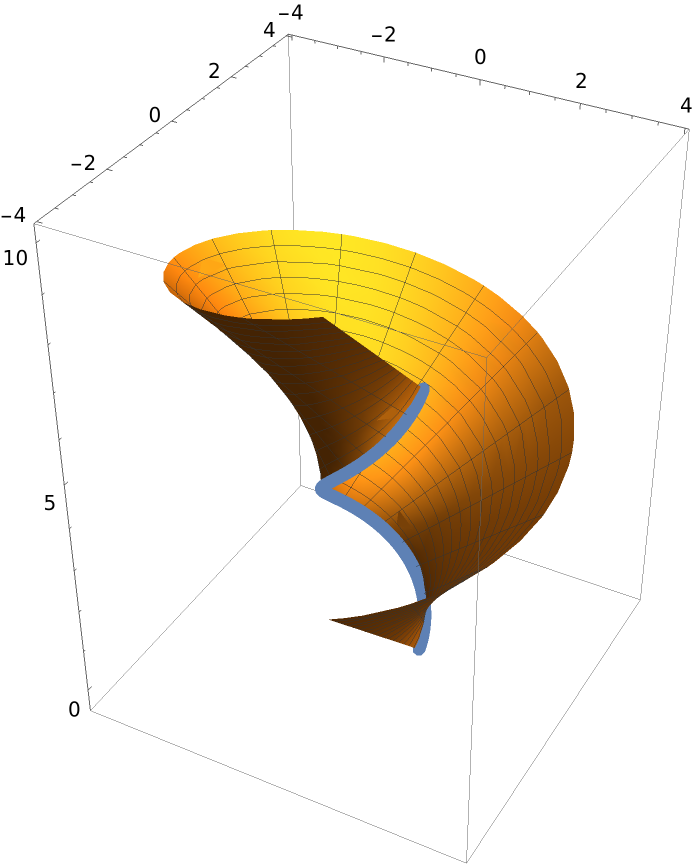 |
Define a unit speed helix:
| In[10]:= | ![uhelix = {a Cos[t/Sqrt[a^2 + b^2]], a Sin[t/Sqrt[a^2 + b^2]], (b t)/
Sqrt[a^2 + b^2]};](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56ffcc31-24bb-4b98-b17d-cacb7f775a3f/178af3743405cf7e.png) |
Its binormal vector:
| In[11]:= |
| Out[11]= | 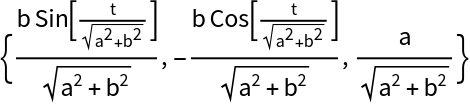 |
The derivative of the binormal vector:
| In[12]:= |
| Out[12]= |
The torsion, via the resource function CurveTorsion:
| In[13]:= |
| Out[13]= |
The normal vector, via the resource function NormalVector:
| In[14]:= |
| Out[14]= |
The torsion multiplied by the normal is the derivative of the binormal:
| In[15]:= |
| Out[15]= |
Using FrenetSerretSystem, the binormal vector is the last element of the second List:
| In[16]:= |
| Out[16]= | 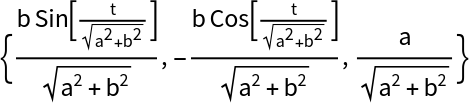 |
This work is licensed under a Creative Commons Attribution 4.0 International License