Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the parametrization of a tube of variable section
ResourceFunction["VariableSectionTube"][c,r,{t,θ}] computes the parametrization of a tube from a curve c and of variable section radius r with respect to variables t and θ. |
Create tubes from a circle:
| In[1]:= |
| Out[1]= |
Plot them:
| In[2]:= | ![ParametricPlot3D[
Evaluate[
ResourceFunction[
"VariableSectionTube"][{ Cos[t], Sin[t], 0}, #, {t, \[Theta]}]], {t, 0, 2 \[Pi]}, {\[Theta], 0, 2 \[Pi]}] & /@ {1 + Cos[t], .5 + .2 Cos[t], .2 + .5 Cos[t]}](https://www.wolframcloud.com/obj/resourcesystem/images/2e0/2e039e50-f704-41b8-b422-bec534477dfe/2abc542840597720.png) |
| Out[2]= | 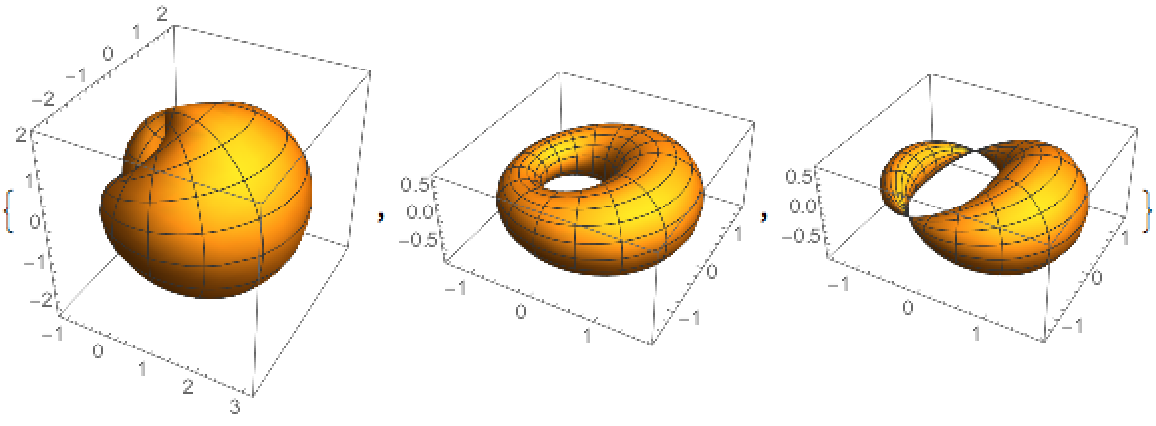 |
Create tubes based on a Sin function with angular frequency 4:
| In[3]:= | ![ParametricPlot3D[
Evaluate[
ResourceFunction["VariableSectionTube"][5 { Cos[t], Sin[t], 0}, 1.5 + 0.75 Sin[4 t], {t, \[Theta]}]], {t, 0, 4 \[Pi]}, {\[Theta], 0, 2 \[Pi]}, PlotPoints -> {40, 15}]](https://www.wolframcloud.com/obj/resourcesystem/images/2e0/2e039e50-f704-41b8-b422-bec534477dfe/7513416bbc698fb6.png) |
| Out[3]= | 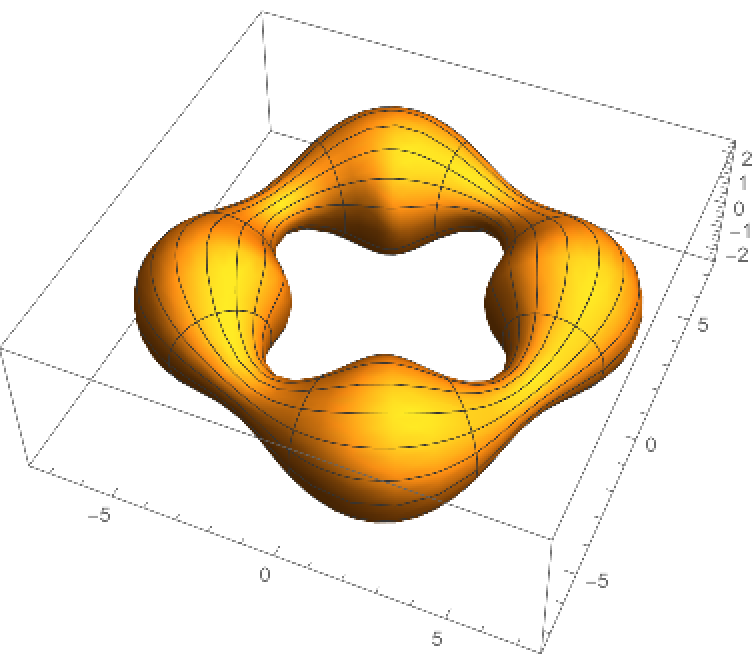 |
Create a tube from a helix:
| In[4]:= |
| In[5]:= | ![ParametricPlot3D[
Evaluate[
ResourceFunction["VariableSectionTube"][
helix[1, 2.5, 2.2][t], .2 t + .2 Sin[2 t], {t, \[Theta]}]], {t, 0, 6 \[Pi]}, {\[Theta], 0, 2 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/2e0/2e039e50-f704-41b8-b422-bec534477dfe/32777e8d2c1b8330.png) |
| Out[5]= | 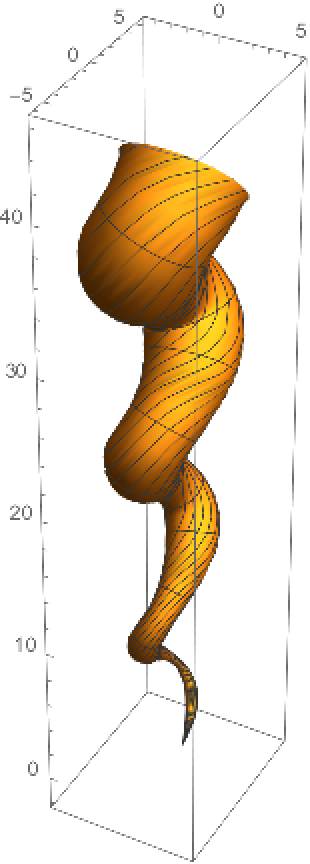 |
This work is licensed under a Creative Commons Attribution 4.0 International License