Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
Vertical Transmission Models |  |
returns an expanded list of transitions tr i bc i r i | |
returns an expanded list of transitions tr i bc i sc ij r i |
VitalDemographicsModel |
CompartmentalModelGraph |
options |
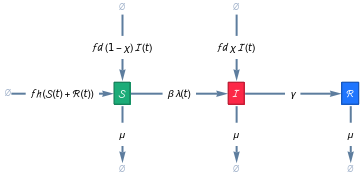
VitalDemographicsModel |
CompartmentalModelGraph |
options |

returns an association of model data for the input transitions in tr i t |
"BirthCompartments" | a list rules { bc i r i { bc i sc ij r i bc i sc ij r i |
"AgeStratification" | a list {symb,n} symb n |
"AgeStratifiedParameters" | a list of parameters to stratify by age along with the compartments; integers are used for the indices |
DynamicTransmissionModel |
CompartmentalModelGraph |
options |
wrap edge labels |
