Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Struve–Kelvin stei function
ResourceFunction["StruveKelvinStei"][z] gives the Struve–Kelvin function stei(z). | |
ResourceFunction["StruveKelvinStei"][n,z] gives the Struve–Kelvin function stein(z). |
Evaluate numerically:
| In[1]:= |
| Out[1]= |
Plot stei(x):
| In[2]:= |
| Out[2]= |  |
Evaluate for complex arguments and orders:
| In[3]:= |
| Out[3]= |
Evaluate to high precision:
| In[4]:= |
| Out[4]= |
The precision of the output tracks the precision of the input:
| In[5]:= |
| Out[5]= |
StruveKelvinStei threads elementwise over lists:
| In[6]:= |
| Out[6]= |
Use FunctionExpand to expand Struve–Kelvin functions of half-integer orders:
| In[7]:= |
| Out[7]= | 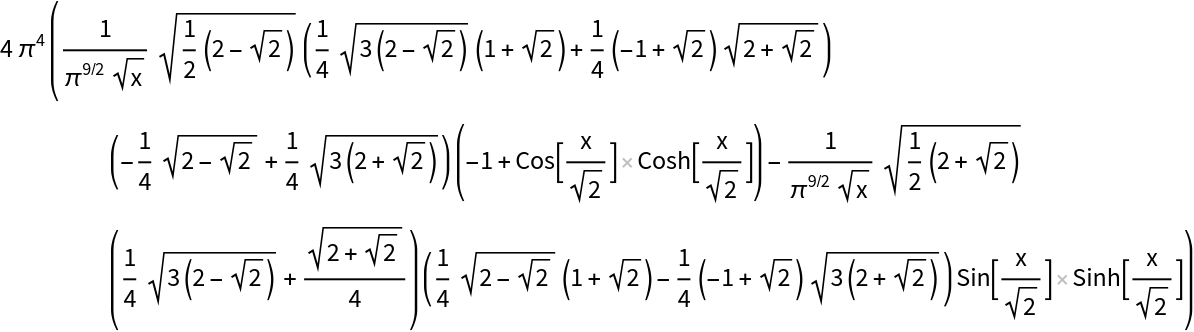 |
This work is licensed under a Creative Commons Attribution 4.0 International License