Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a Mercer matrix
ResourceFunction["MercerMatrix"][n] returns the n×n Mercer matrix. |
A 4×4 Mercer matrix:
| In[1]:= |
| Out[1]= |
Its 4th power is the zero matrix:
| In[2]:= |
| Out[2]= |
Visualize the entries of a Mercer matrix:
| In[3]:= |
| Out[3]= |  |
By default, an exact matrix is computed:
| In[4]:= |
| Out[4]= |  |
Use machine precision:
| In[5]:= |
| Out[5]= |  |
Use arbitrary precision:
| In[6]:= |
| Out[6]= |  |
The nth matrix power of an n×n Mercer matrix is the zero matrix; that is, the Mercer matrix is nilpotent (and thus, singular as well):
| In[7]:= |
| Out[7]= |
The Drazin inverse of an n×n Mercer matrix is the zero matrix:
| In[8]:= |
| Out[8]= |
The only null vector (which is also the only eigenvector) of the Mercer matrix has a simple form:
| In[9]:= |
| Out[9]= |
Show that all entries are non-zero for each power of the Mercer matrix until the nth:
| In[10]:= |
| Out[10]= | 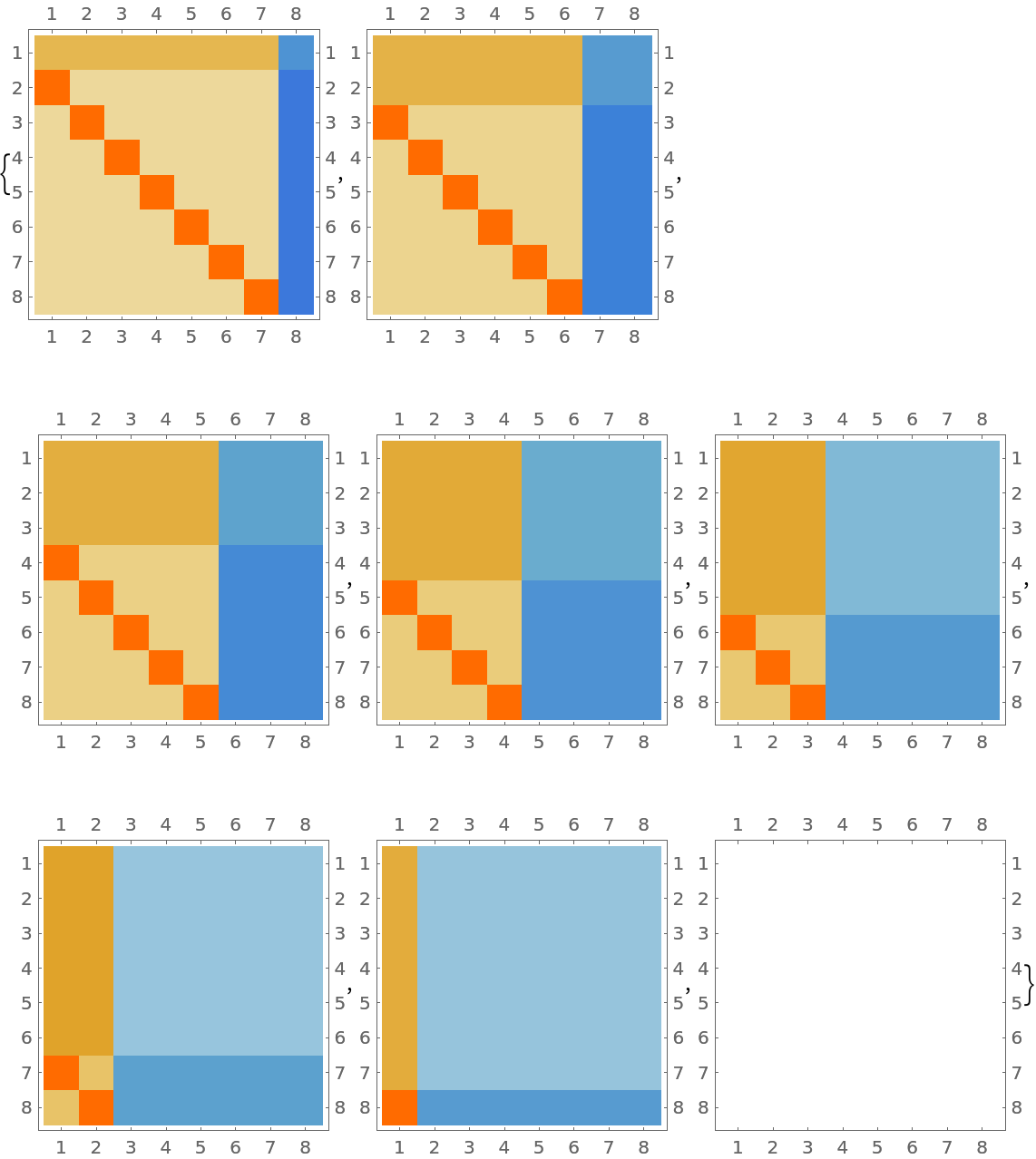 |
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License