Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a matrix that arises in the computation of the discrete Hilbert transform
ResourceFunction["DiscreteHilbertTransformMatrix"][n] returns an n×n Hilbert transform matrix. |
A 4×4 Hilbert transform matrix:
| In[1]:= |
| Out[1]= | 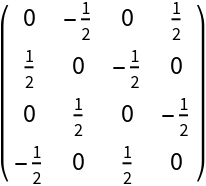 |
Visualize a Hilbert transform matrix of odd dimension:
| In[2]:= |
| Out[2]= | 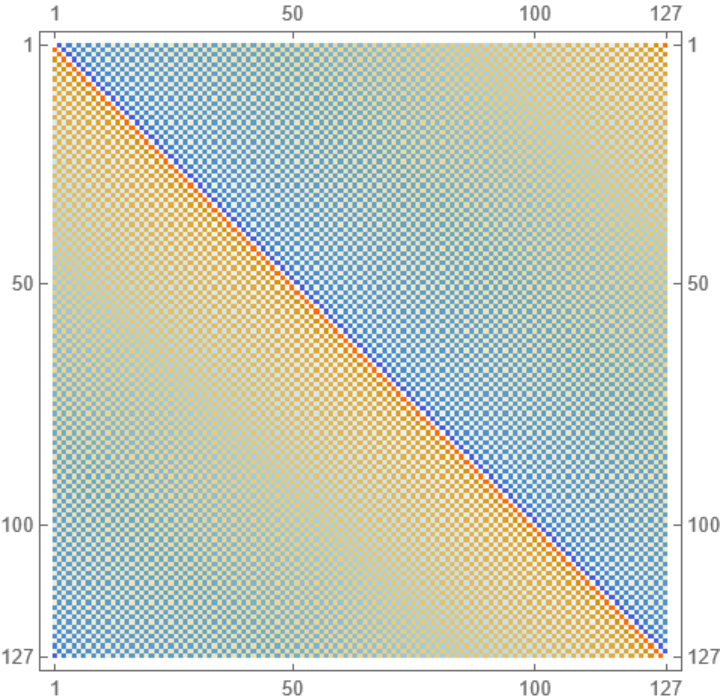 |
By default, an exact matrix is computed:
| In[3]:= |
| Out[3]= | 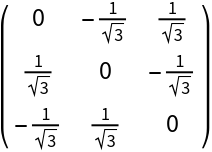 |
Use machine precision:
| In[4]:= |
| Out[4]= |
Use arbitrary precision:
| In[5]:= |
| Out[5]= |
The Hilbert transform matrix is antisymmetric:
| In[6]:= |
| Out[6]= | 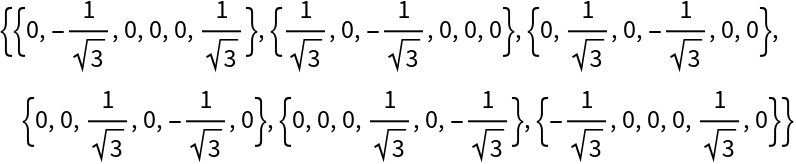 |
| In[7]:= |
| Out[7]= |
Compute the discrete Hilbert transform of a vector by multiplying it with the Hilbert transform matrix:
| In[8]:= |
| In[9]:= |
| Out[9]= |
Using the resource function DiscreteHilbertTransform is faster:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License