Function Repository Resource:

WiggleLine

Make a line that wiggles

Contributed by: Nik Murzin

ResourceFunction["WiggleLine"][points]

creates a Line that wiggles along a smoothed BSplineCurve derived from the given list of points.

ResourceFunction["WiggleLine"][f]

wiggles along the curve given by f.

Details and Options

Curves supported by f include BSplineFunction, BezierFunction and InterpolatingFunction expressions.

ResourceFunction["WiggleLine"] supports the following options:

"Shape"

"Sine"

wiggle shape function or one of "Sine", "Square", "Triangle", "Sawtooth", "Helix", "Semicircles", "Braid"

"Frequency"

frequency of the wiggle

"Amplitude"

amplitude of the wiggle

"TaperFraction"

fraction of a line to taper off near the endpoints

"Points"

number of line points

"Semicircles" and "Braid" shapes consist of Circle segments.

Examples

Basic Examples (2)

Make a wiggly line between two points:

In[1]:=

Out[1]=

Make a curvier wiggly line:

In[2]:=

Out[2]=

Scope (1)

Use BSplineFunction, BezierFunction or InterpolatingFunction as input:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

In[5]:=

Out[5]=

Options (7)

Frequency (1)

Change the wiggle frequency:

In[6]:=

Out[6]=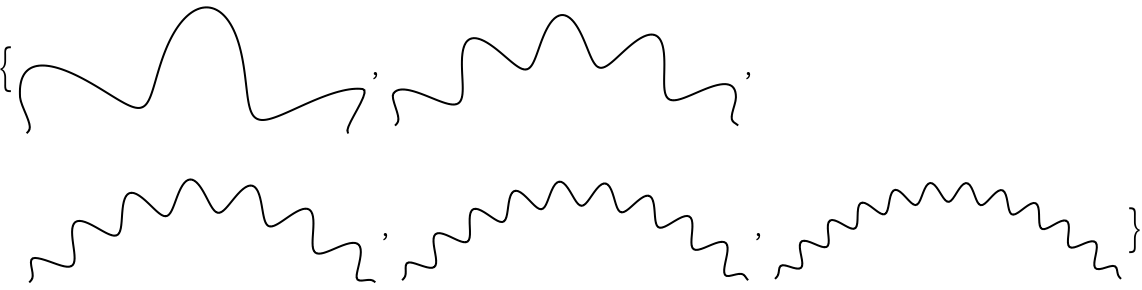

Amplitude (1)

Change the wiggle amplitude:

In[7]:=

Out[7]=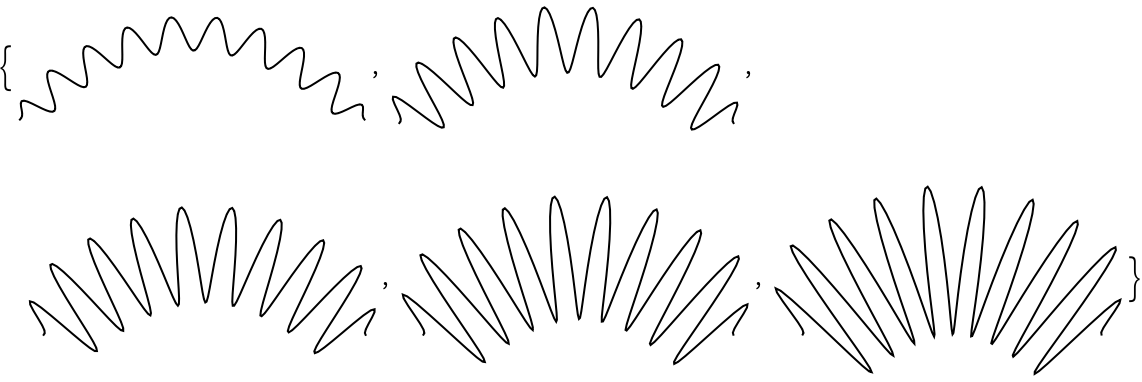

TaperFraction (2)

Change the amount of taper at endpoints:

In[8]:=

Out[8]=

No taper may produce a wiggle that misses its specified endpoints:

In[9]:=

Out[9]=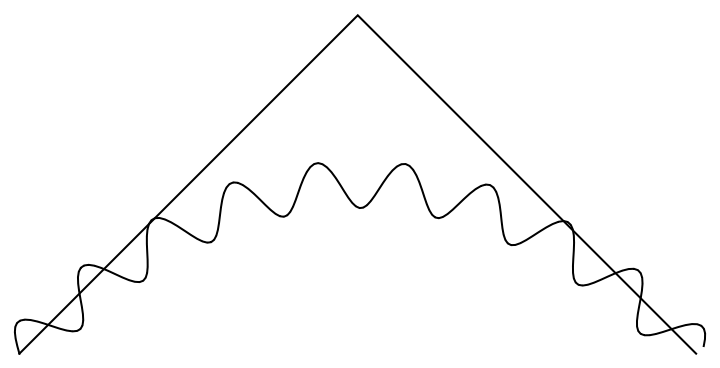

Shape (2)

There are number of built-in wiggly shapes:

In[10]:=

With[{pts = {{0, 0}, {1, 1}, {2, 0}}},
GraphicsGrid@
Partition[
Graphics[{ResourceFunction["WiggleLine"][pts, "Shape" -> #]}, PlotLabel -> #] & /@ {"Sine", "Square", "Triangle", "Sawtooth", "Helix", "Semicircles", "Braid"}, UpTo[3]]
]

Out[10]=

Use custom function as a shape:

In[11]:=

Out[11]=

Points (1)

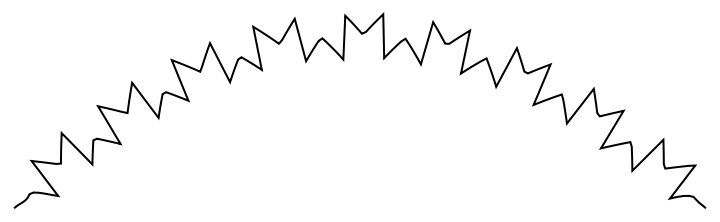Provide the exact number of line points to return:

In[12]:=

Out[12]=

Applications (1)

Draw a Feynman Diagram:

In[13]:=

Graphics[{
Arrowheads[{{Medium, .5}}], Arrow[{{0, 1}, {1, 0}}], Arrow[{{1, 0}, {0, -1}}],
Arrow[{{2, .2}, {3, 1}}], Arrow[{{3, -1}, {2, .2}}],
Arrowheads[{{Small, .556, Graphics[Line[{{{-1, 1/2}, {0, 0}, {-1, -1/2}}}]]}}],
Arrow@ResourceFunction["WiggleLine"][{{1, 0}, {2, .2}}, "Shape" -> "Helix", "Amplitude" -> .03]
}]

Out[13]=

Possible Issues (1)

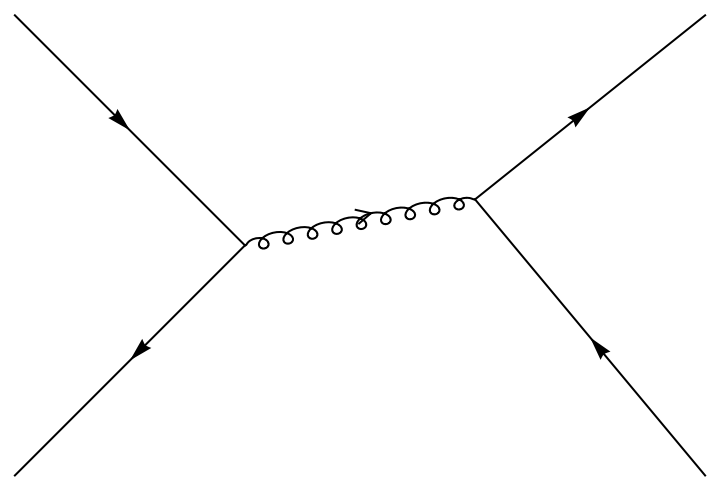If length of the line is too small, WiggleLine returns a single Point:

In[14]:=

$ResourceFunction["WiggleLine"][{{0, 0}, {1*^-13, 0}}]$

Out[14]=

Neat Examples (1)

Wiggle some fractal curves:

In[15]:=

Out[15]=

In[16]:=

Out[16]=

In[17]:=

Out[17]=

In[18]:=

Out[18]=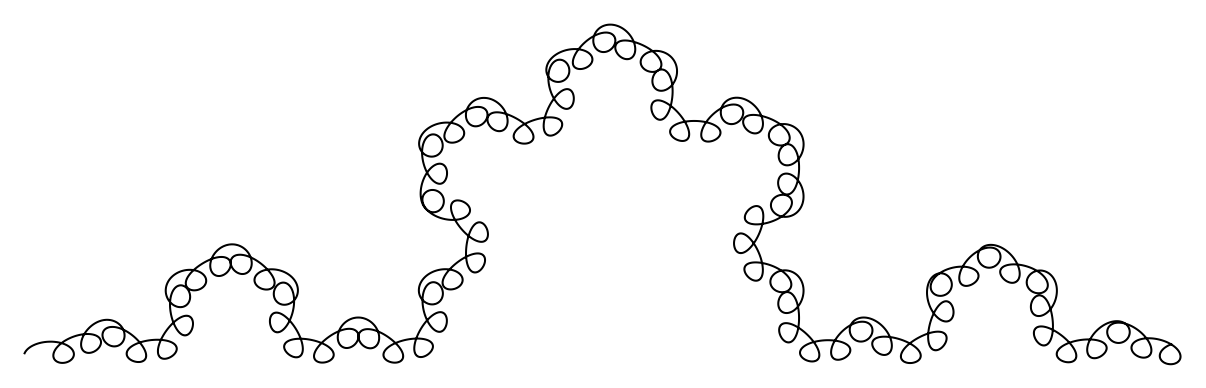

In[19]:=

Out[19]=

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

1.0.0 – 04 April 2025

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License