Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RicciCurvature

Source Notebook

Compute the components of the Ricci curvature for a metric

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["RicciCurvature"][m,{u,v}]

computes the components of the Ricci curvature for a metric.

Details and Options

The Ricci curvature quantifies the local deviation of the geometry of a metric tensor from ordinary Euclidean space.

Examples

Basic Examples (5) 

The monkey saddle surface:

In[1]:=
monkeysaddle[u_, v_] := {u, v, u^3 - 3 u v^2}
In[2]:=
ms = monkeysaddle[u, v]
Out[2]=

Plot the surface:

In[3]:=
ParametricPlot3D[{u, v, u^3 - 3 u v^2}, {u, -\[Pi], \[Pi]}, {v, -\[Pi], \[Pi]}, BoxRatios -> {1, 1, 1}, PlotRange -> All]
Out[3]=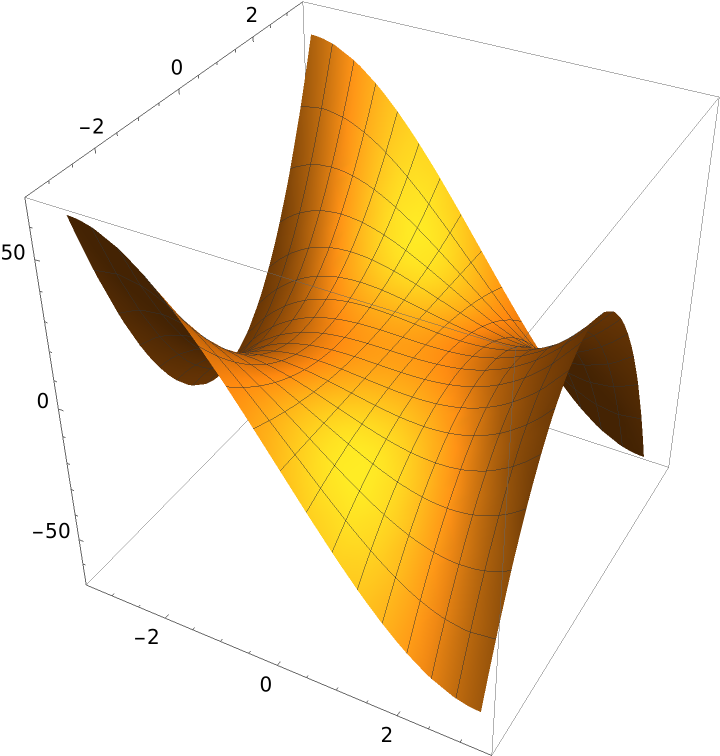

The covariant basis:

In[4]:=
{Subscript[g, \[Alpha]], Subscript[g, \[Beta]]} = Transpose@(D[{u, v, u^3 - 3 u v^2}, {{u, v}}])
Out[4]=

The metric tensor:

In[5]:=
Subscript[g, \[Alpha]\[Beta]] = SymmetrizedArray[{{1, 1} -> Subscript[g, \[Alpha]] . Subscript[g, \[Alpha]], {1, 2} -> Subscript[g, \[Alpha]] . Subscript[g, \[Beta]], {2, 2} -> Subscript[g, \[Beta]] . Subscript[g, \[Beta]]}, {2, 2}, Symmetric[{1, 2}]] // Simplify
Out[5]=

The Ricci curvature:

In[6]:=
ResourceFunction["RicciCurvature"][Subscript[ g, \[Alpha]\[Beta]], {u, v}] // FullSimplify
Out[6]=

Properties and Relations (2) 

Alternatively, Ricci curvature can be computed contracting an index of the Riemann tensor. Compute the same tensor as above:

In[7]:=
{Subscript[g, \[Alpha]], Subscript[g, \[Beta]]} = Transpose@(D[{u, v, u^3 - 3 u v^2}, {{u, v}}])
Out[7]=
In[8]:=
Subscript[g, \[Alpha]\[Beta]] = SymmetrizedArray[{{1, 1} -> Subscript[g, \[Alpha]] . Subscript[g, \[Alpha]], {1, 2} -> Subscript[g, \[Alpha]] . Subscript[g, \[Beta]], {2, 2} -> Subscript[g, \[Beta]] . Subscript[g, \[Beta]]}, {2, 2}, Symmetric[{1, 2}]] // Simplify
Out[8]=

The same result is found using the resource functions ArrayContract and RiemannTensor:

In[9]:=
rc = ResourceFunction["ArrayContract"][ ResourceFunction["RiemannTensor"][Subscript[ g, \[Alpha]\[Beta]], {u, v}], {{1, 3}}] // FullSimplify
Out[9]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 29 October 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.
    • Loveridge, L. C., "Physical and Geometric Interpretations of the Riemann Tensor, Ricci Tensor, and Scalar Curvature." arXiv Preprint, 2004. https://arxiv.org/abs/gr-qc/0401099

Related Resources

License Information