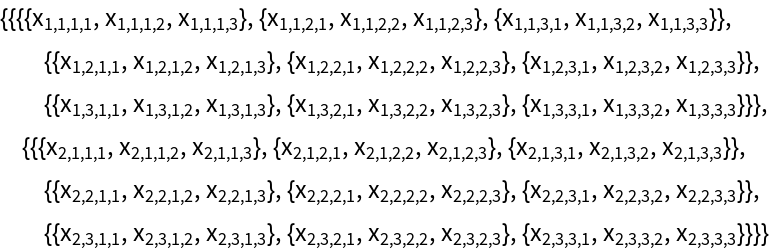Function Repository Resource:

ArrayContract

Source Notebook

General contraction of levels of an array

Contributed by: Jose Martin-Garcia

ResourceFunction["ArrayContract"][a,{{l₁,…,l_n}}]

contracts levels l₁, …, l_n of the array a using head Plus.

ResourceFunction["ArrayContract"][a,{ctr₁,ctr₂,…}]

performs several contractions in the array a.

ResourceFunction["ArrayContract"][a,ctrs,g]

performs contractions ctrs using head g.

ResourceFunction["ArrayContract"][a,ctrs,g,d]

performs contractions assuming that only the first d levels of the array a are array levels.

Details and Options

Each contraction ctr_i in the contraction list must be a list of positive integers from 1 to the depth of the array. Levels cannot be repeated, neither in a given contraction nor in different contractions.

For each contraction ctr_i in the contraction list, all levels must have the same array dimension.

The array a must be rectangular up to the deepest level involved in the contractions.

The effective depth d in ResourceFunction["ArrayContract"][a,ctrs,g,d] can be used to indicate that array a should be treated as if it had only d levels. Therefore, d must be an integer between 0 and the array depth of a, and all contraction levels must be between 1 and d. By default, d is chosen to be the depth of the array a.

Examples

Basic Examples (4)

Take an array of depth 4:

In[1]:=

Out[1]=

Contract levels 2 and 3:

In[2]:=

Out[2]=

Contract levels 2, 3 and 4:

In[3]:=

Out[3]=

Use head g for the contraction:

In[4]:=

Out[4]=

Scope (8)

Use arrays of any depth:

In[5]:=

Out[5]=

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Perform contractions of any number of levels:

In[8]:=

Out[8]=

In[9]:=

Out[9]=

In[10]:=

Out[10]=

In[11]:=

Out[11]=

In[12]:=

Out[12]=

In[13]:=

Out[13]=

Perform any number of contractions simultaneously:

In[14]:=

In[15]:=

Out[15]=

In[16]:=

Out[16]=

Use any head for contractions:

In[17]:=

In[18]:=

Out[18]=

In[19]:=

Out[19]=

Heads with attribute Flat, like Plus, will then combine, eliminating nesting:

In[20]:=

Out[20]=

Take an array of depth 4:

In[21]:=

Contract levels 1 and 3 into a single level with head g, which by default is placed where level 3 was, effectively considering that the original array had depth 3:

In[22]:=

Out[22]=

In[23]:=

Out[23]=

Move the contracted level one level deeper:

In[24]:=

Out[24]=

Listable heads automatically move as deep as possible in the array, ignoring the effective depth argument:

In[25]:=

Out[25]=

In[26]:=

Out[26]=

In[27]:=

Out[27]=

Arrays must be rectangular, at least up to the level given by the effective depth:

In[28]:=

In[29]:=

Out[29]=

In[30]:=

Out[30]=

In[31]:=

Out[31]=

As a corner case, effective depth 0 is possible when there are no contractions:

In[32]:=

In[33]:=

Out[33]=

Contract sparse arrays, quantity arrays or other types of structured arrays:

In[34]:=

Out[34]=

In[35]:=

Out[35]=

Properties and Relations (7)

Tr can contract only the higher levels of an array:

In[36]:=

Out[36]=

In[37]:=

Out[37]=

ArrayContract can contract any group of levels:

In[38]:=

Out[38]=

Performing this operation with Tr would require transpositions:

In[39]:=

Out[39]=

Empty contractions are ignored:

In[40]:=

In[41]:=

Out[41]=

In[42]:=

Out[42]=

The presence of a contraction head is irrelevant if all contractions are empty:

In[43]:=

Out[43]=

TensorContract and ArrayContract can both perform several contractions:

In[44]:=

In[45]:=

Out[45]=

TensorContract always uses Plus as a contraction head, but ArrayContract can use any head:

In[46]:=

Out[46]=

TensorContract can handle symbolic expressions, but ArrayContract only acts on explicit arrays:

In[47]:=

$TensorContract[ IdentityMatrix[d]\[TensorProduct]IdentityMatrix[d], {{2, 3}}] // TensorDimensions$

Out[47]=

In[48]:=

$ResourceFunction["ArrayContract"][ IdentityMatrix[4]\[TensorProduct]IdentityMatrix[4], {{2, 3}}] // Dimensions$

Out[48]=

ArrayContract can perform transpositions, using effectively the same notation as Flatten:

In[49]:=

In[50]:=

Out[50]=

ArrayContract generalizes Apply on consecutive levels, with levels shifted by one:

In[51]:=

In[52]:=

Out[52]=

In[53]:=

Out[53]=

Transpose can also perform simultaneous contractions with head List:

In[54]:=

In[55]:=

Out[55]=

In[56]:=

Out[56]=

The order of contractions is relevant:

In[57]:=

Out[57]=

In[58]:=

Out[58]=

In[59]:=

Out[59]=

In[60]:=

Out[60]=

In[61]:=

Out[61]=

In[62]:=

Out[62]=

Publisher

Jose Martin-Garcia

Version History

1.0.0 – 05 August 2020

Related Resources

Author Notes

• This function is rather slow, and normalizes everything. It is essentially a prototype to explore the generality of the possible concept.

• This function could still be generalized: 1) The third argument could take a list of heads, one per contraction. Right now all contractions in the second argument use the same head in the third argument. This will be implemented in 12.2. 2) Like Tr, it should be possible to contract to the lowest dimension, instead of requiring coinciding dimensions. 3) The levels in the contraction could be processed with some other function (say Flatten instead of Tr), as long as the result produces a single level again. This is probably a separate function.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License