Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct a specified Kimberling center of a triangle
ResourceFunction["KimberlingCenter"][tri,n] returns the nth Kimberling triangle center of a triangle tri. |
| X1 | 1 | incenter I |
| X2 | 2 | centroid G |
| X3 | 3 | circumcenter O |
| X4 | 4 | orthocenter H |
| X5 | 5 | nine-point center N |
| X6 | 6 | symmedian K |
| X7 | 7 | Gergonne Ge |
| X8 | 8 | Nagel Na |
| X9 | 9 | mittenpunkt M |
| X10 | 10 | Spieker Sp |
| X11 | 11 | Feuerbach F |
| X13 | 13 | Fermat X |
Find the incenter, X1 or I, where the angle bisectors intersect:
| In[1]:= |
| Out[2]= |
Show it:
| In[3]:= |
| Out[3]= | 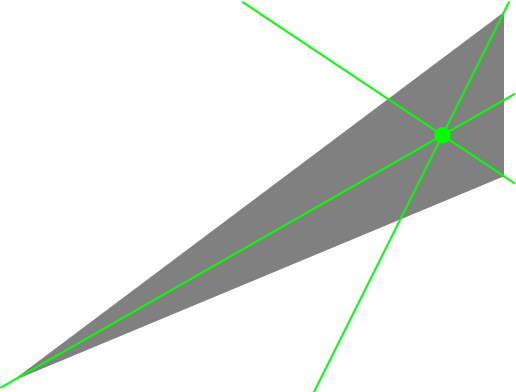 |
Find the centroid, X2 or G, where the angle medians intersect:
| In[4]:= |
| Out[5]= |
Show it:
| In[6]:= | ![Graphics[{Gray, Triangle[tri], Green, InfiniteLine[{x2, Mean[#]}] & /@ Subsets[tri, {2}], Red, Disk[x2, .2]}]](https://www.wolframcloud.com/obj/resourcesystem/images/eca/ecacd7c0-1f46-443d-ac7e-01bc3e9a1701/67528ee0023edda7.png) |
| Out[6]= | 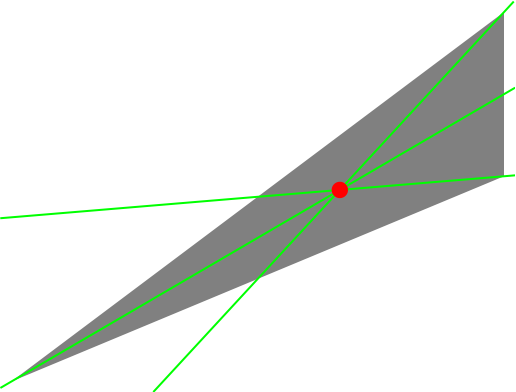 |
This is equivalent to the result of TriangleCenter or Mean:
| In[7]:= | ![{
ResourceFunction["KimberlingCenter"][tri, 2],
TriangleCenter[tri, "Centroid"],
Mean[tri]}](https://www.wolframcloud.com/obj/resourcesystem/images/eca/ecacd7c0-1f46-443d-ac7e-01bc3e9a1701/154db483e1325690.png) |
| Out[8]= |
Find the circumcenter, X3 or O, where the perpendicular bisectors intersect:
| In[9]:= |
| Out[10]= |
Show it:
| In[11]:= | ![Graphics[{Gray, Triangle[tri], Green, InfiniteLine[{x3, Mean[#]}] & /@ Subsets[tri, {2}], Red, Disk[x3, .2]}]](https://www.wolframcloud.com/obj/resourcesystem/images/eca/ecacd7c0-1f46-443d-ac7e-01bc3e9a1701/3a193245a794f5b1.png) |
| Out[11]= | 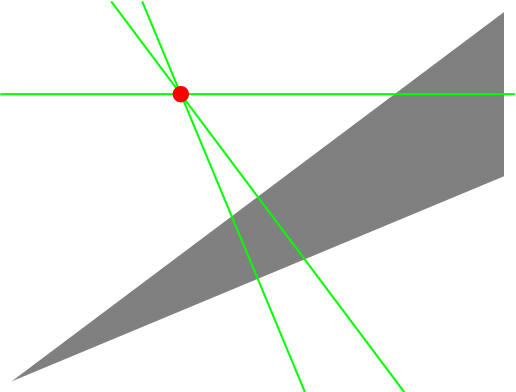 |
Equivalent ways to compute the circumcenter:
| In[12]:= | ![x3 = {
ResourceFunction["KimberlingCenter"][tri, 3],
TriangleCenter[tri, "Circumcenter"],
Circumsphere[tri]}](https://www.wolframcloud.com/obj/resourcesystem/images/eca/ecacd7c0-1f46-443d-ac7e-01bc3e9a1701/60fbccacfa51de75.png) |
| Out[13]= |
Find the orthocenter, X4 or H, where the altitudes intersect:
| In[14]:= |
| Out[15]= |
Show it:
| In[16]:= | ![Graphics[{Gray, Triangle[tri], Green, InfiniteLine[{x4, #}] & /@ tri, Black, InfiniteLine@# & /@ Subsets[tri, {2}], Red, Disk[x4, .2]}]](https://www.wolframcloud.com/obj/resourcesystem/images/eca/ecacd7c0-1f46-443d-ac7e-01bc3e9a1701/6b70a289a7719dd3.png) |
| Out[16]= | 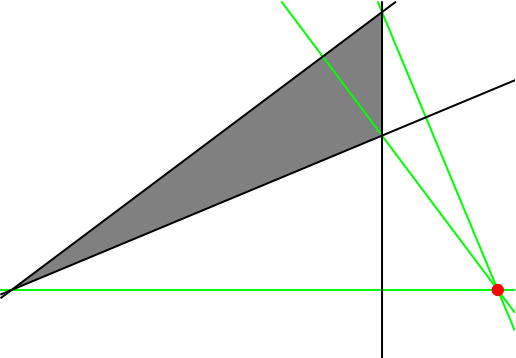 |
Equivalent ways to compute the orthocenter:
| In[17]:= | ![{
ResourceFunction["KimberlingCenter"][tri, 4],
TriangleCenter[tri, "Orthocenter"],
ResourceFunction["Orthocenter"][tri]}](https://www.wolframcloud.com/obj/resourcesystem/images/eca/ecacd7c0-1f46-443d-ac7e-01bc3e9a1701/00bd2a91ceca3394.png) |
| Out[17]= |
Find the Spieker point X10 of a triangle:
| In[18]:= |
| Out[18]= |
The Euler infinity point, X30, is not currently supported by KimberlingCenter. Find and show the first 29 Kimberling centers:
| In[19]:= | ![tri = {{0, 0}, {-3, 1}, {3, 4}};
Graphics[{EdgeForm[Black], White, Polygon[tri], Black, Table[Text[n, ResourceFunction["KimberlingCenter"][tri, n]], {n, 1, 29}]}, PlotRange -> {{-4, 7}, {-4, 7}}]](https://www.wolframcloud.com/obj/resourcesystem/images/eca/ecacd7c0-1f46-443d-ac7e-01bc3e9a1701/4e414d965bf082f1.png) |
| Out[20]= | 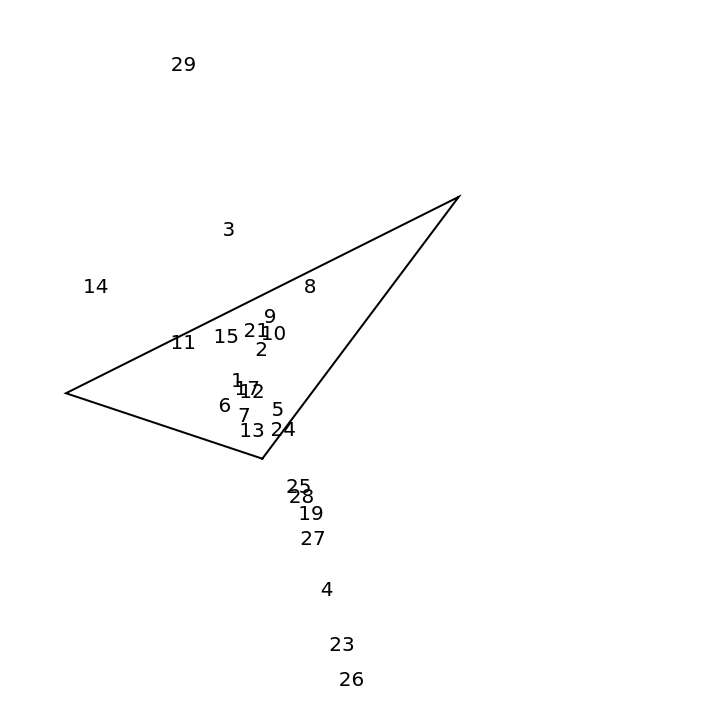 |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License