Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DysonTerms

Source Notebook

Generate the nth term in the Dyson series of a time-dependent operator

Contributed by: Bruno Tenorio

ResourceFunction["DysonTerms"][op,n]

generates the order-n term in the Dyson series of the operator op.

ResourceFunction["DysonTerms"][op,n,alg]

uses operation alg instead of NonCommutativeMultiply.

ResourceFunction["DysonTerms"][op,n, alg, t0]

uses t0 instead of 0 as the initial integration time.

Details and Options

The Dyson series expresses the time evolution operator 𝒰(t, t0) for a time-dependent Hamiltonian H(t) as a time ordered exponential: 
𝒰(t,t0) = 𝒯 exp(- )
ResourceFunction["DysonTerms"] returns the n-th order term in the series expansion as . This construct enforces the time ordering (t >= t1>= t2…tn>=t0). Here we assume ℏ = 1.
This is useful for perturbative calculations in quantum mechanics, time-dependent perturbation theory, and quantum field theory.
ResourceFunction["DysonTerms"] takes the following option:
"NumericIntegration"FalseIf set as True, it will return a function in terms of NIntegrate where the parameter is the upper limit. Otherwise it will do symbolic integration.

Examples

Basic Examples (3) 

First order term D1:

In[1]:=
ResourceFunction["DysonTerms"][\[FormalCapitalA], 1]
Out[1]=

Second order term D2:

In[2]:=
ResourceFunction["DysonTerms"][\[FormalCapitalA], 2]
Out[2]=

Second order term with Dot operation:

In[3]:=
ResourceFunction["DysonTerms"][\[FormalCapitalB], 2, Dot]
Out[3]=

Third order term D3, with lower integration limit equal to 1:

In[4]:=
ResourceFunction["DysonTerms"][\[FormalCapitalB], 3, 1]
Out[4]=

Scope (3) 

Dyson series up to third order for some generic operator in 2×2 Pauli algebra:

In[5]:=
Sum[ResourceFunction["DysonTerms"][\[FormalCapitalA], j, {Dot, 2}], {j, 0, 3}]
Out[5]=

Get the second order Dyson term for the particular time dependent operator Δ/2 σz + A Cos(ω t) σx:

In[6]:=
ClearAll[h4, \[CapitalDelta], \[Omega], A, \[Sigma]] h4[t_] := \[CapitalDelta]/2 PauliMatrix[3] + A Cos[\[Omega] t] PauliMatrix[1]; ResourceFunction["DysonTerms"][h4, 2, Dot]
Out[8]=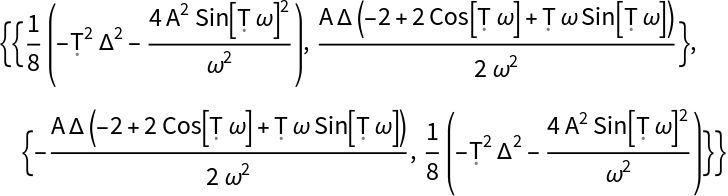

Consider a time dependent operator for fermionic algebra , where α and β are time dependent complex valued functions:

In[9]:=
V[t_] := \[Alpha][t] c + \[Beta][t] SuperDagger[c]

Define the algebra:

In[10]:=
alg = NonCommutativeAlgebra[<| "ScalarVariables" -> Join[Flatten@ Outer[#2[#1] &, {Subscript[\[FormalT], 1], Subscript[\[FormalT], 2]}, {Identity, \[Alpha], \[Beta]}], {\[FormalCapitalT]}]|>];

Function for reducing fermionic algebra {c,c†}=1, {c,c} = 0, {c†,c†} = 0:

In[11]:=
reducer = NonCommutativePolynomialReduce[#, {Anticommutator[c, SuperDagger[ c]] - 1, c ** c, SuperDagger[c] ** SuperDagger[c]}, {c, SuperDagger[c]}, alg] &;

Consider the full Dyson series up to the second order:

In[12]:=
series = Sum[ResourceFunction["DysonTerms"][V, j, alg], {j, 0, 2}]
Out[12]=

Normal order the terms; the integrals will depend on the scalar functions α and β:

In[13]:=
series /. Integrate[integrand_, rest___] :> Integrate[reducer[integrand][[-1]], rest]
Out[13]=

Options (4) 

Define an operator in Pauli algebra:

In[14]:=
ClearAll[h1]; h1[t_] := Exp[-t^2] Cos[2 t] PauliMatrix[2] + Sin[2 t] PauliMatrix[3]

For a second order term an exact expression could not be obtained or takes too long to integrate:

In[15]:=
TimeConstrained[ResourceFunction["DysonTerms"][h1, 2, Dot], 20]
Out[15]=

Get a function to do numeric integration:

In[16]:=
num = ResourceFunction["DysonTerms"][h1, 2, Dot, "NumericIntegration" -> True];

Evaluate at some particular final time:

In[17]:=
num[6.]
Out[17]=

Applications (17) 

Driving field (4) 

Time dependent drive: VI(t) = g (ⅇⅈ ω t a + ⅇ-ⅈ ω t a†) for bosonic algebra:

In[18]:=
Vi[t_] := g ( E^(I \[Omega] t) \[FormalA] + E^(-I \[Omega] t) SuperDagger[\[FormalA]])

Define the algebra and a reduction function:

In[19]:=
alg = NonCommutativeAlgebra[<| "ScalarVariables" -> {h, g, \[Omega], Subscript[\[FormalT], 1], Subscript[\[FormalT], 2], \[FormalCapitalT]}|>]; reducer = NonCommutativePolynomialReduce[#, {\[FormalA] ** SuperDagger[\[FormalA]] - SuperDagger[\[FormalA]] ** \[FormalA] - 1}, {\[FormalA], SuperDagger[\[FormalA]]}, alg] &;

First order term:

In[20]:=
ResourceFunction["DysonTerms"][Vi, 1, alg]
Out[20]=

Second order term, simplified in normal order form:

In[21]:=
reducer[ResourceFunction["DysonTerms"][Vi, 2, alg]][[-1]]
Out[21]=

Chirped Gaussian Pulse (13) 

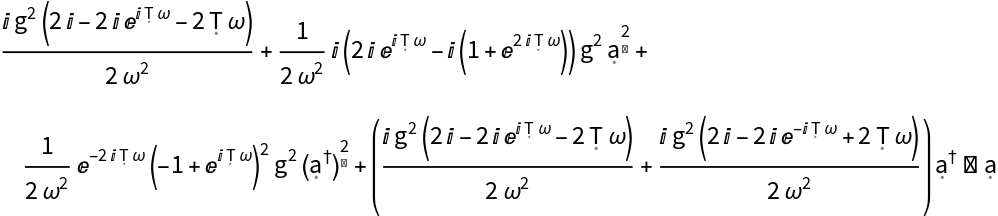In[22]:=
ClearAll[\[CapitalOmega]0, \[Tau], \[Kappa]] Hchirped[t_] := 1/2 \[CapitalOmega]0 E^(-t^2 / \[Tau]^2) (Cos[\[Kappa] t^2] PauliMatrix[1] + Sin[\[Kappa] t^2] PauliMatrix[2])

Show first order Dyson term to QuantumOperator (using externally the Wolfram Quantum Framework):

In[23]:=
dyson = PacletSymbol[ "Wolfram/QuantumFramework", "Wolfram`QuantumFramework`QuantumOperator"][ 1 + PacletSymbol[ "Wolfram/QuantumFramework", "Wolfram`QuantumFramework`QuantumOperator"][ ResourceFunction["DysonTerms"][Hchirped, 1, Dot, -3]], "Parameters" -> {\[CapitalOmega]0, \[Tau], \[Kappa], \[FormalCapitalT]}];
In[24]:=
dyson // TraditionalForm
Out[24]=

Find the Hamiltonian in terms of QuantumOperator:

In[25]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/01263cf7-4fc9-4d56-abfb-046a8f7d6b31"]

Show the first order approximation is good when this value is << 1:

In[26]:=
dysonCondition[\[CapitalOmega]0_, \[Tau]_, \[Kappa]_] := (\[CapitalOmega]0 \[Tau] Sqrt[\[Pi]])/( 2 (1 + \[Kappa]^2 \[Tau]^4)^(1/4))

Case Ω0=1, τ = 1, τ = 10

Use PacletSymbol QuantumEvolve and QuantumState for computing the evolution:

In[27]:=
U = PacletSymbol[ "Wolfram/QuantumFramework", "Wolfram`QuantumFramework`QuantumEvolve"][HchirpedOp[1., 1., 10.], None, {t, -3, 3}]; \[Psi] = U[ PacletSymbol[ "Wolfram/QuantumFramework", "Wolfram`QuantumFramework`QuantumState"]["+"]];

Moderate agreement:

In[28]:=
dysonCondition[1., 1., 10.]
Out[28]=

Plot the result from numerically solving the evolution:

In[29]:=
Plot[Evaluate@\[Psi][t]["ProbabilityList"], {t, -3, 3}, PlotRange -> All, AxesLabel -> {"t", "Probability"}, LabelStyle -> 13]
Out[29]=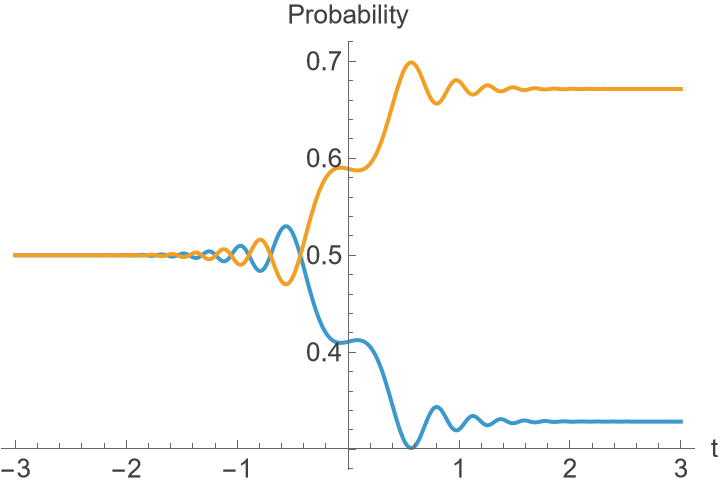

Plot result from the Dyson operator:

In[30]:=
Plot[Evaluate[ dyson[1., 1., 10., t][ PacletSymbol[ "Wolfram/QuantumFramework", "Wolfram`QuantumFramework`QuantumState"]["+"]]["Normalize"][ "ProbabilityList"]], {t, -3, 3}, AxesLabel -> {"t", "Probability"}, LabelStyle -> 13]
Out[30]=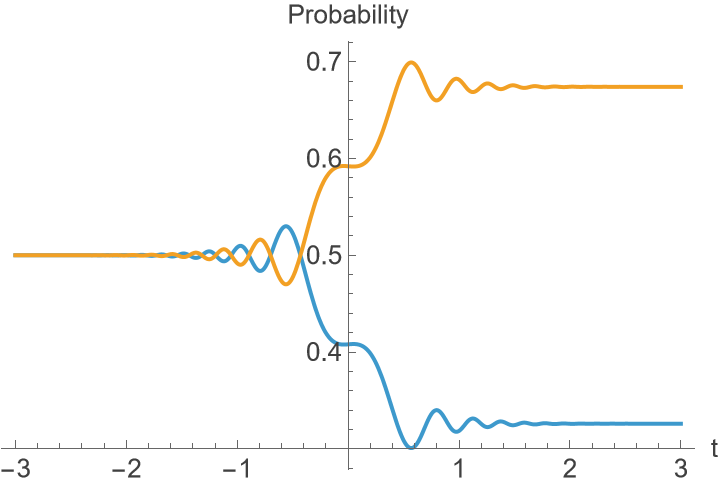

Case Ω0=25, τ = 30, τ = 15

Same procedure as the previous case (now we evolve the state |0〉):

In[31]:=
U = PacletSymbol[ "Wolfram/QuantumFramework", "Wolfram`QuantumFramework`QuantumEvolve"][ HchirpedOp[25., 30., 15.], None, {t, -3, 3}]; \[Psi] = U[ PacletSymbol[ "Wolfram/QuantumFramework", "Wolfram`QuantumFramework`QuantumState"]["0"]];

There will not be good agreement for this case:

In[32]:=
dysonCondition[25, 30, 15.]
Out[32]=

Plot the result from numerically solving the evolution:

In[33]:=
Plot[Evaluate@\[Psi][t]["ProbabilityList"], {t, -3, 3}, PlotRange -> All, AxesLabel -> {"t", "Probability"}, LabelStyle -> 13]
Out[33]=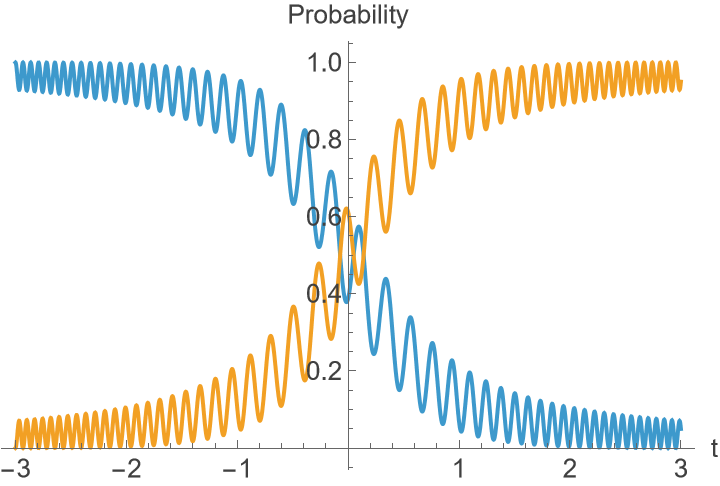

Plot result from Dyson:

In[34]:=
Plot[Evaluate[ dyson[25., 30, 15., t][ PacletSymbol[ "Wolfram/QuantumFramework", "Wolfram`QuantumFramework`QuantumState"]["0"]]["Normalize"][ "ProbabilityList"]], {t, -3, 3}, PlotRange -> {0, 1}, AxesLabel -> {"t", "Probability"}, LabelStyle -> 13]
Out[34]=

Properties and Relations (9) 

Relation to Magnus expansion (9) 

Load the function for computing terms of Magnus expansion:

In[35]:=
MagnusTerms = ResourceFunction["MagnusTerms"]
Out[35]=

For the first order term D1=Ω1 they have the same form:

In[36]:=
MagnusTerms[\[FormalCapitalB], 1, "TimeIntegration" -> True] == ResourceFunction["DysonTerms"][\[FormalCapitalB], 1]/(-I)
Out[36]=

Second order Dyson term expressed in terms of Magnus terms :

In[37]:=
MagnusTerms[\[FormalCapitalB], 2, "TimeIntegration" -> True] + 1/2 MagnusTerms[\[FormalCapitalB], 1, "TimeIntegration" -> True] ** MagnusTerms[\[FormalCapitalB], 1, "TimeIntegration" -> True]
Out[37]=

For the second order Dyson term, it is not trivial to see they are equal:

In[38]:=
ResourceFunction["DysonTerms"][\[FormalCapitalB], 2]/(-I)^2
Out[38]=

Define a time dependent operator in the Pauli basis:

In[39]:=
ClearAll[h1, \[CapitalDelta], \[Omega], A, \[Sigma]] h1[t_] := \[CapitalDelta]/2 PauliMatrix[3] + A Cos[\[Omega] t] PauliMatrix[1] + A Sin[\[Omega] t] PauliMatrix[2]

Result from Dyson:

In[40]:=
res1 = ResourceFunction["DysonTerms"][h1, 2, Dot]/(-I)^2;

Result from Magnus:

In[41]:=
res2 = MagnusTerms[h1, 2, Dot, "TimeIntegration" -> True] + 1/2 MagnusTerms[h1, 1, Dot, "TimeIntegration" -> True] . MagnusTerms[h1, 1, Dot, "TimeIntegration" -> True];
In[42]:=
FullSimplify[res1 - res2]
Out[42]=

Dyson third order term:

In[43]:=
res1 = ResourceFunction["DysonTerms"][h1, 3, Dot]/(-I)^3;

In[44]:=
res2 = With[{\[CapitalOmega]1 = MagnusTerms[h1, 1, Dot, "TimeIntegration" -> True], \[CapitalOmega]2 = MagnusTerms[h1, 2, Dot, "TimeIntegration" -> True], \[CapitalOmega]3 = MagnusTerms[h1, 3, Dot, "TimeIntegration" -> True]}, \[CapitalOmega]3 + 1/2 (\[CapitalOmega]1 . \[CapitalOmega]2 + \[CapitalOmega]2 . \[CapitalOmega]1) + 1/6 \[CapitalOmega]1 . \[CapitalOmega]1 . \[CapitalOmega]1];
In[45]:=
res1 - res2 // Simplify
Out[45]=

For the fourth term we have + . In general, a Dyson term is generated by the non-commutative products of Magnus terms of the corresponding order, with a 1/n! factor introduced by the number of terms in that product.

Possible Issues (2) 

If supplying an algebraic operation, it has to be one compatible with NonCommutativeAlgebra:

In[46]:=
ResourceFunction["DysonTerms"][3, \[FormalCapitalB], KroneckerProduct]
Out[46]=

However it is possible to enforce a desired operation by defining a custom algebra:

In[47]:=
alg = NonCommutativeAlgebra[<|"Multiplication" -> KroneckerProduct|>]; ResourceFunction["DysonTerms"][\[FormalCapitalB], 3, alg]
Out[48]=

Publisher

Bruno Tenorio

Version History

  • 1.0.0 – 17 November 2025

Related Resources

License Information