Basic Examples (11)
Start with a 2×3 polynomial matrix in two variables, one of which will be used as an algebraic extension:
The polynomial defining the extension:
Reduce to row echelon form over the finite extension field of integers mod 7 with 73=343 elements, given as 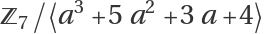 :
:
Compute the inverse of the submatrix comprised of the first two columns:
Check that this inverse multiplied by mat gives the 2×2 identity matrix:
Use the last column as a right-hand side for a matrix equation:
Check the result:
Find a basis for the null space of the full matrix:
Check that it has only null vectors for mat:
Since there are three columns and the null space is generated by one vector, the rank must be 2:
Compute the characteristic polynomial for the matrix augmented by a row of ones:
Scope (2)
One need not use an extension field:
Verify the inverse:
Apart from cancellation of factors, the denominators in the inverse will be constant multiples of the matrix determinant:
Use an operator form of LinearAlgebraMod:
Check the solution:
Use an operator form of LinearAlgebraMod with operation and modulus both specified:
Use a matrix for the right-hand side:
Check that first column agrees with the previous solution:
Check that the result is correct:
Properties and Relations (2)
Define a matrix of integers:
For integer matrices, operations supported by LinearAlgebraMod are equivalent to their built-in counterparts using the Modulus option:
Possible Issues (2)
Symbolic linear algebra can suffer from expression swell (the phenomenon wherein outputs and/or intermediate computations get much larger than inputs).
Define a random polynomial matrix generator:
Create a random 3×3 matrix of polynomials in two variables with up to seven terms having coefficients between 0 and 70, each of which can have a degree up to 4:
Solve the system:
Check the result:
Note the difference in size between input and result:
Create a 6×6 example:
This takes significantly longer:
The factor between output and input sizes has also grown:
Also note that using the built-in LinearSolve for the non-modular case is also on the slow side, though faster than LinearAlgebraMod:
It produces a similarly large result:
The determinant can be found somewhat faster:
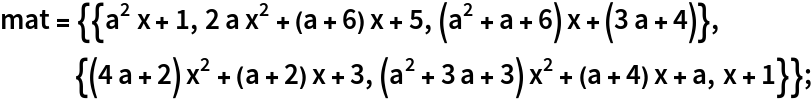
![]() :
: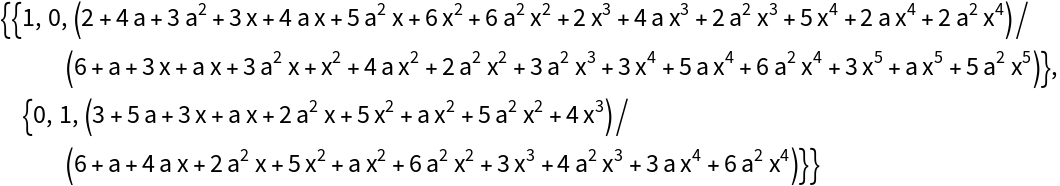
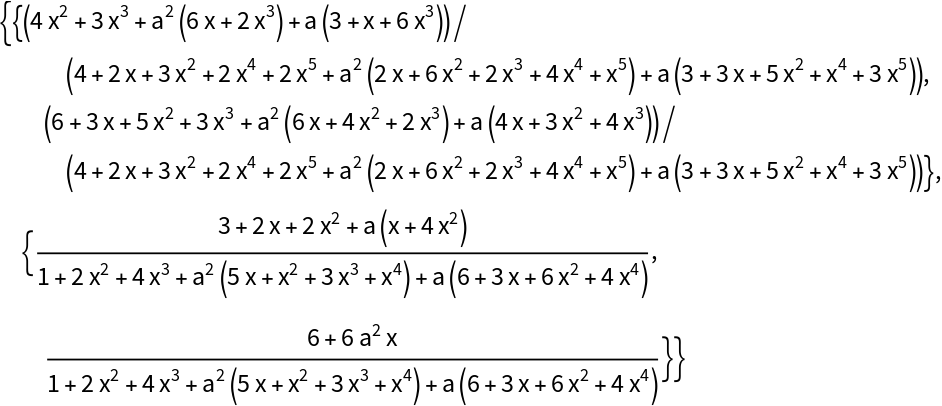
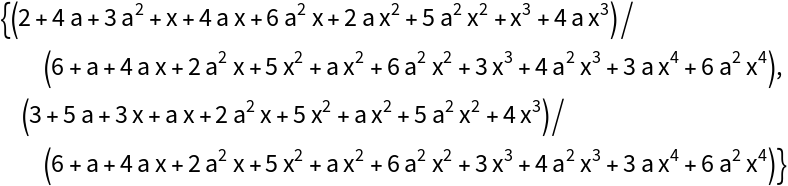
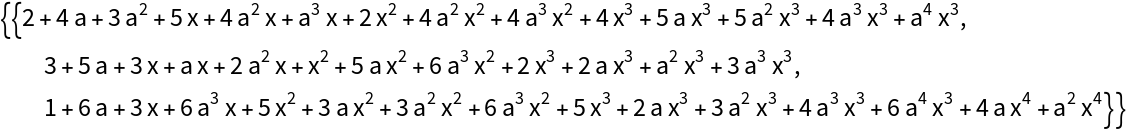
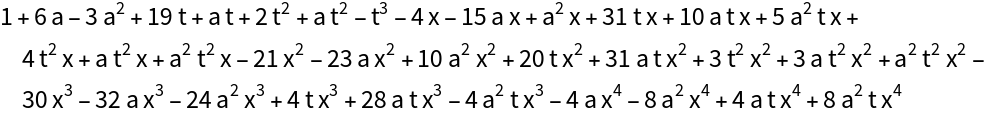
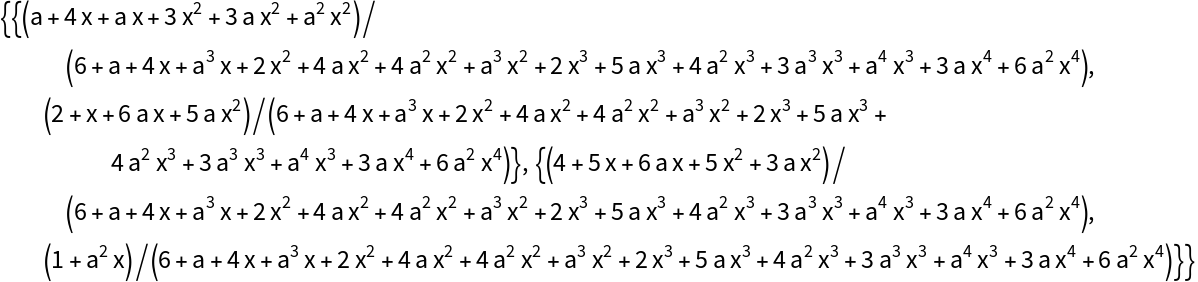
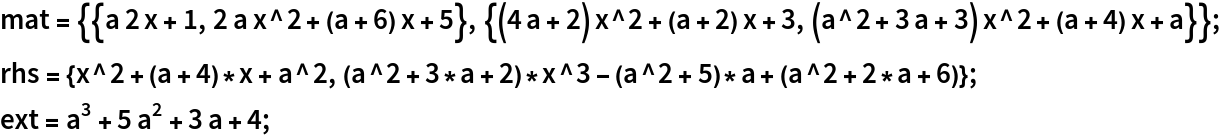
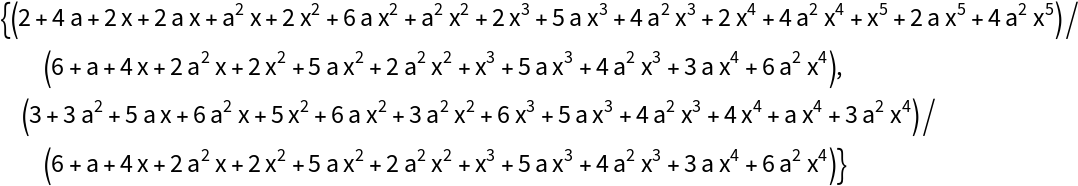
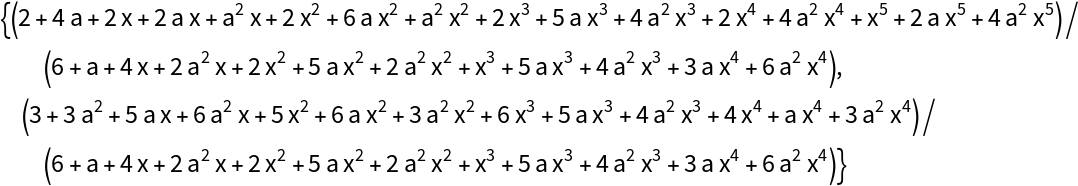
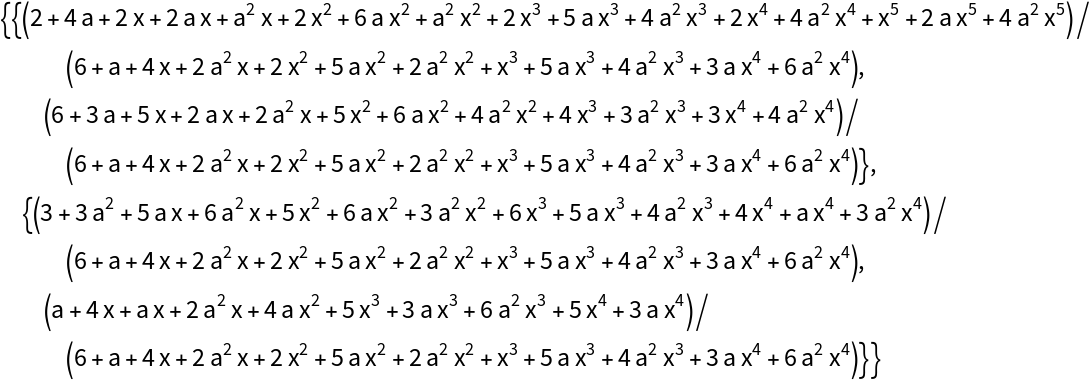
![randomPolynomialMatrix[{r_, c_}, deg_, height_, vars_List, nterms_] :=
Table[randomPolynomial[deg, height, vars, nterms], {r}, {c}]
randomPolynomial[deg_, height_, vars_, nterms_] := RandomInteger[{0, height - 1}, nterms] . Table[randomMonomial[deg, vars], nterms]
randomMonomial[deg_, vars_] := Apply[Times, vars^RandomInteger[{0, deg}, Length[vars]]]](https://www.wolframcloud.com/obj/resourcesystem/images/d80/d802e1b4-90c7-4f54-99d7-ce6aea20792e/1079ed4f72c9e1bf.png)
![SeedRandom[1234];
dim = 3;
deg = 4;
mod = 71;
randpolymat = randomPolynomialMatrix[{dim, dim}, deg, mod, {x, y}, 7];
rhs = Table[randomPolynomial[deg, mod, {x, y}, 7], dim];](https://www.wolframcloud.com/obj/resourcesystem/images/d80/d802e1b4-90c7-4f54-99d7-ce6aea20792e/5270df314bf858c1.png)
![SeedRandom[1234];
dim = 6;
deg = 4;
mod = 7;
rpm = randomPolynomialMatrix[{dim, dim}, deg, mod, {x, y}, 7];
rhs = Table[randomPolynomial[deg, mod, {x, y}, 7], dim];](https://www.wolframcloud.com/obj/resourcesystem/images/d80/d802e1b4-90c7-4f54-99d7-ce6aea20792e/6fd2ea7bb7e96fc9.png)