Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Measure the bandwidth-modified two-sample phase/frequency stability
ResourceFunction["ModifiedAllanDeviation"][data,r,taus] calculates the bandwidth-modified two-sample deviation of data along sample times taus at rate r. |
| {{n}} | attempts to place n logarithmically-spaced samples |
| d | places logarithmic spaced samplings with log base d |
| {τ1,τ2,…} | tries to use the specified sample times |
| All | uses all possible sample times |
| Automatic | tries to place a reasonable amount of samples along the whole possible time range |
Calculate the overlapping modified Allan deviation of white noise at a rate of 0.1 for automatically chosen sampling points:
| In[1]:= |
| Out[2]= | 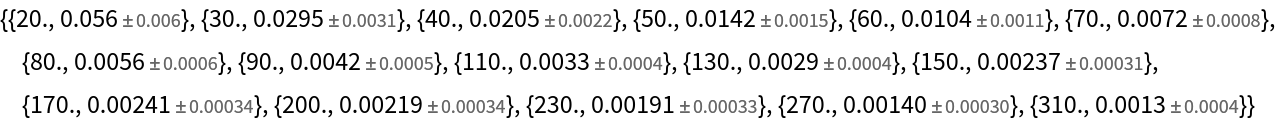 |
Plot the results:
| In[3]:= |
| Out[3]= | 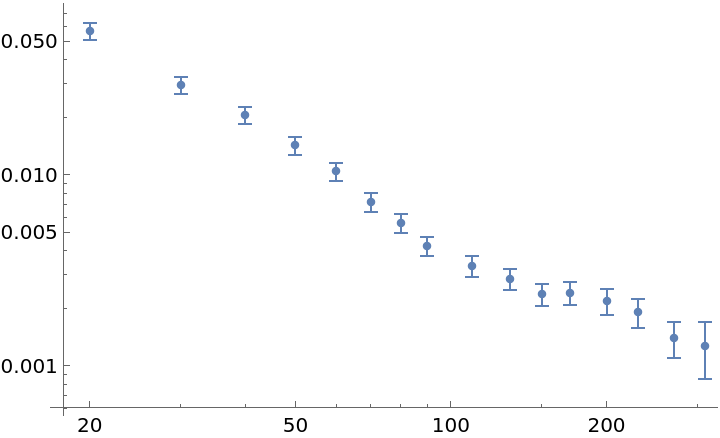 |
Display the overlapping modified Allan deviation of white noise at a rate of 0.1 for certain sampling points:
| In[4]:= | ![data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"];
adev = ResourceFunction["ModifiedAllanDeviation"][data, 0.1, {20, 50, 100, 200}];
ListLogLogPlot[adev, GridLines -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/73d232caeb4dca1f.png) |
| Out[6]= | 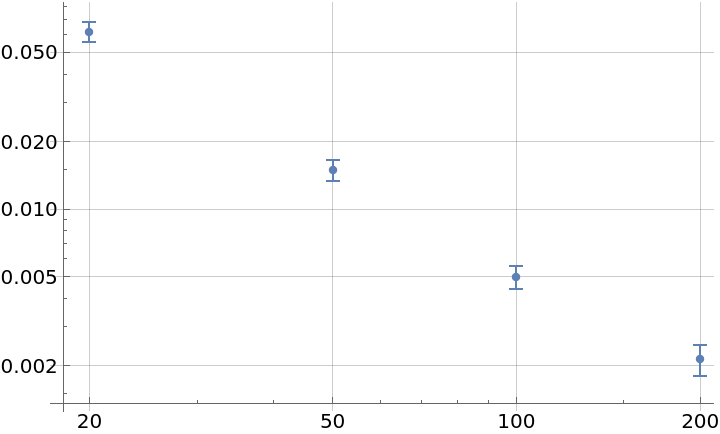 |
Sample at all possible times:
| In[7]:= | ![data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"];
adev = ResourceFunction["ModifiedAllanDeviation"][data, 1, All];
ListLogLogPlot[adev]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/116144ff6da70a9b.png) |
| Out[9]= | 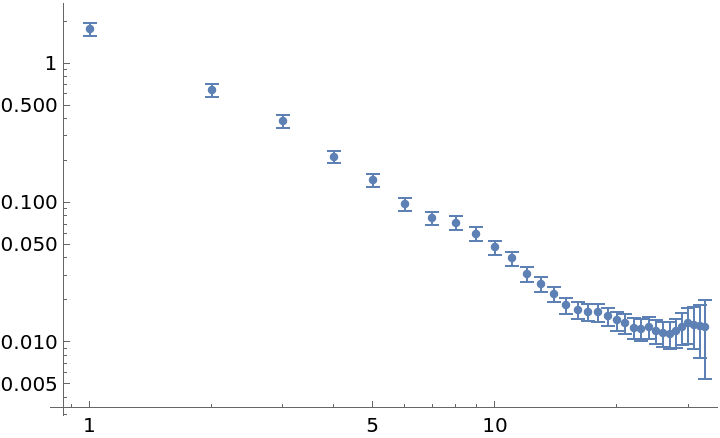 |
Try to sample at five different time values:
| In[10]:= | ![data = RandomFunction[WhiteNoiseProcess[1], {500}]["Values"];
adev = ResourceFunction["ModifiedAllanDeviation"][data, 1, {{5}}];
ListLogLogPlot[adev]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/39c3bd7e24871537.png) |
| Out[12]= | 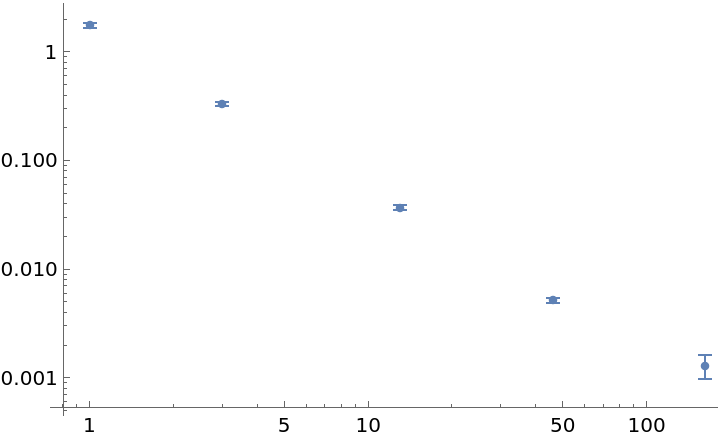 |
The function will try to use a fast evaluation method when the data array is fully real, and otherwise prints a warning:
| In[13]:= | ![data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"];
adev = ResourceFunction["ModifiedAllanDeviation"][data~Join~{Pi}, 1, Automatic];
ListLogLogPlot[adev]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/029a342ce3b6de93.png) |
| Out[15]= | 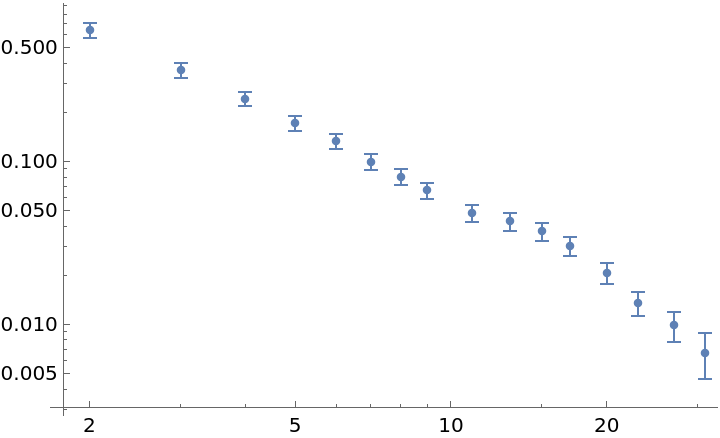 |
"FrequencyData" accepts a Boolean as argument. True signals the use of frequency data as opposed to phase data:
| In[16]:= | ![data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"];
adev = ResourceFunction["ModifiedAllanDeviation"][data, 1, All, "FrequencyData" -> True];
ListLogLogPlot[adev]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/37ec81efa16039b1.png) |
| Out[18]= | 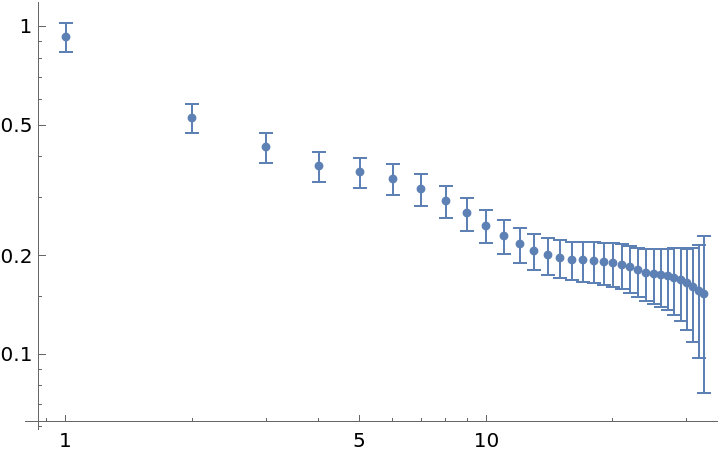 |
"Overlapping" accepts a Boolean as argument. False signals the use of non-overlapping strides in the deviation sampling:
| In[19]:= | ![data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"];
adev = ResourceFunction["ModifiedAllanDeviation"][data, 1, All, "Overlapping" -> False];
ListLogLogPlot[adev]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/2d80ff7cec6ba688.png) |
| Out[21]= | 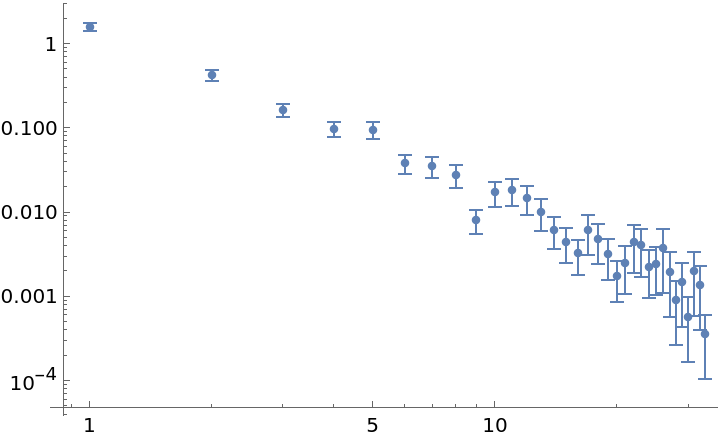 |
Distinguish a random walk from white noise by their distinct slopes:
| In[22]:= | ![datas = N[
RandomFunction[#, {10000}]["Values"]] & /@ {WhiteNoiseProcess[], RandomWalkProcess[0.5]};
adevs = ResourceFunction["ModifiedAllanDeviation"][#, 1, Automatic] & /@ datas;
ListLogLogPlot[adevs]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/728eaefa18120d9b.png) |
| Out[24]= | 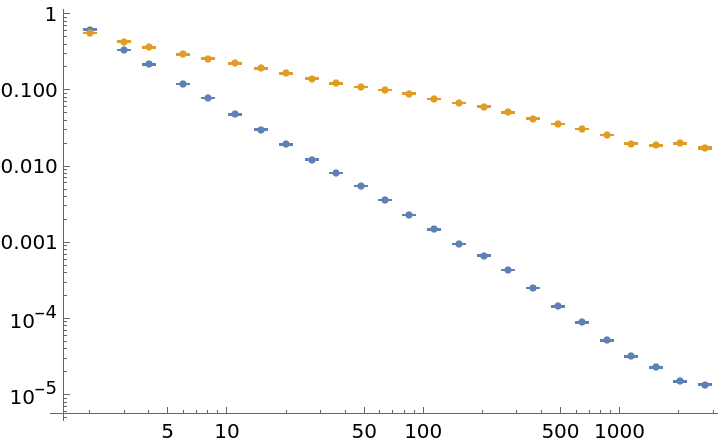 |
Detect a drift in frequency data by a rising slope in longer sample times:
| In[25]:= | ![data = RandomFunction[WhiteNoiseProcess[], {10000}]["Values"] + Accumulate[ConstantArray[10^-4, 10001]];
adev = ResourceFunction["ModifiedAllanDeviation"][data, 1.0, Automatic, "FrequencyData" -> True];
ListLogLogPlot[adev]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/556f4813d2df28ba.png) |
| Out[27]= | 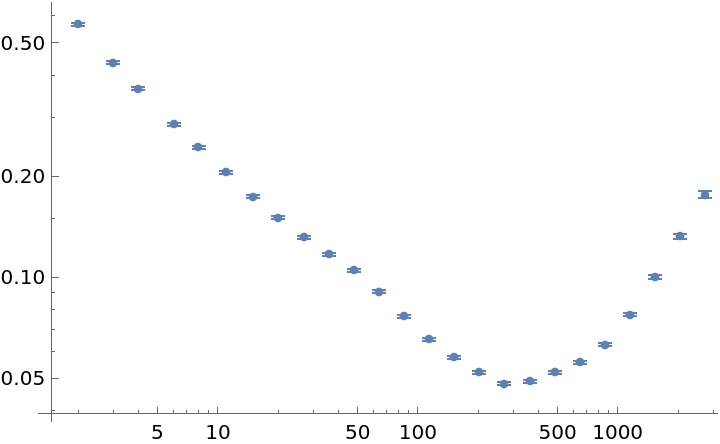 |
Using the fast algorithm is approximately two times faster:
| In[28]:= |
| Out[29]= |
| In[30]:= |
| Out[30]= |
The function can process Around objects as well as exact inputs directly:
| In[31]:= | ![data = Table[
Around[RandomVariate[NormalDistribution[0, 2]], 2], {i, 1, 1000}];
adev = ResourceFunction["ModifiedAllanDeviation"][data, 1, Automatic];
ListLogLogPlot[adev]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/66fb8fb6258cecf5.png) |
| Out[33]= | 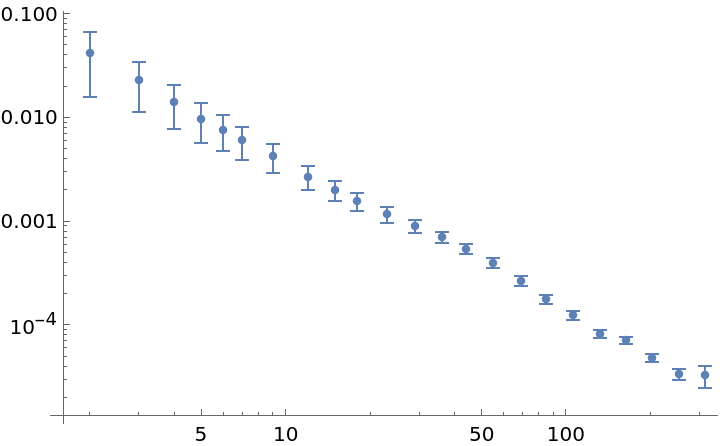 |
Compare ModifiedAllanDeviation with the AllanDeviation resource function:
| In[34]:= |
| In[35]:= | ![ListLogLogPlot[{ResourceFunction["ModifiedAllanDeviation"][data, .1, Automatic], ResourceFunction["AllanDeviation"][data, 0.1, Automatic]}]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/2717ee3734536e0e.png) |
| Out[35]= | 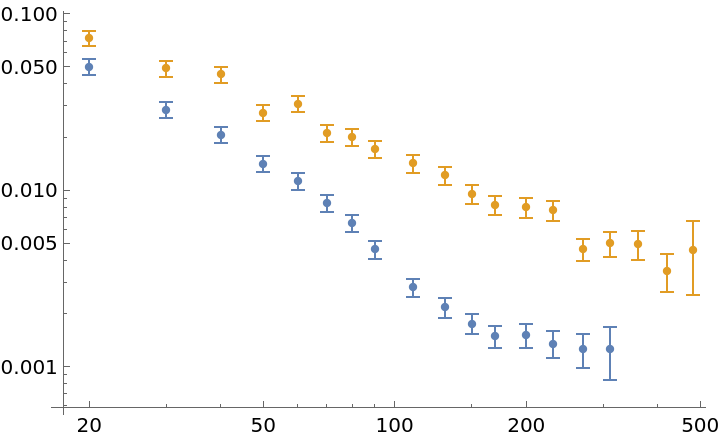 |
Requesting a certain amount of samples will not necessarily result in this amount of deviations:
| In[36]:= |
| Out[37]= |
The function can distinguish between white phase noise and flicker noise (pink noise), as opposed to the plain Allan deviation:
| In[38]:= | ![pink = Rescale[First@AudioData[AudioGenerator["Pink", 1.0]]];
white = Rescale[
RandomFunction[WhiteNoiseProcess[1], {Length[pink] - 1}]["Values"]];
pinkmadev = ResourceFunction["ModifiedAllanDeviation"][pink, 1, Automatic];
whitemadev = ResourceFunction["ModifiedAllanDeviation"][white, 1, Automatic];
pinkadev = ResourceFunction["AllanDeviation"][pink, 1, Automatic];
whiteadev = ResourceFunction["AllanDeviation"][white, 1, Automatic];
ListLogLogPlot[{pinkmadev, whitemadev, pinkadev, whiteadev}, PlotLegends -> {"Modified Allan dev. pink", "Modified Allan dev. white", "Allan dev. pink", "Allan dev. white"}]](https://www.wolframcloud.com/obj/resourcesystem/images/cf6/cf6be746-cae4-4089-8467-da3a17562896/6a53d04bea9055dc.png) |
| Out[44]= | 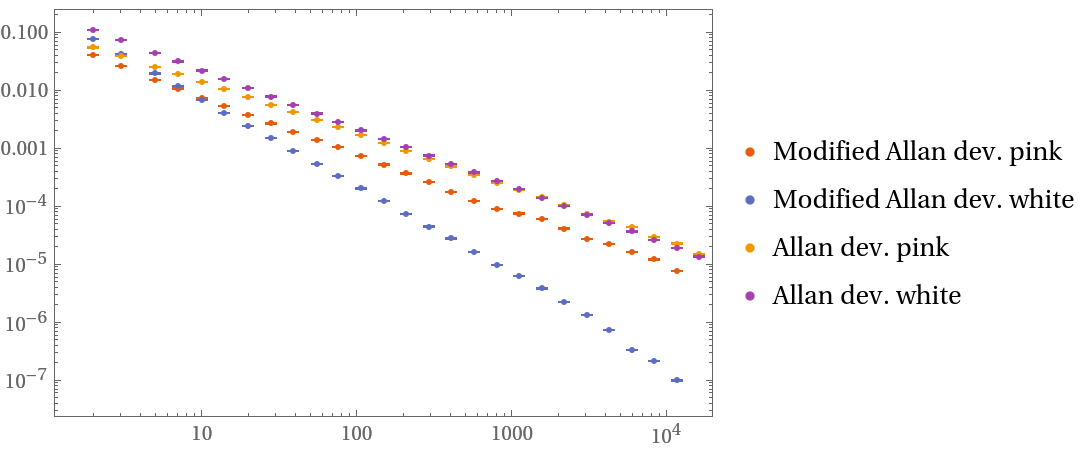 |
This work is licensed under a Creative Commons Attribution 4.0 International License