Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AllanDeviation

Source Notebook

Measure the two-sample phase/frequency stability

Contributed by: Julien Kluge

ResourceFunction["AllanDeviation"][data,r,taus]

calculates the two-sample deviation of data along sample times taus at rate r.

Details and Options

The Allan deviation is the square root of the two-sample variance, which is used to characterize the frequency/phase stability of an oscillator.
The output usually comes in the format {τ,Around[σ,δσ]} where δσ denotes the statistical uncertainty related to the deviation σ.
The argument taus can be specified as:
{{n}}attempts to place n logarithmic spaced samples
dplaces logarithmic spaced samplings with log base d
{τ1,τ2,…}tries to use the specified sample times
Alluses all possible sample times
Automatictries to place a reasonable amount of samples along the whole possible time range
For a list of reals as a data argument, ResourceFunction["AllanDeviation"] will use a fast, compiled algorithm. Otherwise, valid inputs are exact expressions and/or Around.
The rate r must be a positive, numeric quantity.
Supported options are:
"Overlapping"Truewhether the Allan deviation is overlapping
"FrequencyData"Falsewhether data is a list of frequencies, or False for phase data

Examples

Basic Examples (2) 

Calculate the overlapping Allan deviation of white noise at a rate of 0.1 for automatically chosen sampling points:

In[1]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; adev = ResourceFunction["AllanDeviation"][data, 0.1, Automatic]
Out[2]=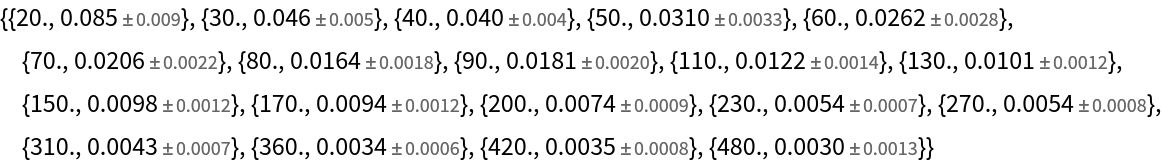

Plot the results:

In[3]:=
ListLogLogPlot[adev]
Out[3]=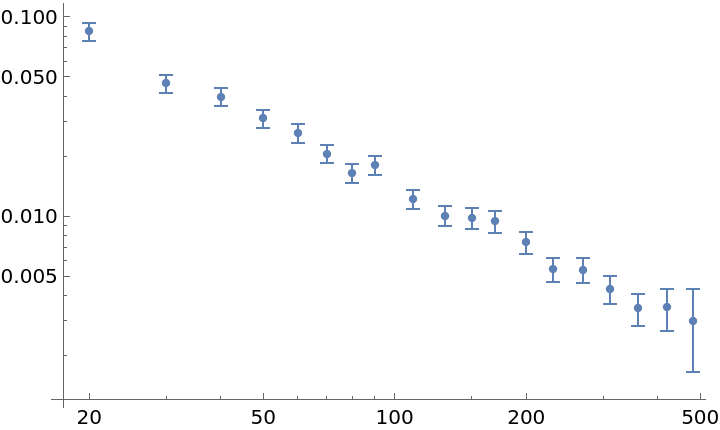

Display the overlapping Allan deviation of white noise at a rate of 0.1 for specified sampling points:

In[4]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; adev = ResourceFunction["AllanDeviation"][data, 0.1, {20, 50, 100, 200, 400}]; ListLogLogPlot[adev, GridLines -> Automatic]
Out[6]=

Scope (2) 

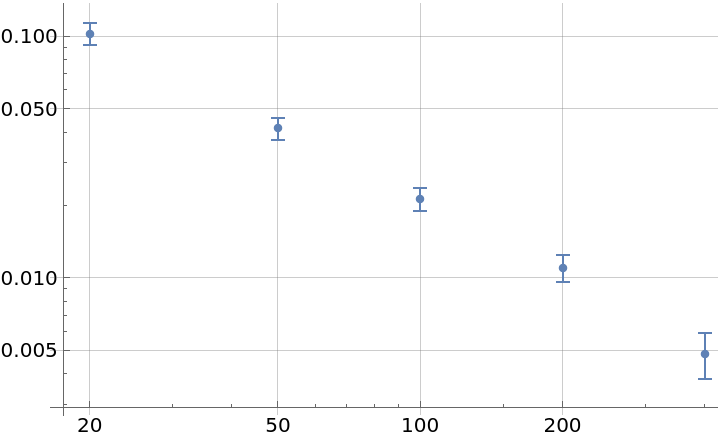Sample at all possible times:

In[7]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; adev = ResourceFunction["AllanDeviation"][data, 1, All]; ListLogLogPlot[adev]
Out[9]=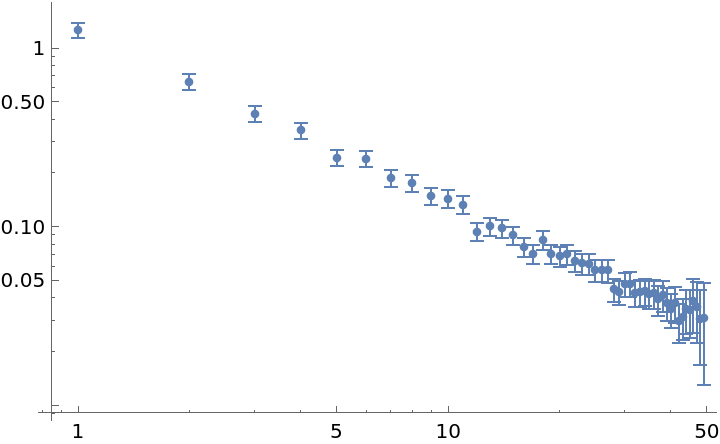

Try to sample at five different time values:

In[10]:=
adev = ResourceFunction["AllanDeviation"][data, 1, {{5}}]; ListLogLogPlot[adev]
Out[11]=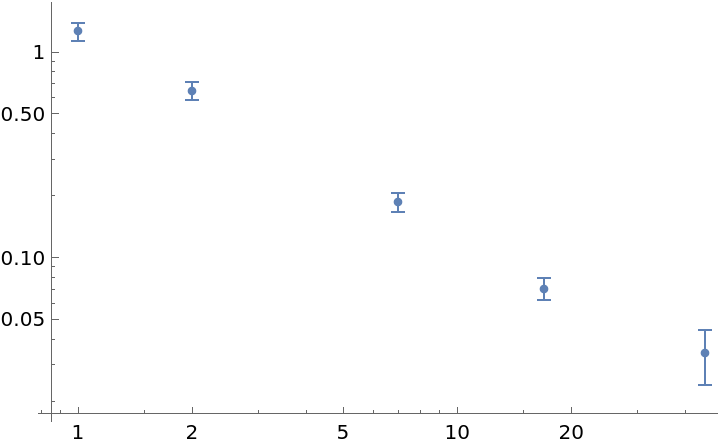

The function will try to use a fast evaluation method when the data array is fully real, and otherwise prints a warning:

In[12]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; adev = ResourceFunction["AllanDeviation"][data~Join~{Pi}, 1, Automatic]; ListLogLogPlot[adev]
Out[14]=

Options (2) 

FrequencyData (1) 

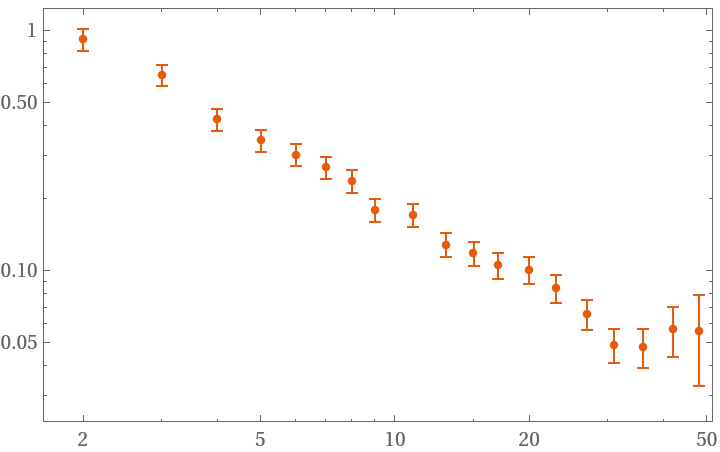"FrequencyData" accepts a Boolean value. True signals the use of frequency data as opposed to phase data:

In[15]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; adev = ResourceFunction["AllanDeviation"][data, 1, All, "FrequencyData" -> True]; ListLogLogPlot[adev]
Out[16]=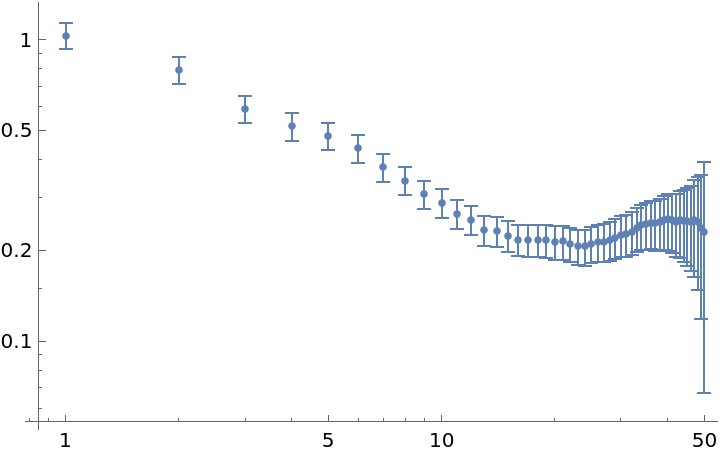

Overlapping (1) 

"Overlapping" accepts a Boolean value. False signals the use of non-overlapping strides in the deviation sampling:

In[17]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; adev = ResourceFunction["AllanDeviation"][data, 1, All, "Overlapping" -> False]; ListLogLogPlot[adev]
Out[18]=

Applications (2) 

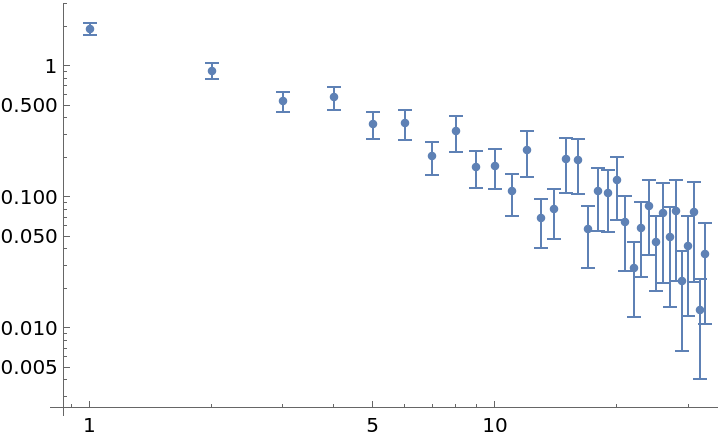Distinguish a random walk from white noise by their distinct slopes:

In[19]:=
datas = N[ RandomFunction[#, {10000}]["Values"]] & /@ {WhiteNoiseProcess[], RandomWalkProcess[0.5]}; adevs = ResourceFunction["AllanDeviation"][#, 1, Automatic] & /@ datas; ListLogLogPlot[adevs]
Out[20]=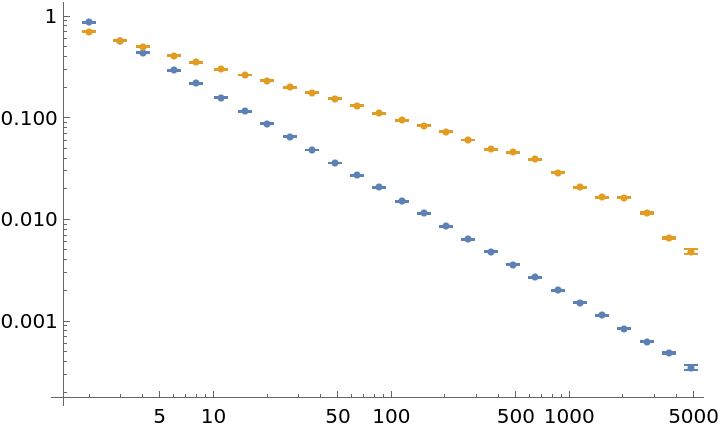

Detect a drift in frequency data by a rising slope in longer sample times:

In[21]:=
data = RandomFunction[WhiteNoiseProcess[], {10000}]["Values"] + Accumulate[ConstantArray[10^-4, 10001]]; adev = ResourceFunction["AllanDeviation"][data, 1.0, Automatic, "FrequencyData" -> True]; ListLogLogPlot[adev]
Out[22]=

Properties and Relations (2) 

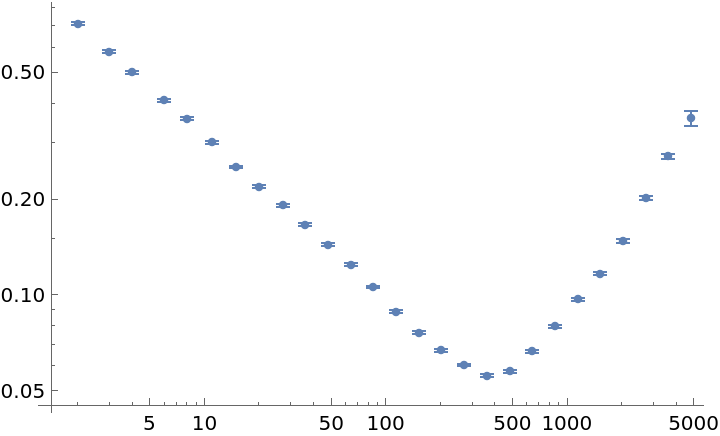Using the fast algorithm for numeric data is approximately two times faster:

In[23]:=
data = RandomFunction[WhiteNoiseProcess[], {1000000}]["Values"]; ResourceFunction["AllanDeviation"][data~Join~{N@Pi}, 1.0, Automatic]; // AbsoluteTiming
Out[24]=
In[25]:=
ResourceFunction["AllanDeviation"][data~Join~{Pi}, 1.0, Automatic]; // AbsoluteTiming
Out[25]=

The function can process Around objects as well as exact inputs directly:

In[26]:=
data = Table[ Around[RandomVariate[NormalDistribution[0, 2]], 2], {i, 1, 1000}]; adev = ResourceFunction["AllanDeviation"][data, 1, Automatic]; ListLogLogPlot[adev]
Out[27]=

Possible Issues (1) 

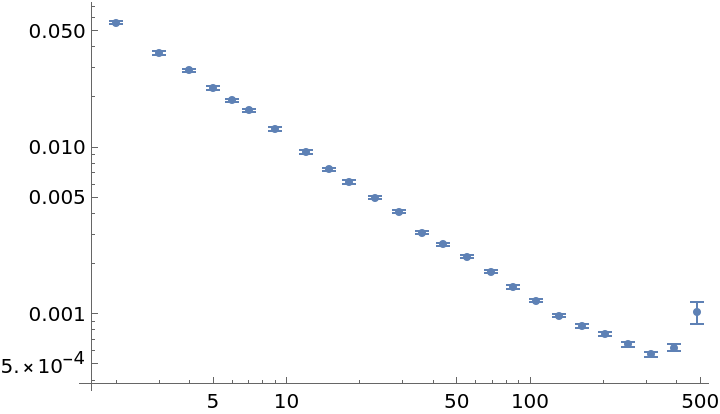Requesting a certain number of samples will not necessarily result in this number of deviations:

In[28]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; ResourceFunction["AllanDeviation"][data, 1.0, {{10}}] // Length
Out[29]=

Publisher

Julien Kluge

Version History

  • 1.0.0 – 11 June 2020

Related Resources

License Information