Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent a hyperbolic line segment or polyline embedded in the Poincaré disk
ResourceFunction["HyperbolicPoincareLine"][{p1,…,pn}] represents the hyperbolic line segments joining a sequence of points pi, embedded in the Poincaré disk. |
A hyperbolic line segment:
| In[1]:= |
|
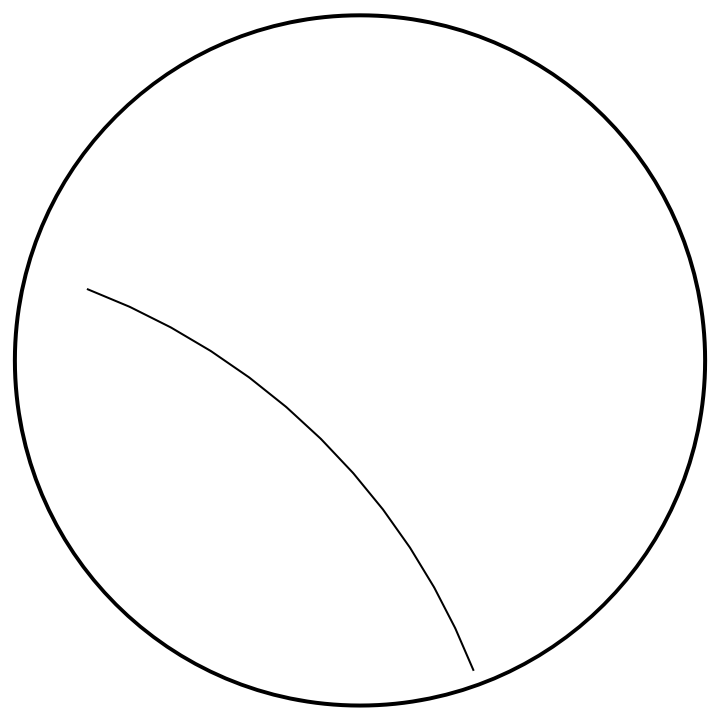
Show the hyperbolic line segment in the Poincaré disk:
| In[2]:= |
|
| Out[2]= |
|
A hyperbolic polyline:
| In[3]:= |
|
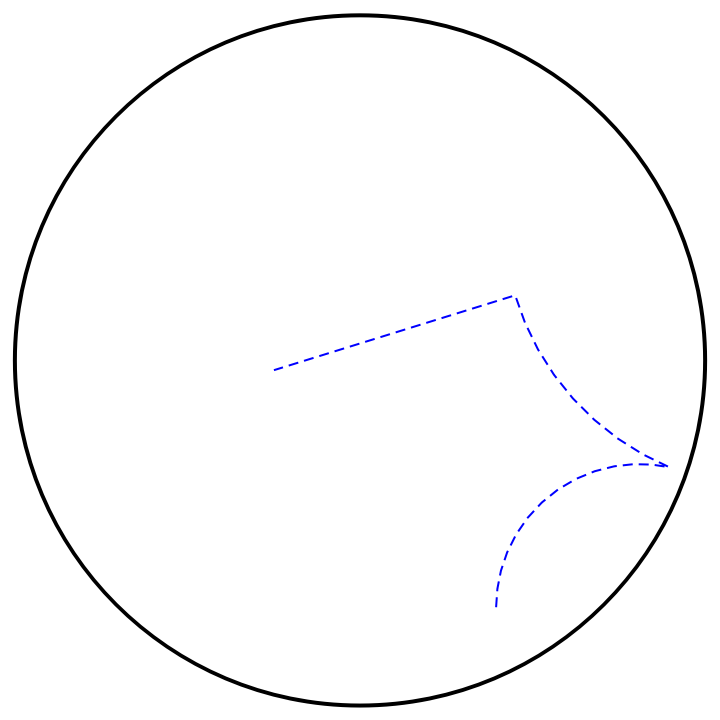
Show the hyperbolic polyline in the Poincaré disk with styling:
| In[4]:= |
|
| Out[4]= |
|
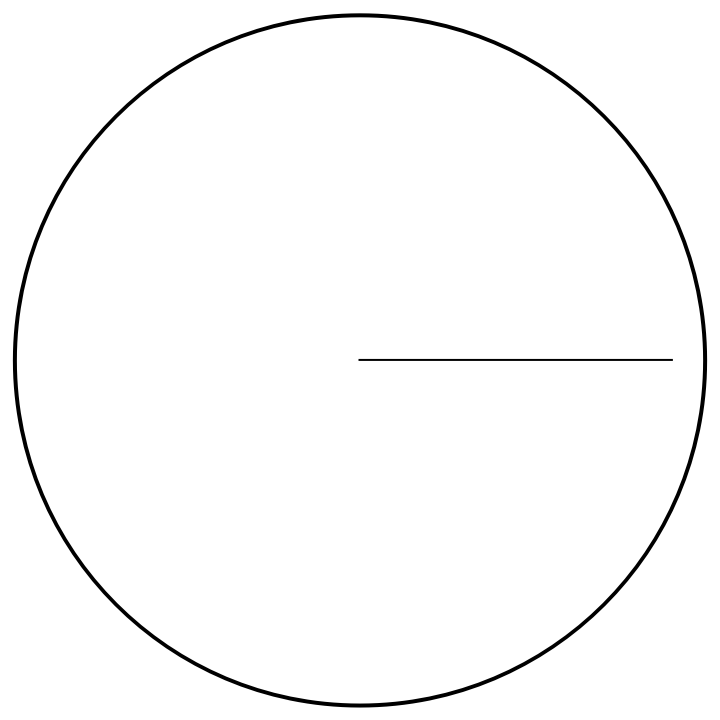
Construct a hyperbolic line segment of given length with one endpoint at the origin:
| In[5]:= |
|
| Out[5]= |
|
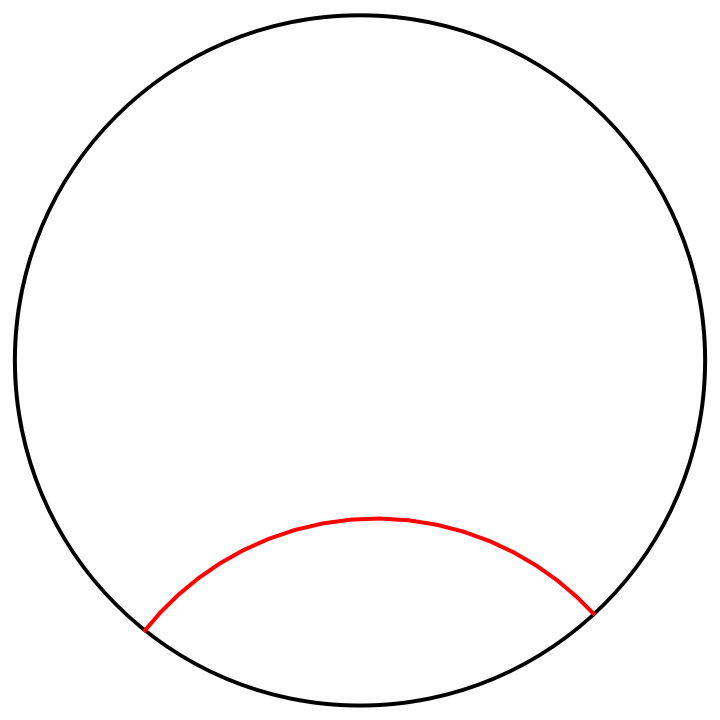
A hyperbolic line segment with endpoints at infinity:
| In[6]:= |
|
| In[7]:= |
|
| Out[7]= |
|
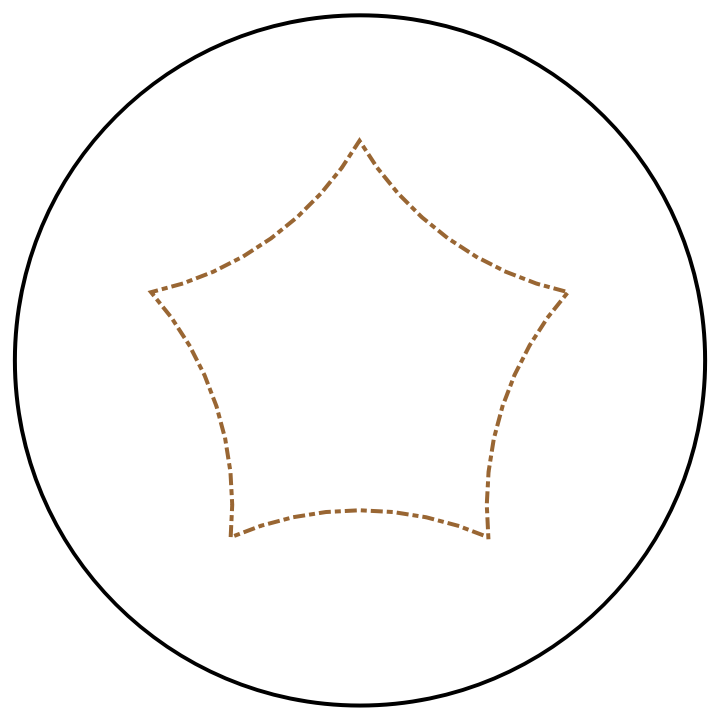
Show the outline of a regular polygon centered at the origin:
| In[8]:= |
![With[{n = 5, r = 3/2}, Graphics[{{Thick, Circle[]}, {Directive[Brown, Thick, DotDashed], ResourceFunction[
"HyperbolicPoincareLine"][{##, #1} & @@ N[CirclePoints[Tanh[r/2], n]]]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/c2f/c2f7a3d2-5c57-4de6-af1b-7fe6da53c80c/6f48e300027a384e.png)
|
| Out[8]= |
|
All vertices of HyperbolicPoincareLine must lie within the unit disk:
| In[10]:= |
|
| Out[10]= |
|
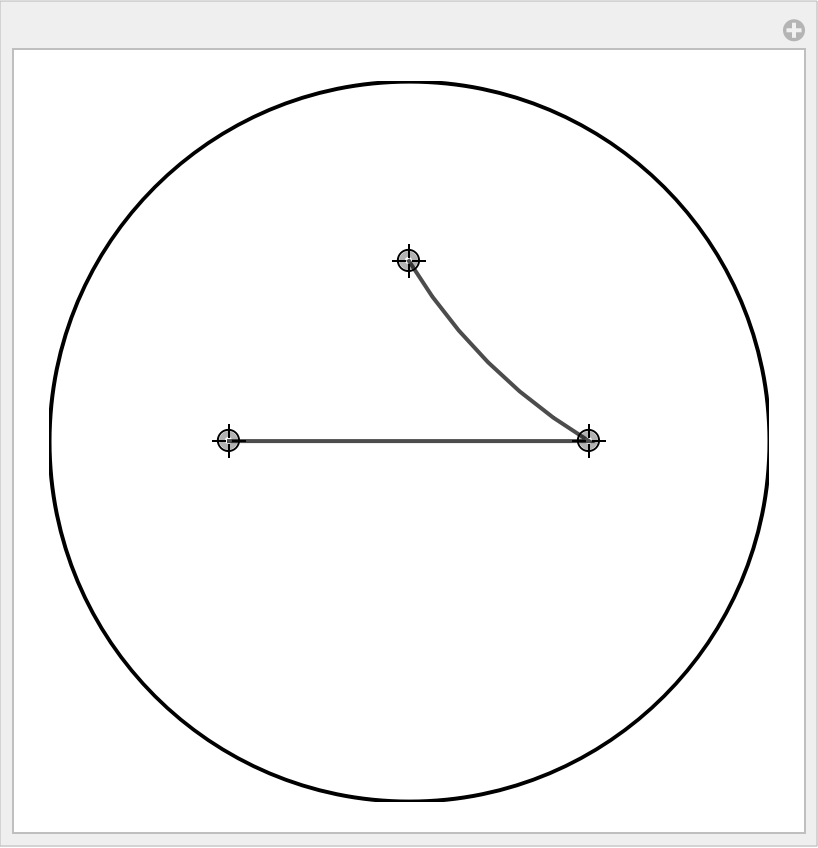
Create a Manipulate of joined points on the Poincaré disk, where points can be added or deleted by Alt-Click:
| In[11]:= |
![Manipulate[pts = Clip[Norm[#], {0, 1}] Normalize[#] & /@ pts; Graphics[{{Thick, Circle[]}, {Directive[Thick, GrayLevel[0.3]], ResourceFunction["HyperbolicPoincareLine"][pts]}}, {
BaseStyle -> {
FilledCurveBoxOptions -> {Method -> {"SplinePoints" -> 18}}}, PlotRange -> 1}], {{pts, {{-0.5, 0.}, {0.5, 0.}, {0., 0.5}}}, Locator, LocatorAutoCreate -> True}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/c2f/c2f7a3d2-5c57-4de6-af1b-7fe6da53c80c/3b0a317ce38a9e81.png)
|
| Out[11]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License