Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the four main points of the Euler line of a triangle
ResourceFunction["EulerLinePoints"][{p1,p2,p3}] returns the circumcenter, centroid, nine-point center and orthocenter of the triangle defined by vertices p1,p2 and p3. |
Find the defining points for the Euler line of three triangle vertices:
| In[1]:= |
| Out[1]= |
Compute points on the Euler line of a 3D triangle:
| In[2]:= |
| Out[2]= |
Show the points and the triangle together:
| In[3]:= | ![Legended[Graphics3D[{{Opacity[0.3, Orange], tri}, {AbsolutePointSize[8], Transpose[{{Red, Cyan, Brown, Green}, Point /@ el}]}}], PointLegend[{Red, Cyan, Brown, Green}, {"circumcenter", "centroid", "nine-point center", "orthocenter"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/bf0/bf0f8354-2580-4008-83c5-3985459a9216/6e18e0424c309d85.png) |
| Out[3]= | 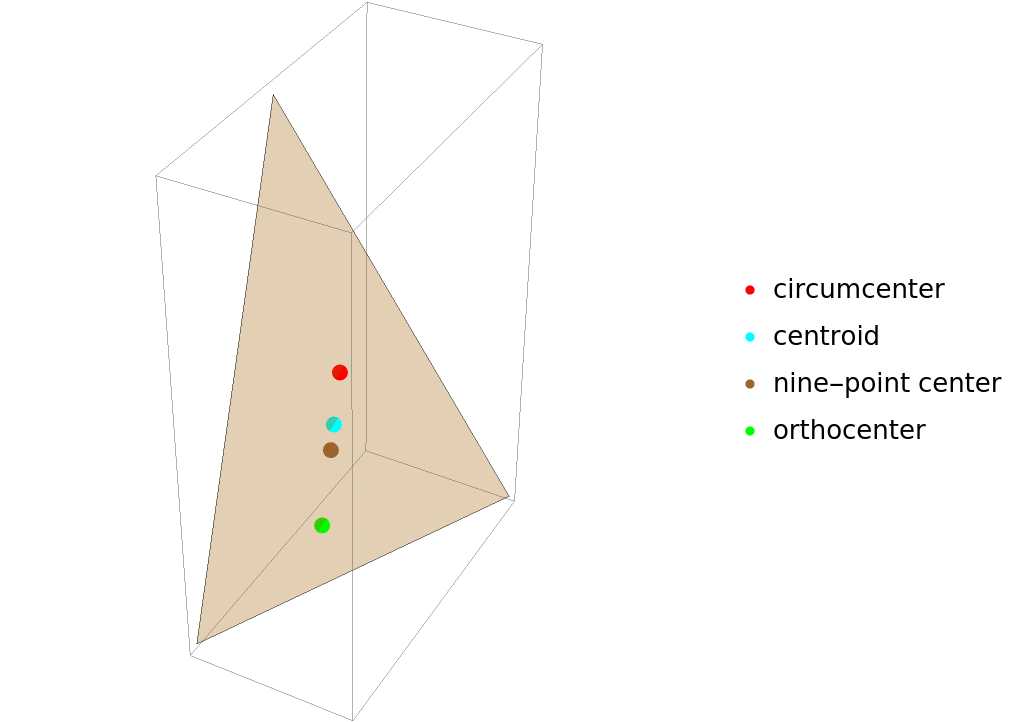 |
A graphic of a triangle with the Euler line (blue), circumcenter|circumcircle|perpendicular bisectors (red), centroid|medians (cyan), nine-point center|circle (brown) and orthocenter|altitudes (green):
| In[4]:= | ![tri = {{-14, -6}, {10, -6}, {4, 12}};
euler = ResourceFunction["EulerLinePoints"][tri];
mids = Mean /@ Subsets[Reverse[tri], {2}];
otherthree = Mean[{#, euler[[4]]}] & /@ tri;
Legended[Graphics[{EdgeForm[Black], White, Thick, Triangle[tri],
Blue, InfiniteLine[Take[euler, 2]], Thin,
Red, InfiniteLine[{euler[[1]], #}] & /@ mids, Circumsphere[tri], Disk[euler[[1]], 0.2],
Cyan, InfiniteLine /@ Transpose[{tri, mids}], Disk[euler[[2]], 0.2],
Brown, Circle[euler[[3]], EuclideanDistance[euler[[3]], mids[[1]]]], Disk[#, .1] & /@ otherthree, Disk[euler[[3]], 0.2],
Green, InfiniteLine[{euler[[4]], #}] & /@ tri, Disk[euler[[4]], 0.2]}], PointLegend[{Red, Cyan, Brown, Green}, {"circumcenter", "centroid", "nine-point center", "orthocenter"}, LegendMarkers -> ConstantArray[Graphics[Disk[]], 3]]]](https://www.wolframcloud.com/obj/resourcesystem/images/bf0/bf0f8354-2580-4008-83c5-3985459a9216/6aef28763b9defc2.png) |
| Out[4]= | 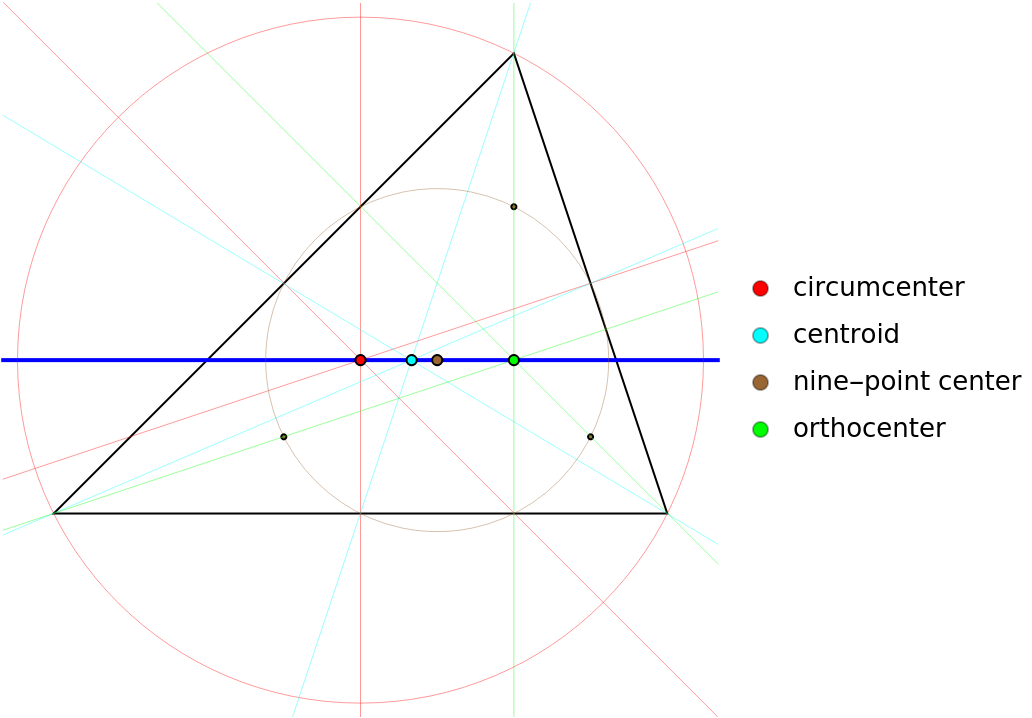 |
This work is licensed under a Creative Commons Attribution 4.0 International License