Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 VectorSubspaceQ

Source Notebook

Determine if the span of one list of vectors is contained in the span of a second list of vectors

Contributed by: Dennis M Schneider

ResourceFunction["VectorSubspaceQ"][list1,list2]

tests whether the span of the first list of vectors is contained in the span of the second list of vectors.

ResourceFunction["VectorSubspaceQ"][list1,list2,var]

performs the same test for lists of functions of var.

Examples

Basic Examples (5) 

The span of the first list is contained in the span of the second list:

In[1]:=
list1 = {{1, 2, 3, 1}, {1, 2, 4, 2}, {2, 4, 7, 3}}; list2 = {{2, 4, 7, 1}, {0, 0, 2, 2}, {1, 2, 0, 2}}; ResourceFunction["VectorSubspaceQ"][list1, list2]
Out[1]=

The span of the second list of vectors is not contained in the span of the first list:

In[2]:=
ResourceFunction["VectorSubspaceQ"][list2, list1]
Out[2]=

Check:

The span of list1 is contained in the span of list2 since every vector in list1 is a linear combination of vectors in list2:

In[3]:=
RowReduce[Join[Transpose[list2], Transpose[list1], 2]] // MatrixForm
Out[9]=

The first and third vectors in list2 are not linear combinations of the vectors in list1:

In[10]:=
RowReduce[Join[Transpose[list1], Transpose[list2], 2]] // MatrixForm
Out[16]=

Scope (5) 

Matrices (3) 

The subspace spanned by the first list of vectors (matrices) is contained in the subspace spanned by the second list:

In[17]:=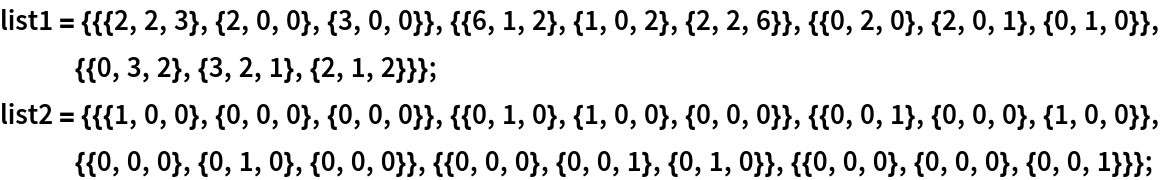
list1 = {{{2, 2, 3}, {2, 0, 0}, {3, 0, 0}}, {{6, 1, 2}, {1, 0, 2}, {2, 2, 6}}, {{0, 2, 0}, {2, 0, 1}, {0, 1, 0}}, {{0, 3, 2}, {3, 2, 1}, {2, 1, 2}}}; list2 = {{{1, 0, 0}, {0, 0, 0}, {0, 0, 0}}, {{0, 1, 0}, {1, 0, 0}, {0, 0, 0}}, {{0, 0, 1}, {0, 0, 0}, {1, 0, 0}}, {{0, 0, 0}, {0, 1, 0}, {0, 0, 0}}, {{0, 0, 0}, {0, 0, 1}, {0, 1, 0}}, {{0, 0, 0}, {0, 0, 0}, {0, 0, 1}}};
In[18]:=
ResourceFunction["VectorSubspaceQ"][list1, list2]
Out[18]=

However, the two subspaces are not equal:

In[19]:=
ResourceFunction["VectorSubspaceQ"][list2, list1]
Out[19]=

Confirm by checking with the resource function SameSpanQ:

In[20]:=
ResourceFunction["SameSpanQ"][list1, list2]
Out[20]=

Function Spaces (2) 

The span of the first list of trigonometric functions is contained in the span of the second list, as can be verified using trigonometric identities:

In[21]:=
ResourceFunction[ "VectorSubspaceQ"][{1, Cos[2 x], Cos[4 x]}, {Cos[x], Cos[x]^2, Cos[x]^4, Sin[x]^4}, x]
Out[21]=

But the two subspaces are not equal:

In[22]:=
ResourceFunction[ "VectorSubspaceQ"][{Cos[x], Cos[x]^2, Cos[x]^4, Sin[x]^4}, {1, Cos[2 x], Cos[4 x]}, x]
Out[22]=

The first function cos(x) is not a linear combination of 1,cos(2x),cos(4x):

In[23]:=
ResourceFunction["VectorSubspaceQ"][{Cos[x]}, {1, Cos[2 x], Cos[4 x]}, x]
Out[23]=

But each of the other functions cos2(x),cos4(x),sin4(x) in the first list is a linear combination of the three functions 1,cos(2x),cos(4x):

In[24]:=
ResourceFunction[ "VectorSubspaceQ"][{Cos[x]^2, Cos[x]^4, Sin[x]^4}, {1, Cos[2 x], Cos[4 x]}, x]
Out[24]=

The even Chebyshev polynomials of the first kind of degree at most 10 form a subspace of the space of all polynomials of degree at most 10:

In[25]:=
Table[ChebyshevT[k, x], {k, 0, 10, 2}]
Out[25]=
In[26]:=
ResourceFunction["VectorSubspaceQ"][ Table[ChebyshevT[k, x], {k, 0, 10, 2}], Table[x^k, {k, 0, 10}], x]
Out[26]=

But the two subspaces are not equal:

In[27]:=
ResourceFunction["VectorSubspaceQ"][Table[x^k, {k, 0, 10}], Table[ChebyshevT[k, x], {k, 0, 10, 2}], x]
Out[27]=

Check with the resource function SameSpanQ:

In[28]:=
Quiet[ResourceFunction["SameSpanQ"][ Table[ChebyshevT[k, x], {k, 0, 10, 2}], Table[x^k, {k, 0, 10}], x]]
Out[28]=

Publisher

Dennis M Schneider

Version History

  • 1.0.0 – 11 October 2019

Related Resources

License Information