Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SameSpanQ

Source Notebook

Determine whether two lists of vectors span the same subspace

Contributed by: Dennis M Schneider

ResourceFunction["SameSpanQ"][list1,list2]

tests whether the span of the first list of vectors is equal to the span of the second list of vectors.

ResourceFunction["SameSpanQ"][list1,list2,var]

performs the same test for lists of functions of var.

Details and Options

The list of vectors may be a list of matrices.

Examples

Basic Examples (1) 

Test whether two lists of vectors in span the same subspace:

In[1]:=
ResourceFunction[ "SameSpanQ"][{{1, 2, 3}, {1, 2, 4}}, {{2, 4, 7}, {2, 4, 9}}]
Out[1]=

Scope (12) 

Vectors in ℂ^n (4) 

Test vectors in :

In[2]:=
list1 = {{2, I, -I, 13 + 5 I}, {1, -I, 1, -1 + 6 I}, {1 - I, 2 + 2 I, -1 + I, 14 - 18 I}, {1 + I, 1 + 2 I, -I, 5 - 3 I}, {1 + I, 1 + I, -1 + I, 5 + I}, {2 + 2 I, 2 - I, 2 - I, -15 + 9 I}}; list2 = {{2, I, -I, 13 + 5 I}, {1, -I, 1, -1 + 6 I}, {1 - I, 2 + 2 I, -1 + I, 14 - 18 I}}; ResourceFunction["SameSpanQ"][list1, list2]
Out[4]=

Since there are six vectors in the first list and only three in the second list, the vectors in the first list must be dependent. Check by computing the rank of the matrix:

In[5]:=
MatrixRank[list1]
Out[5]=

Check that the vectors in the first list are in the span of the vectors in the second list:

In[6]:=
RowReduce[Join[Transpose[list1], Transpose[list2], 2]] // MatrixForm
Out[6]=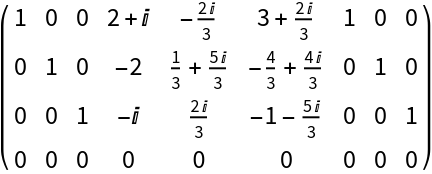

Check that the vectors in the second list are in the span of the vectors in the first list:

In[7]:=
RowReduce[Join[Transpose[list2], Transpose[list1], 2]] // MatrixForm
Out[7]=

Spaces of matrices (4) 

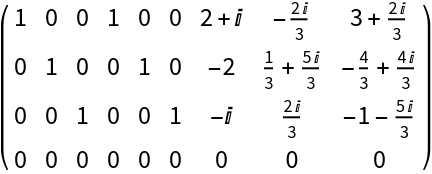The standard basis for the space of 2×4 matrices is:

In[8]:=
basis = Map[Partition[#, 4] &, IdentityMatrix[8]]
Out[8]=

Test whether the following list of eight vectors spans the same subspace as basis:

In[9]:=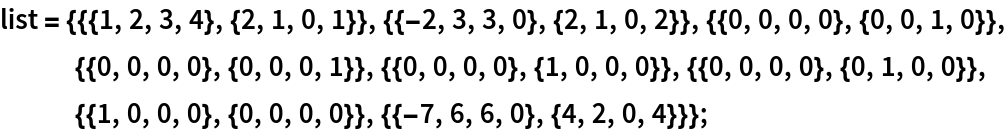
list = {{{1, 2, 3, 4}, {2, 1, 0, 1}}, {{-2, 3, 3, 0}, {2, 1, 0, 2}}, {{0, 0, 0, 0}, {0, 0, 1, 0}}, {{0, 0, 0, 0}, {0, 0, 0, 1}}, {{0, 0, 0, 0}, {1, 0, 0, 0}}, {{0, 0, 0, 0}, {0, 1, 0, 0}}, {{1, 0, 0, 0}, {0, 0, 0, 0}}, {{-7, 6, 6, 0}, {4, 2, 0, 4}}};
In[10]:=
ResourceFunction["SameSpanQ"][list, basis]
Out[10]=

The eighth matrix in the list is a linear combination of the second and seventh vectors:

In[11]:=
RowReduce[Transpose[Flatten /@ list]] // MatrixForm
Out[11]=

Check:

In[12]:=
{{-7, 6, 6, 0}, {4, 2, 0, 4}} == 2 {{-2, 3, 3, 0}, {2, 1, 0, 2}} - 3 {{1, 0, 0, 0}, {0, 0, 0, 0}}
Out[12]=

Function spaces (4) 

Two lists of polynomials that determine the same subspace:

In[13]:=
ResourceFunction[ "SameSpanQ"][{1 - x^2, x - x^3, 1 - x^4}, {-1 + x^2, x - x^3, x^2 - x^4}, x]
Out[13]=

The Legendre polynomials of degree at most n span the same subspace as the space of polynomials of degree at most n:

In[14]:=
ResourceFunction["SameSpanQ"][Table[LegendreP[k, x], {k, 0, 4}], Table[x^k, {k, 0, 4}], x]
Out[14]=

Two lists of trigonometric functions that span the same subspace:

In[15]:=
list1 = Table[Cos[j t], {j, 0, 4}]; list2 = Table[Cos[t]^j, {j, 0, 4}]; ResourceFunction["SameSpanQ"][list1, list2, t]
Out[16]=

Two lists of exponential, trigonometric and hyperbolic functions that span the same subspace:

In[17]:=
ResourceFunction[ "SameSpanQ"][{Cosh[x], Sinh[x], Cos[2 x], Cos[x]^2}, {Exp[x], Exp[-x], Cos[2 x], 1}, x]
Out[17]=

Publisher

Dennis M Schneider

Version History

  • 1.0.0 – 23 September 2019

Related Resources

License Information