Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute properties of the line normal (perpendicular) to a given line and passing through a given point
ResourceFunction["NormalLineThrough"][expr,{x,a},{y,b}] returns an Association of properties for the line passing through the point {x,y}={a,b} and normal to expr, a linear function in x. | |
ResourceFunction["NormalLineThrough"][expr,{x,a},{y,b},prop] returns the normal line property prop. |
| "SlopeInterceptEquation" | equation of the normal line in slope-intercept form |
| "StandardFormEquation" | equation of the normal line in standard form |
| "PointSlopeEquation" | equation of the normal line in point-slope form |
| "Slope" | slope of the normal line |
| "HorizontalIntercept" | horizontal intercept of the normal line |
| "VerticalIntercept" | vertical intercept of the normal line |
| "Plot" | plot of the normal line |
| All | Association of all allowed properties |
Get the point-slope equation of a line normal to y=3x/2+4 that passes through the point (x,y)=(1,-1):
| In[1]:= |
| Out[1]= |
Visualize this result:
| In[2]:= |
| Out[2]= | 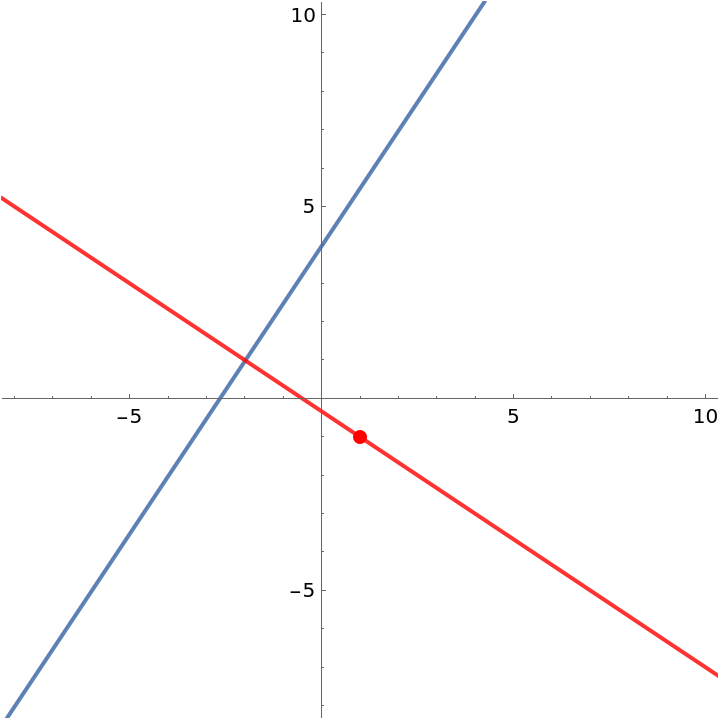 |
Compute the slope of this line:
| In[3]:= |
| Out[3]= |
Compute the horizontal intercept of this line:
| In[4]:= |
| Out[4]= |
Get the standard form equation of this line:
| In[5]:= |
| Out[5]= |
Get an Association of properties of a line normal to y=-x/2+4 that passes through the point (x,y)=(3/5,6/7):
| In[6]:= |
| Out[6]= | 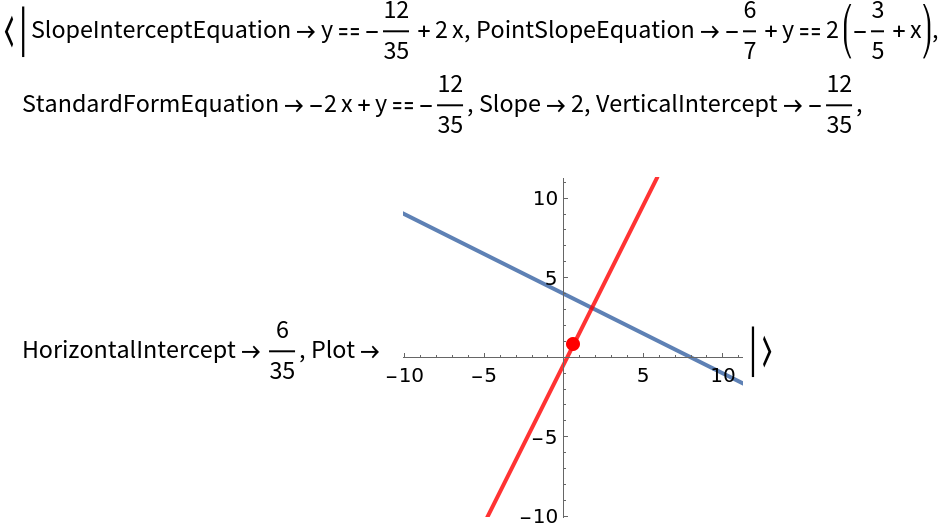 |
Get just the slope-intercept equation of this line:
| In[7]:= |
| Out[7]= |
The first argument to NormalLineThrough must be a linear function of x:
| In[8]:= |
| Out[8]= |
This work is licensed under a Creative Commons Attribution 4.0 International License