Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the catacaustic of a curve at infinity
ResourceFunction["InfiniteCatacausticCurve"][c,θ,t] gives an equation for the catacaustic at infinity of a curve c specified parametrically with respect to a direction angle θ in terms of the variable t. |
The catacaustic at infinity for a parabola, with rays perpendicular to the parabola's axis:
| In[1]:= |
| Out[1]= |
Plot the parabola and the catacaustic (Tschirnhausen cubic) together:
| In[2]:= | ![ParametricPlot[{{t^2, 2 t}, ResourceFunction["InfiniteCatacausticCurve"][{t^2, 2 t}, \[Pi]/2, t]} // Evaluate, {t, -5/2, 5/2}]](https://www.wolframcloud.com/obj/resourcesystem/images/b7e/b7e6acfc-6d7d-49f0-a43c-7b37a1d2d720/3703bd5963758fd7.png) |
| Out[2]= | 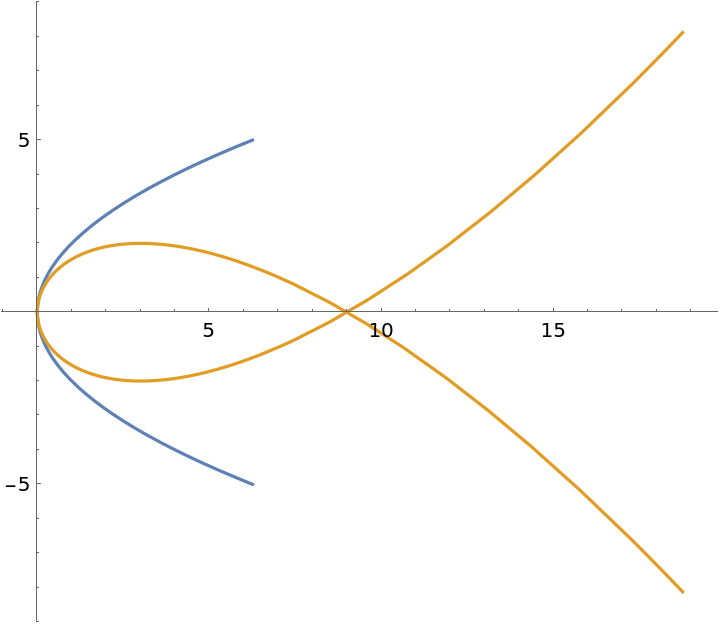 |
The catacaustic at infinity for a circle:
| In[3]:= |
| Out[3]= |
Plot the circle and the catacaustic (nephroid) together:
| In[4]:= | ![ParametricPlot[{{Cos[t], Sin[t]}, ResourceFunction["InfiniteCatacausticCurve"][{Cos[t], Sin[t]}, 0, t]} // Evaluate, {t, 0, 2 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b7e/b7e6acfc-6d7d-49f0-a43c-7b37a1d2d720/55d0113e9657898e.png) |
| Out[4]= | 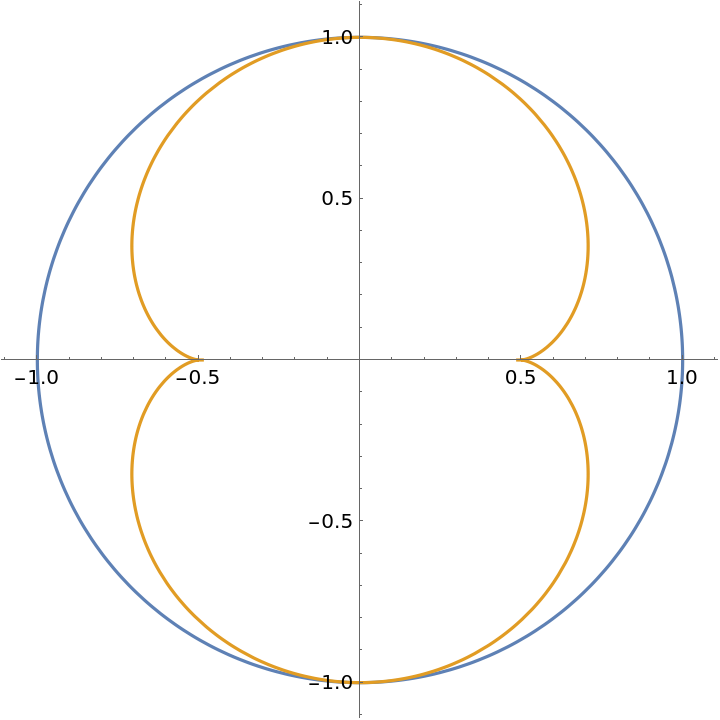 |
Parametric equations for a deltoid:
| In[5]:= |
| Out[5]= |
Demonstrate the effect of changing θ in InfiniteCatacausticCurve:
| In[6]:= | ![Manipulate[
ParametricPlot[
Evaluate[{del[t], ResourceFunction["InfiniteCatacausticCurve"][del[t], \[Theta], t]}], {t, 0, 2 \[Pi]}, PlotRange -> 2], {\[Theta], 0, \[Pi]}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/b7e/b7e6acfc-6d7d-49f0-a43c-7b37a1d2d720/5943e094943c6fcf.png) |
| Out[6]= | 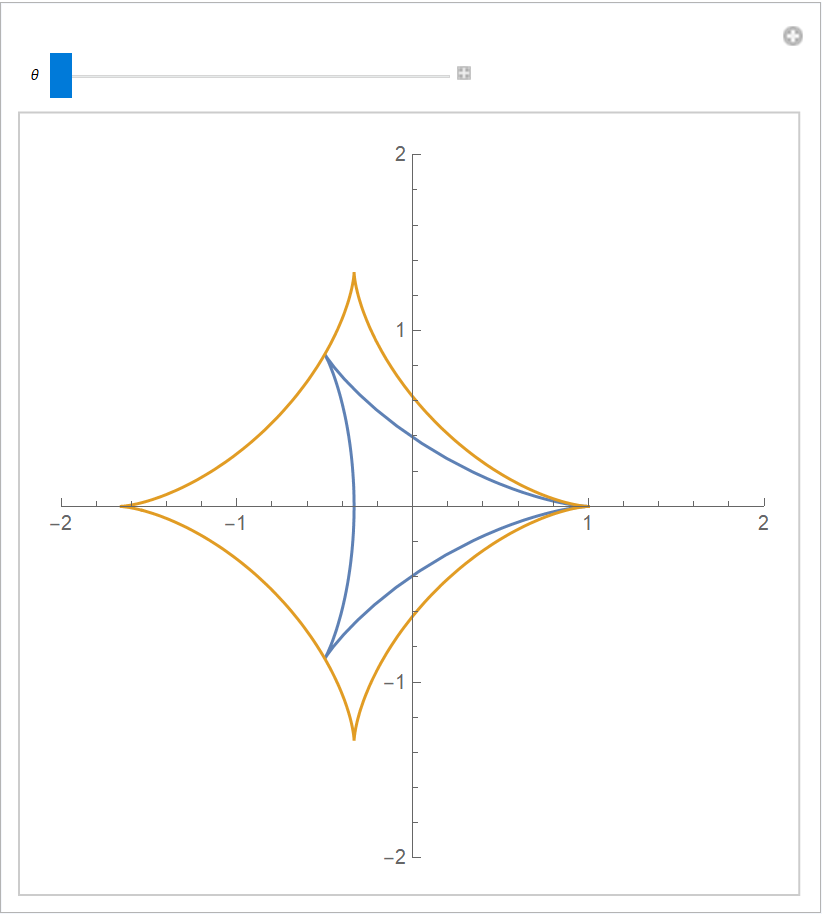 |
This work is licensed under a Creative Commons Attribution 4.0 International License