Basic Examples (2) 

Trace each step in an evaluation:

In[1]:=

Out[1]=

Trace only the computations with head Times:

In[2]:=

Out[2]=

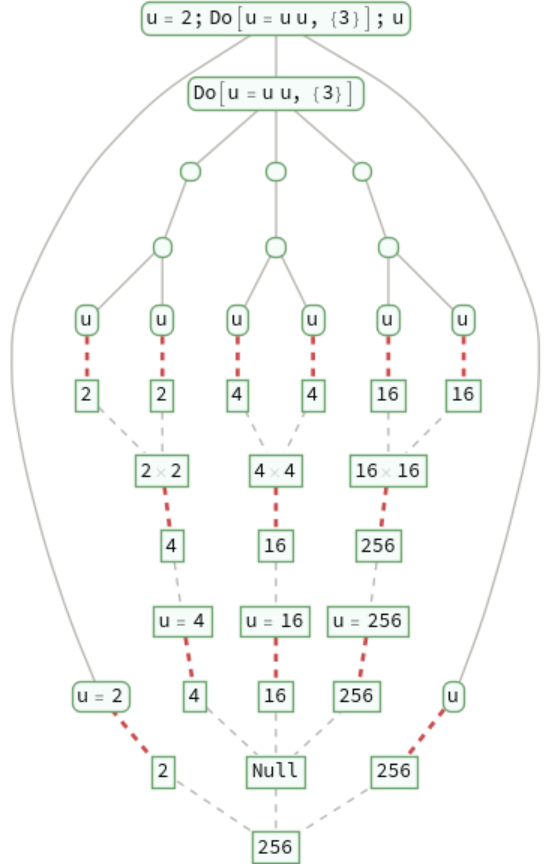
Scope (10) 

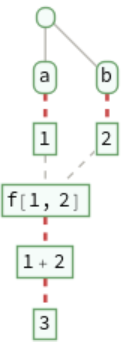
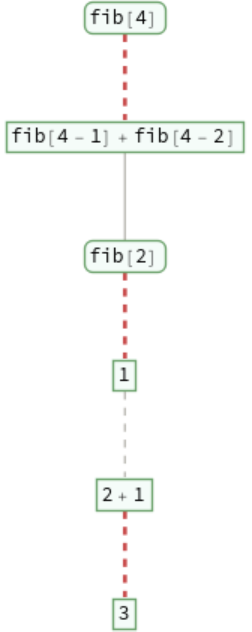
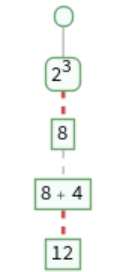
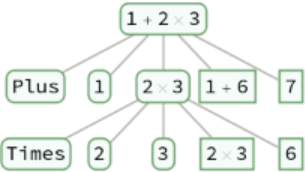
Trace an empty evaluation chain:

In[3]:=

Out[3]=

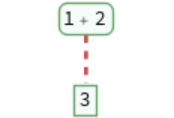
Trace a single step evaluation:

In[4]:=

Out[4]=

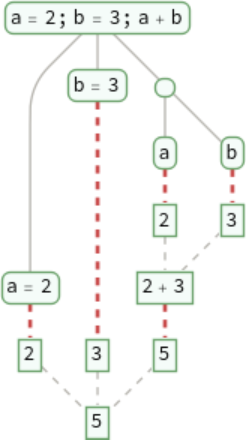
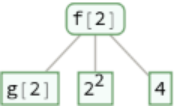
Trace each branch in an evaluation:

In[5]:=

Out[5]=

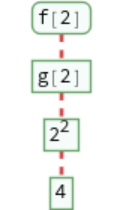
Trace evaluations given by definitions:

In[6]:=

In[7]:=

Out[7]=

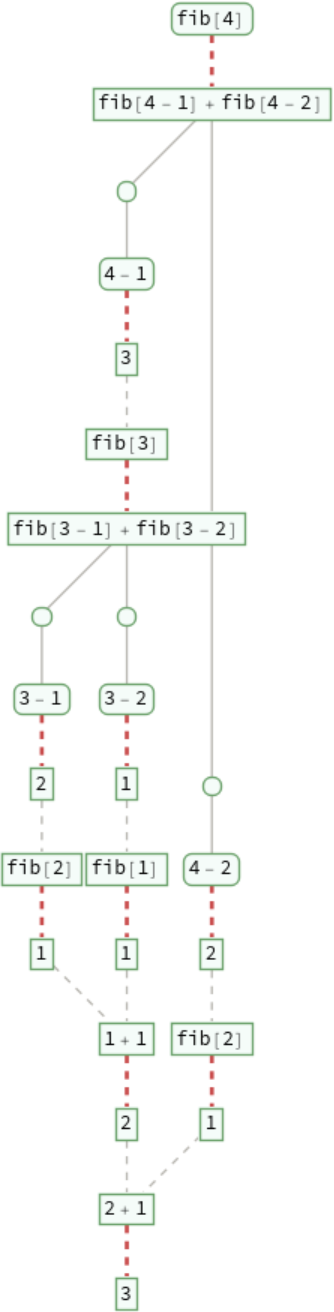
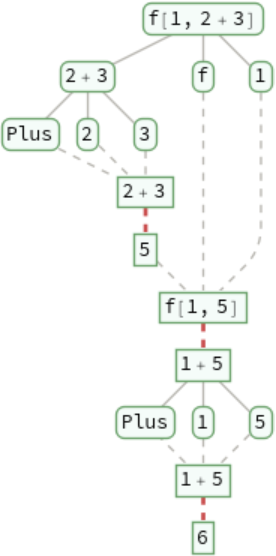
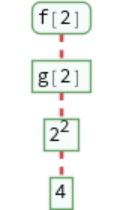
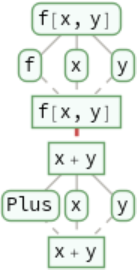
Trace each step in an evaluation:

In[8]:=

Out[8]=

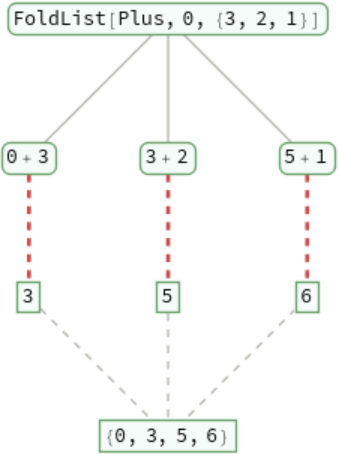
Trace the operation of FoldList:

In[9]:=

Out[9]=

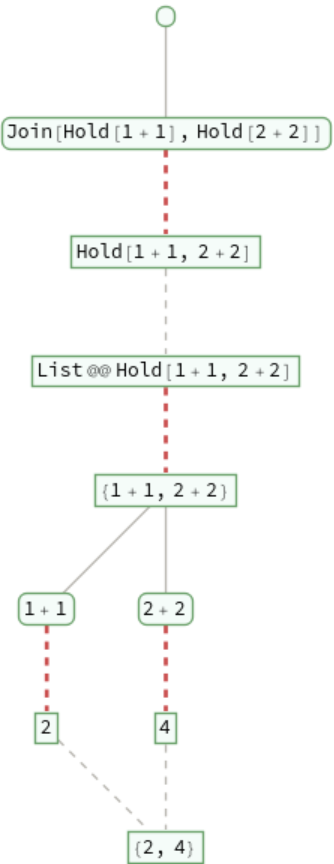
Trace the steps in a non-standard evaluation:

In[10]:=

Out[10]=

Trace each step in an evaluation:

In[11]:=

Out[11]=

Include only those expressions that match _Plus:

In[12]:=

Out[12]=

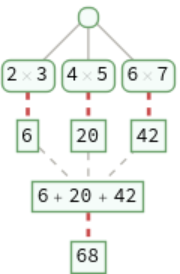
Trace the computations with head Plus:

In[13]:=

Out[13]=

Apply a transformation rule to expressions that match a pattern:

In[14]:=

In[15]:=

Out[15]=

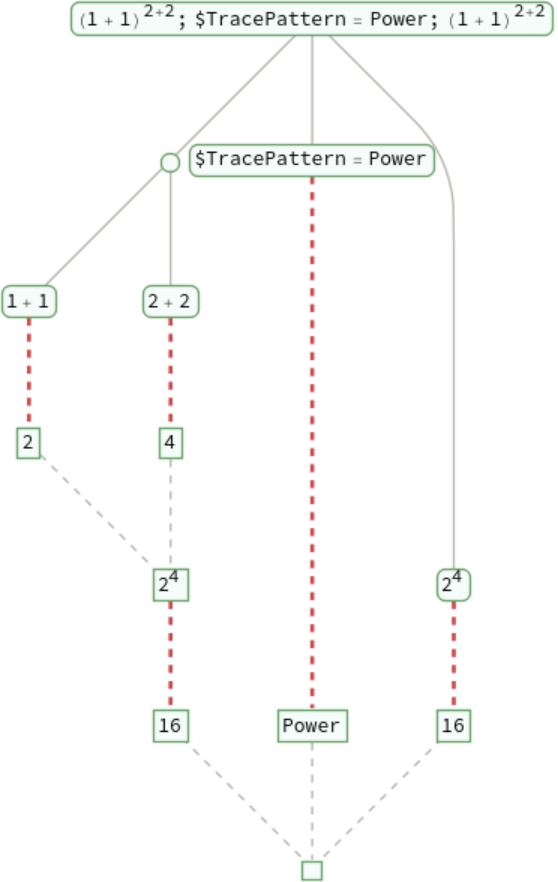
Modify the setting for the form argument during the execution of TraceGraph[expr,form] by resetting the value of the global variable $TracePattern:

In[16]:=

Out[16]=

Options (23) 

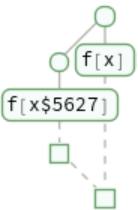
MatchLocalNames (2) 

By default, symbols such as x match symbols with local names of the form x$nnn:

In[17]:=

In[18]:=

Out[18]=

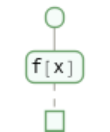
With MatchLocalNames→False, only an explicit match of x will show up:

In[19]:=

Out[19]=

TraceAbove (4) 

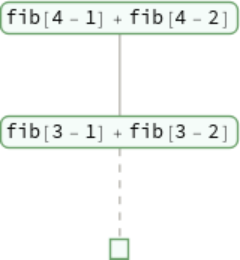
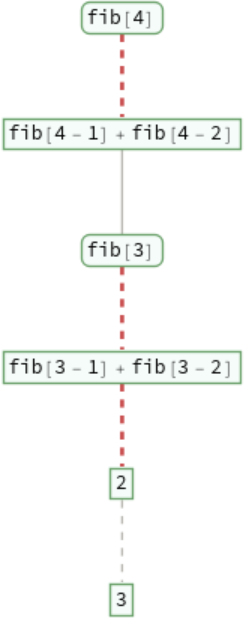
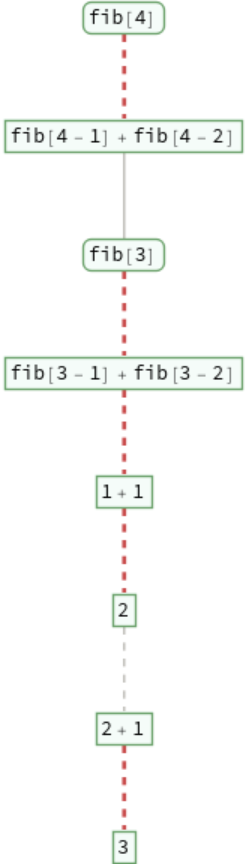
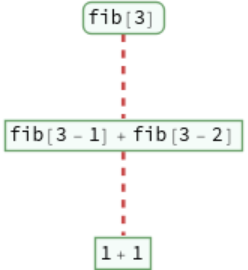
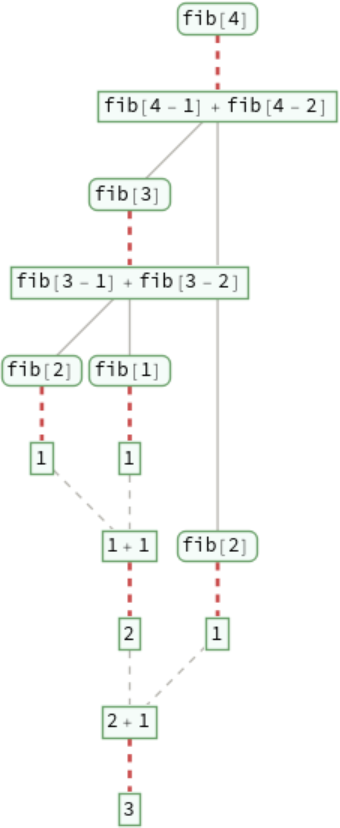
A recursive definition for finding Fibonacci numbers:

In[20]:=

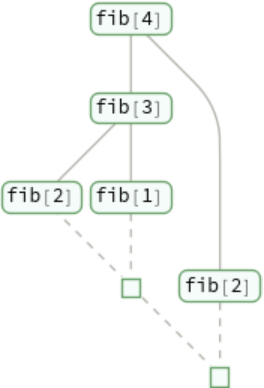
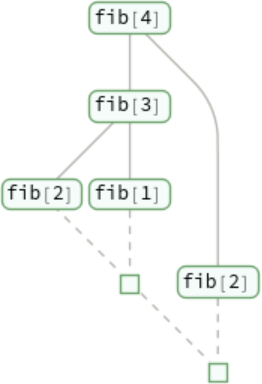
Show only what sums of fib are encountered:

In[21]:=

Out[21]=

Show the beginning of the evaluation chain that leads to each sum of fib:

In[22]:=

Out[22]=

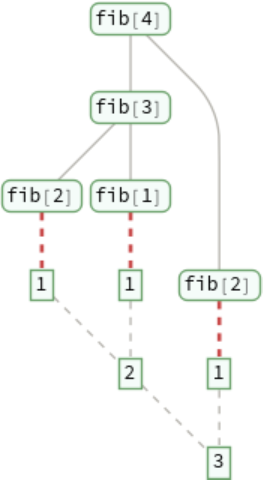
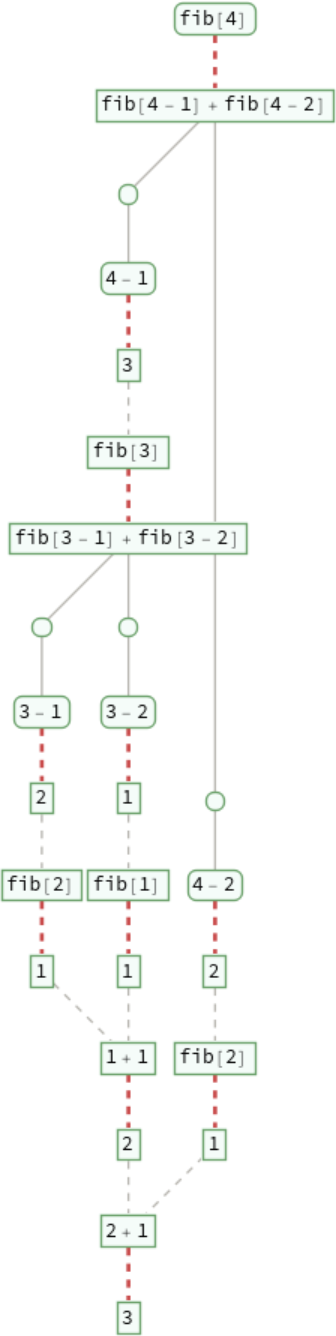
Show the entire evaluation chain that leads to each sum of fib:

In[23]:=

Out[23]=

TraceBackward (4) 

A recursive definition for finding Fibonacci numbers:

In[24]:=

Show only what additions of positive integers are required:

In[25]:=

Out[25]=

Show the beginning of the evaluation chain that leads to each addition:

In[26]:=

Out[26]=

Show all intermediate evaluations that led to each addition:

In[27]:=

Out[27]=

TraceDepth (3) 

A recursive definition for finding Fibonacci numbers:

In[28]:=

Trace only evaluations through depth 3:

In[29]:=

Out[29]=

Trace all evaluations:

In[30]:=

Out[30]=

TraceForward (4) 

A recursive definition for finding Fibonacci numbers:

In[31]:=

Show only what evaluations of fib are encountered:

In[32]:=

Out[32]=

Show only the evaluations of fib and the results:

In[33]:=

Out[33]=

Show all intermediate evaluations between calls of fib and the result:

In[34]:=

Out[34]=

TraceOff (2) 

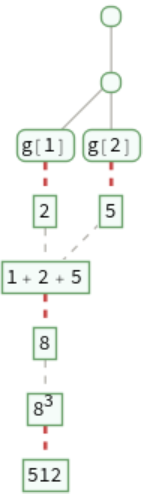
Trace evaluation of an expression that evaluates a function g:

In[35]:=

In[36]:=

Out[36]=

Omit evaluations required to get the values of g:

In[37]:=

Out[37]=

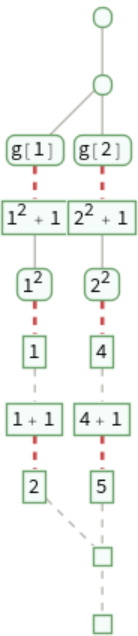
TraceOn (2) 

Trace evaluation of an expression that evaluates a function g:

In[38]:=

In[39]:=

Out[39]=

Trace only evaluation inside of g:

In[40]:=

Out[40]=

TraceOriginal (2) 

Trace evaluation of an expression showing evaluation chains for expressions that change:

In[41]:=

Out[41]=

Show evaluation chains even for expressions that do not change:

In[42]:=

Out[42]=

Applications (5) 

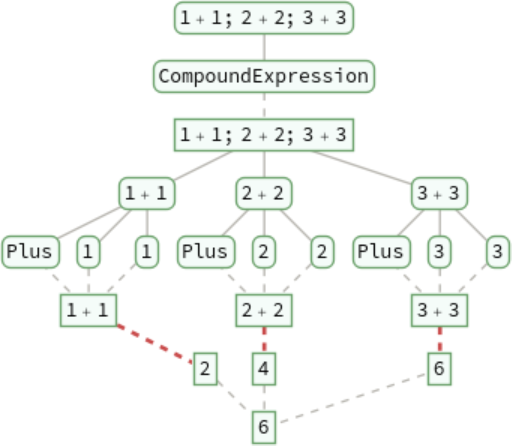
Trace the evaluation of control structures such as CompoundExpression:

In[43]:=

Out[43]=

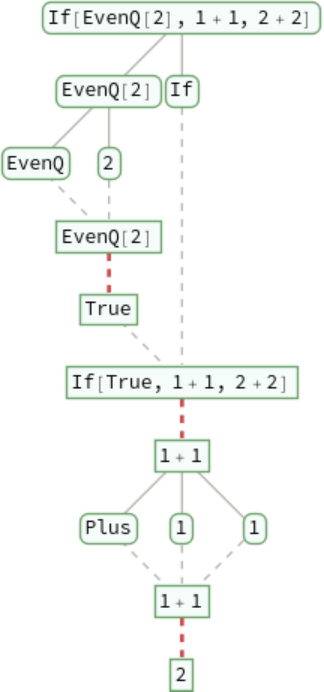
Trace the evaluation of conditionals such as If:

In[44]:=

Out[44]=

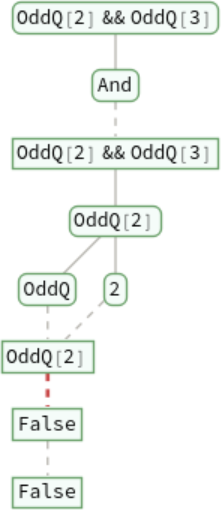
Trace the evaluation of logical operations such as And:

In[45]:=

Out[45]=

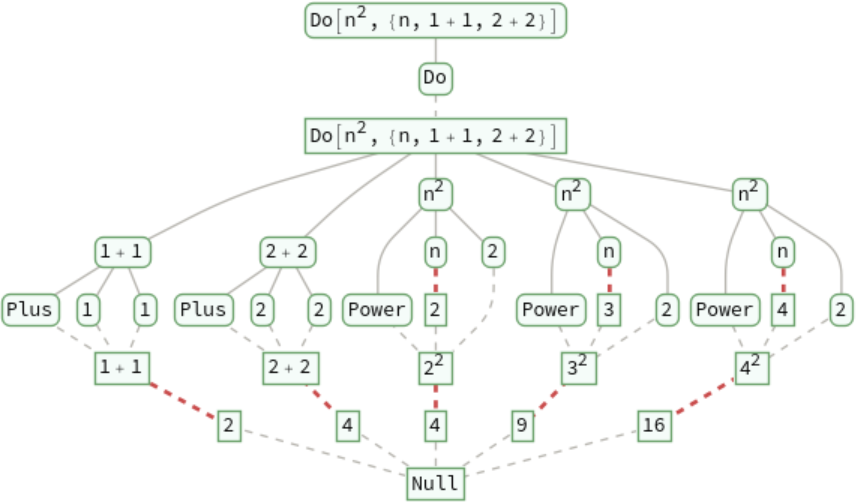
Trace the evaluation of iteration functions such as Do:

In[46]:=

Out[46]=

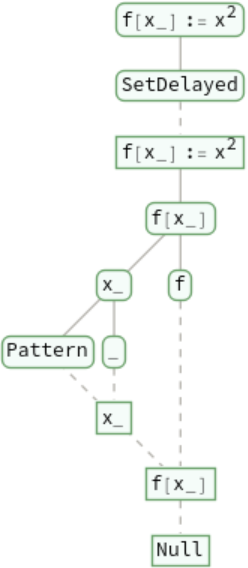
Trace the evaluation of assignments such as SetDelayed:

In[47]:=

Out[47]=

Properties and Relations (8) 

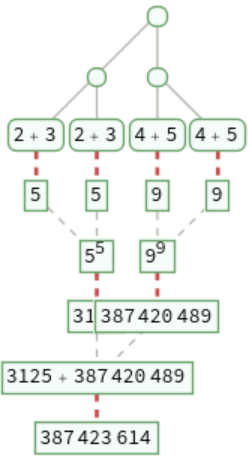
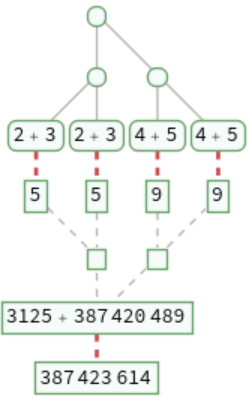
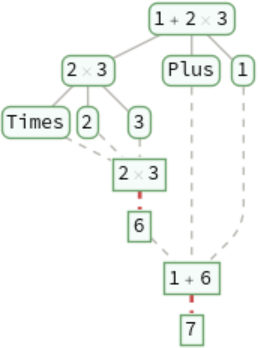
TraceGraph[expr] traces each step in the evaluation of expr:

In[48]:=

In[49]:=

Out[49]=

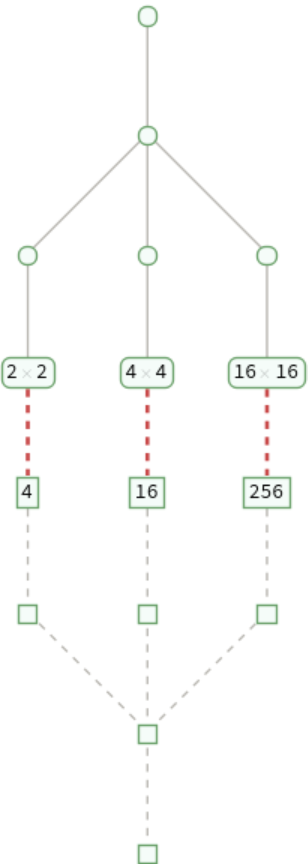
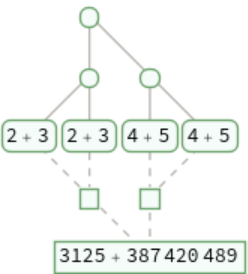
TraceGraph[expr,form] includes only those expressions that match form:

In[50]:=

Out[50]=

This corresponds to deleting all expressions that do not match form, then deleting empty evaluation chains:

In[51]:=

Out[51]=

In[52]:=

Out[52]=

In[53]:=

Out[53]=

In[54]:=

Out[54]=

TraceGraph gives a graph with vertices of the form Trees`TraceNode[HoldForm[expr],pos]:

In[55]:=

Out[55]=

In[56]:=

Out[56]=

TraceGraph uses highlighted dashed edges for iteration:

In[57]:=

In[58]:=

Out[58]=

The children given by TraceTree correspond to subsequent iterations in the reevaluation of expressions:

In[59]:=

Out[10]=

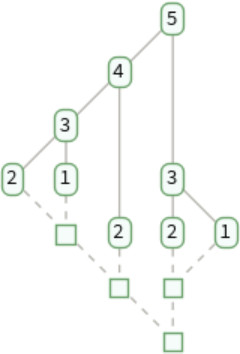
TraceGraph uses solid and dashed edges for increasing and decreasing recursion levels, respectively:

In[60]:=

Out[60]=

The levels given by TraceTree correspond to the recursion levels of subsidiary evaluations:

In[61]:=

Out[11]=

Each iteration in the reevaluation of an expression at recursion level n is represented as Trees`TraceNode[expr,{i₁,…,i_n}]:

In[62]:=

In[63]:=

Out[63]=

In[64]:=

Out[64]=

In[65]:=

Out[65]=

The result of recursion at level n is represented as Trees`TraceNode[expr,{i₁,…,i_n-1}]:

In[66]:=

Out[66]=

In[67]:=

Out[67]=

In[68]:=

Out[68]=

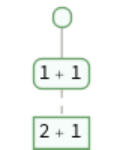
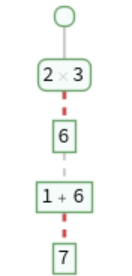
Trees`TraceNode[Null,{…,1}] represents the first node in an evaluation chain when the first expression is not included:

In[69]:=

Out[69]=

In[70]:=

Out[70]=

In[71]:=

Out[71]=

Trees`TraceNode[Null,{…,-1}] represents the last node in evaluation chain when the last expression is not included:

In[72]:=

Out[72]=

In[73]:=

Out[73]=

In[74]:=

Out[74]=