Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Chamfer a given polyhedron
ResourceFunction["ChamferedPolyhedron"][poly] gives the chamfered polyhedron of poly by chamfering all edges. | |
ResourceFunction["ChamferedPolyhedron"][poly,l] chamfers the polyhedron poly by a length ratio l at its edges. |
Chamfer a dodecahedron:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 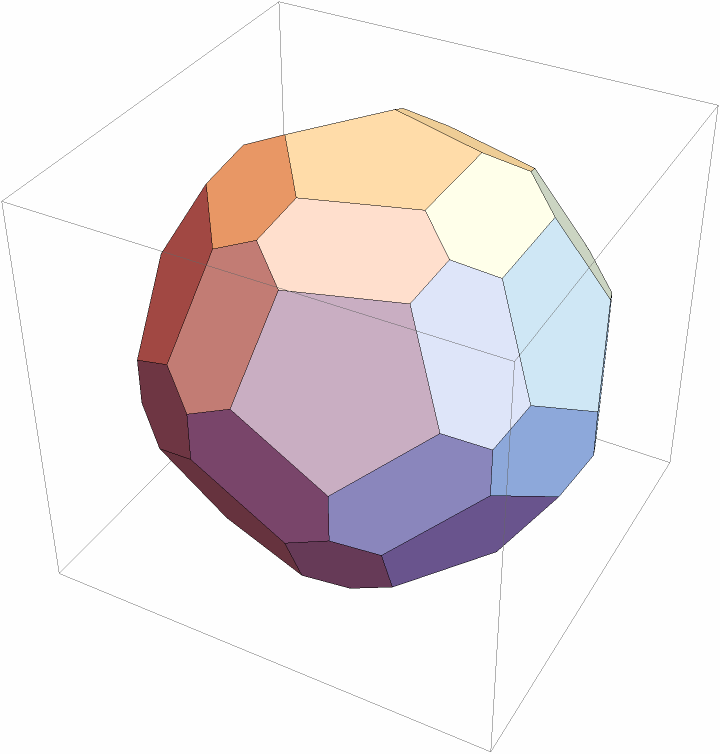 |
ChamferedPolyhedron works on polyhedra:
| In[3]:= |
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= | 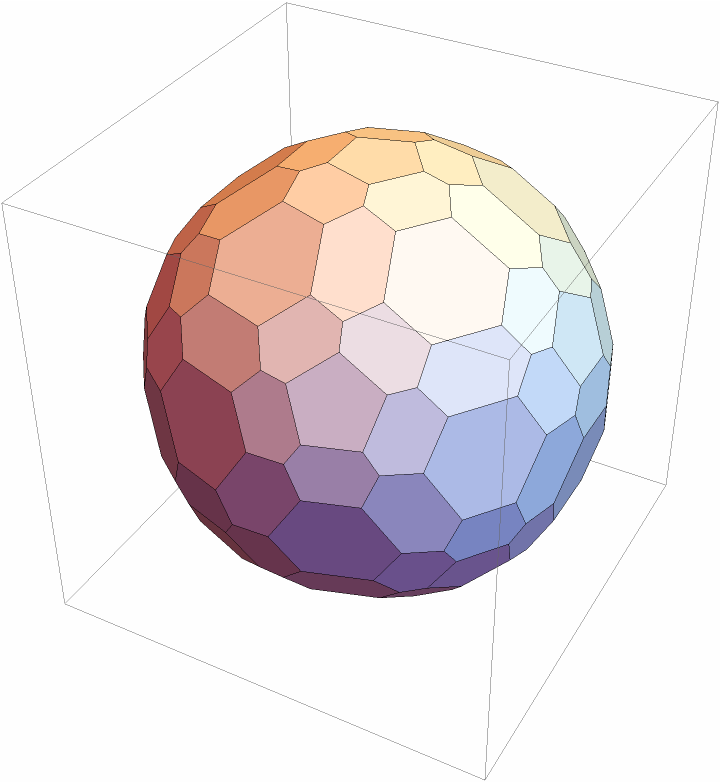 |
Chamfer the polyhedron by different length ratios:
| In[6]:= |
| In[7]:= |
| Out[7]= | 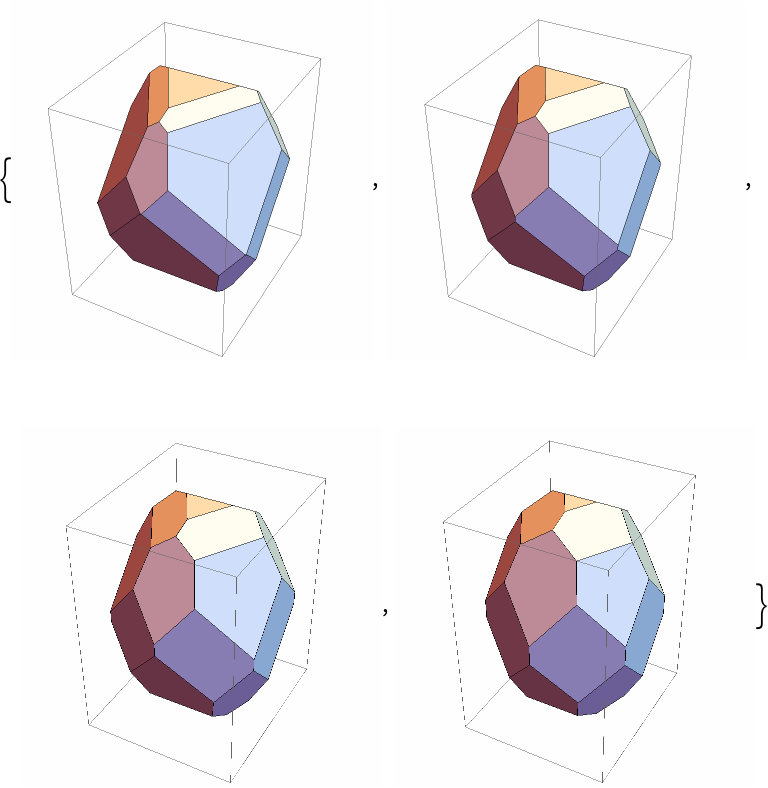 |
ChamferedPolyhedron transforms edges, while BeveledPolyhedron transforms edges and vertices:
| In[8]:= | ![With[{\[ScriptCapitalP] = Icosahedron[]}, GraphicsRow[{Graphics3D[\[ScriptCapitalP], PlotLabel -> "original"], Graphics3D[
ResourceFunction["ChamferedPolyhedron"][\[ScriptCapitalP]], PlotLabel -> "chamfered"], Graphics3D[BeveledPolyhedron[\[ScriptCapitalP]], PlotLabel -> "beveled"]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/ac3/ac344547-a52c-471e-8374-e1d8ebec87d1/5dd1d0eb9f7e71f6.png) |
| Out[8]= | 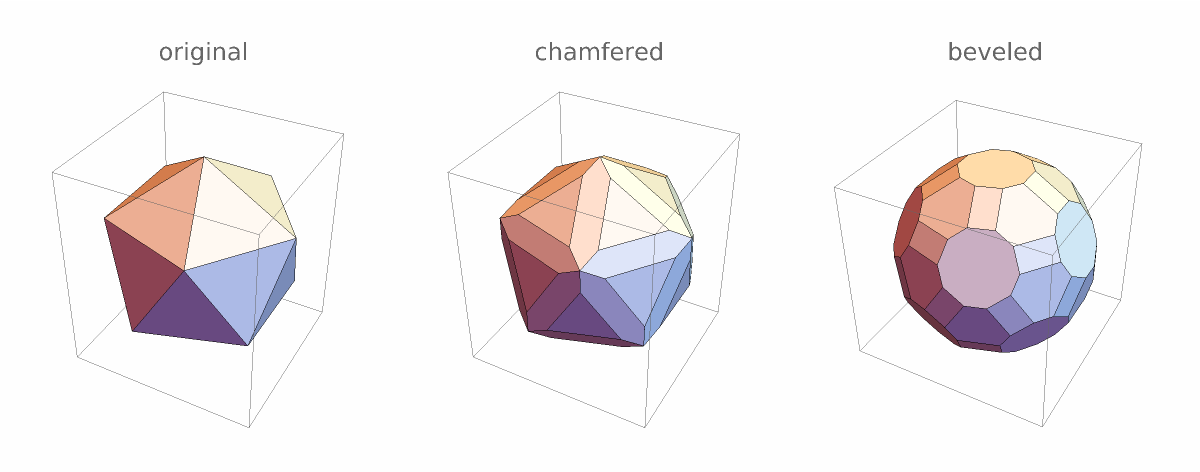 |
ChamferedPolyhedron only supports simple polyhedra:
| In[9]:= | ![\[ScriptCapitalP] = Polyhedron[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, {1, 0, 0}, {2, 0, 0}, {1, 1, 0}, {1, 0, 1}}, {{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}, {5, 6, 7}, {5, 6, 8}, {6, 7, 8}, {5, 7,
8}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ac3/ac344547-a52c-471e-8374-e1d8ebec87d1/6e6cf37ebb68cf19.png) |
| Out[9]= |
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
Equilateral chamfered polyhedra based on Platonic solids:
| In[12]:= | ![Grid[MapThread[{f, r} |-> {Graphics3D[f[1], Boxed -> False], \!\(\*
GraphicsBox[
{GrayLevel[0.7], PolygonBox[{{0, 0}, {-0.5, 0.5}, {-0.5, 0.25}, {-1, 0.25}, {-1, -0.25}, {-0.5, -0.25}, {-0.5, -0.5}}]},
ImageSize->25]\), Graphics3D[ResourceFunction["ChamferedPolyhedron"][f[1], r], Boxed -> False]}, {{Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron}, {(18 - 3 Sqrt[2])/17, (16 - 4 Sqrt[3])/13, (
6 - Sqrt[6])/5, 2/41 (30 + 4 Sqrt[5] - Sqrt[365 + 158 Sqrt[5]]), 6/941 (186 + 12 Sqrt[5] - Sqrt[6145 + 2582 Sqrt[5]])}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/ac3/ac344547-a52c-471e-8374-e1d8ebec87d1/67e078b593126a1c.png) |
| Out[12]= | 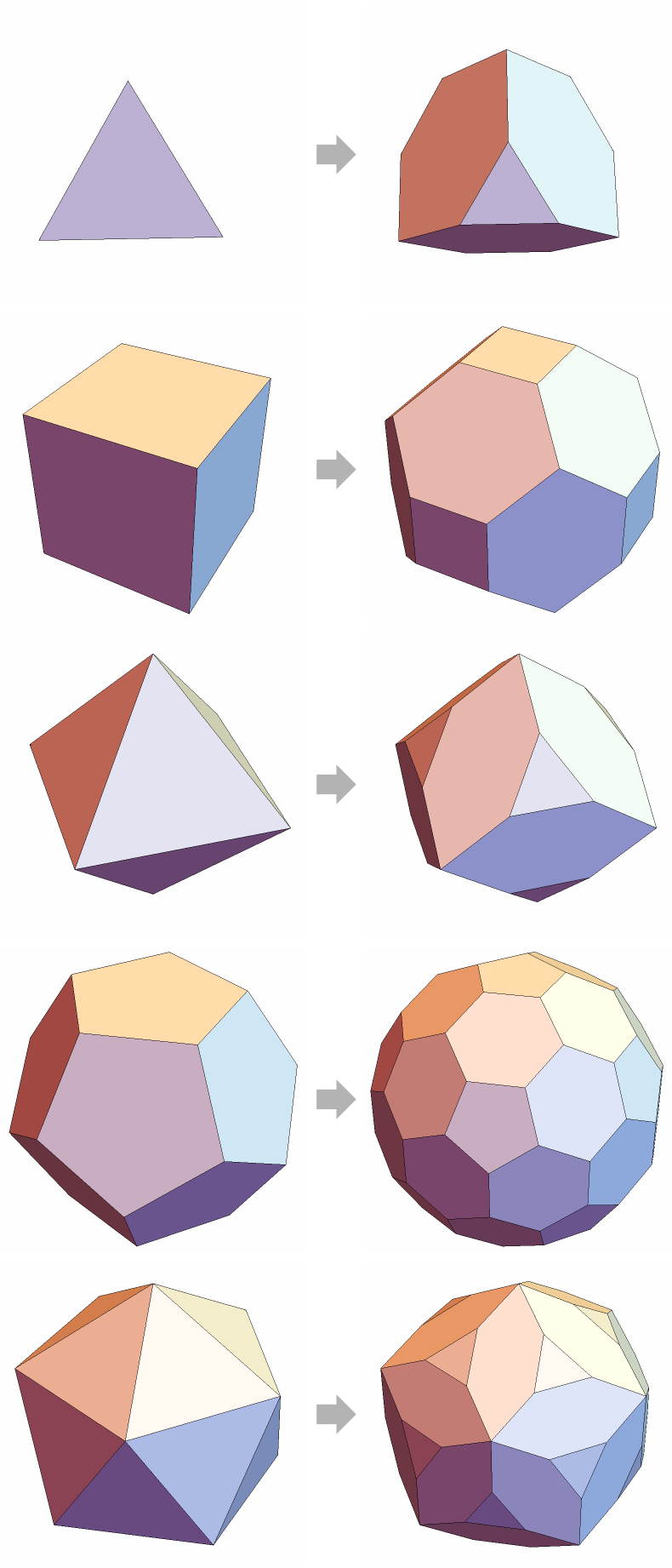 |
Show the relationship between a polyhedron and its chamfered version:
| In[13]:= | ![Manipulate[
Graphics3D[{{Opacity[1/2], Dodecahedron[]}, ResourceFunction["ChamferedPolyhedron"][Dodecahedron[], r]}], {{r, 0.5}, 0.001, 0.999}]](https://www.wolframcloud.com/obj/resourcesystem/images/ac3/ac344547-a52c-471e-8374-e1d8ebec87d1/34b2248e8af81ebf.png) |
| Out[13]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License