Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Give a simple undirected graph a proper edge coloring using at most one color more than necessary
ResourceFunction["VizingEdgeColoring"][gra] finds a proper edge coloring of the simple undirected graph gra using at most one more color than necessary. |
Define a graph and find a proper edge coloring:
| In[1]:= |
| Out[2]= |
Define a function for plotting a proper edge coloring:
| In[3]:= | ![colorAssociation[graph_] := With[{colors = Range[Max[VertexDegree[graph]] + 1]}, AssociationMap[Function[color, Hue[color/Length[colors]]], colors]]
edgeColoringPlot[graph_, coloring_] := SetProperty[
graph, {VertexLabels -> "Name", EdgeLabels -> Normal[coloring], EdgeStyle -> Normal[Map[colorAssociation[graph], coloring]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/01e/01e42e7b-5e97-4779-a1bc-aa0ce7f73dca/1f51b1ae71748497.png) |
Plot the proper edge coloring:
| In[4]:= |
| Out[4]= | 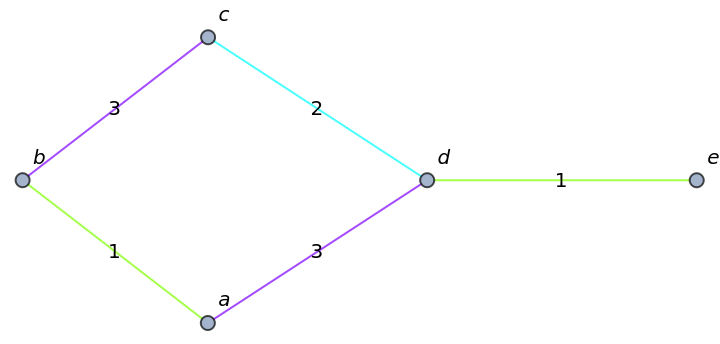 |
Find a proper edge coloring for the Petersen graph:
| In[5]:= |
| Out[6]= |
Plot it:
| In[7]:= |
| Out[7]= | 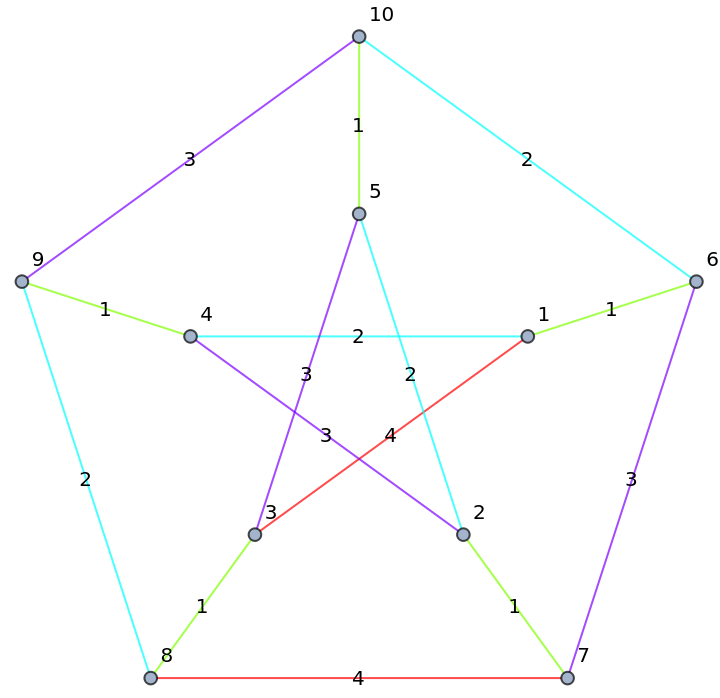 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License