Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Determine if the span of one list of vectors is contained in the span of a second list of vectors
ResourceFunction["VectorSubspaceQ"][list1,list2] tests whether the span of the first list of vectors is contained in the span of the second list of vectors. | |
ResourceFunction["VectorSubspaceQ"][list1,list2,var] performs the same test for lists of functions of var. |
The span of the first list is contained in the span of the second list:
| In[1]:= | ![list1 = {{1, 2, 3, 1}, {1, 2, 4, 2}, {2, 4, 7, 3}};
list2 = {{2, 4, 7, 1}, {0, 0, 2, 2}, {1, 2, 0, 2}};
ResourceFunction["VectorSubspaceQ"][list1, list2]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba14a106-c47f-42f4-b7f5-644ce4af5337/2f2a44072e6d4413.png) |
| Out[1]= |
The span of the second list of vectors is not contained in the span of the first list:
| In[2]:= |
| Out[2]= |
Check:
The span of list1 is contained in the span of list2 since every vector in list1 is a linear combination of vectors in list2:
| In[3]:= |
| Out[9]= |  |
The first and third vectors in list2 are not linear combinations of the vectors in list1:
| In[10]:= |
| Out[16]= |  |
The subspace spanned by the first list of vectors (matrices) is contained in the subspace spanned by the second list:
| In[17]:= | 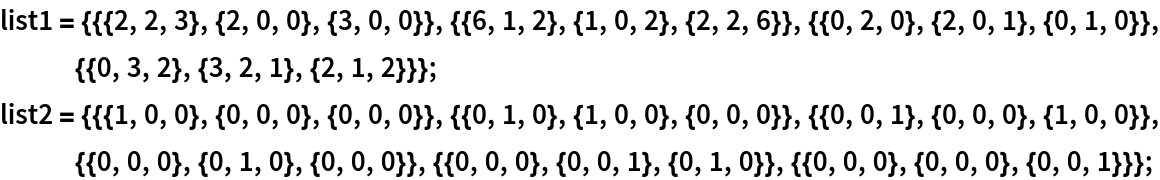 |
| In[18]:= |
| Out[18]= |
However, the two subspaces are not equal:
| In[19]:= |
| Out[19]= |
Confirm by checking with the resource function SameSpanQ:
| In[20]:= |
| Out[20]= |
The span of the first list of trigonometric functions is contained in the span of the second list, as can be verified using trigonometric identities:
| In[21]:= |
| Out[21]= |
But the two subspaces are not equal:
| In[22]:= |
| Out[22]= |
The first function cos(x) is not a linear combination of 1,cos(2x),cos(4x):
| In[23]:= |
| Out[23]= |
But each of the other functions cos2(x),cos4(x),sin4(x) in the first list is a linear combination of the three functions 1,cos(2x),cos(4x):
| In[24]:= |
| Out[24]= |
The even Chebyshev polynomials of the first kind of degree at most 10 form a subspace of the space of all polynomials of degree at most 10:
| In[25]:= |
| Out[25]= |
| In[26]:= |
| Out[26]= |
But the two subspaces are not equal:
| In[27]:= |
| Out[27]= |
Check with the resource function SameSpanQ:
| In[28]:= |
| Out[28]= |
This work is licensed under a Creative Commons Attribution 4.0 International License