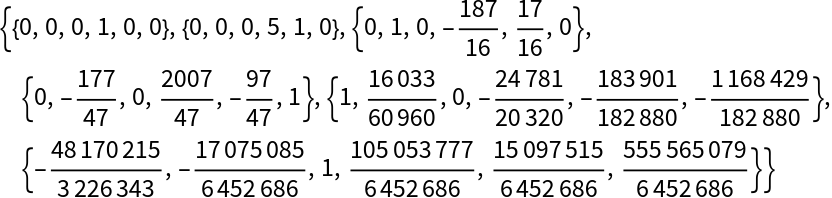Options (2)
Create a random integer matrix:
Compute the upper triangular decomposition:
Now compute an upper triangular decomposition modulo a prime:
Create a random integer matrix:
Compute the full row echelon decomposition {rred,c} such that rred is in reduced row echelon form and c.mat==rred:
Check the result:
Properties and Relations (13)
Create a symmetric positive definite matrix:
Check that it is actually positive definite:
Compute the upper triangular decomposition:
Check that the decomposition is correct, now using the inverse of c and multiplying by u to recover mat:
We can get a different upper triangular factorization using CholeskyDecomposition:
Check the result:
Another factorization with an upper triangular factor is obtained using QRDecomposition:
Check the result:
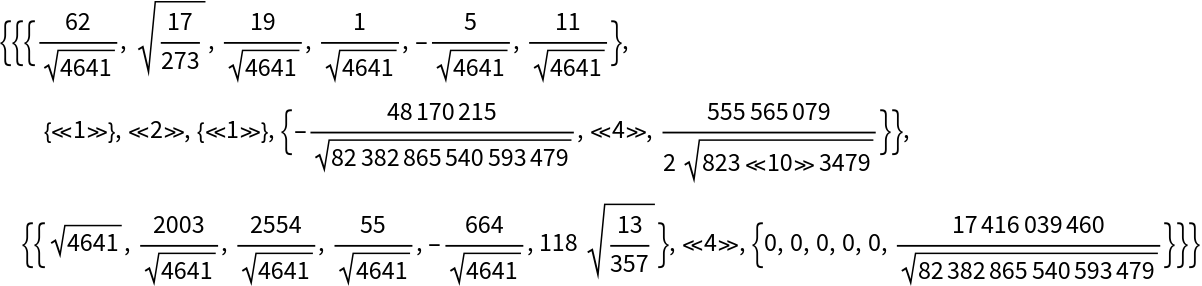
We get yet another triangular factorization of mat using LUDecomposition:
Recover the two triangular factors:
Check that the product of these factors gives mat transformed by the permutation perm used by LUDecomposition:
Use the permutation and lower factor to find the conversion matrix for an upper triangular decomposition:
Check this:
One will notice that of all these factorizations, only UpperTriangularizeMatrix avoids both fractions and radicals.
Possible Issues (2)
If the input matrix is approximate the full echelon form will be computed:
This is different from the exact case:
![cm = CauchyMatrix[{1, 2, 3}, {1, 5, 6}];
ResourceFunction["UpperTriangularDecomposition"][cm] == ResourceFunction["UpperTriangularDecomposition"][Normal@cm] == ResourceFunction["UpperTriangularDecomposition"][SparseArray@cm]](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f291f337-7bb2-49aa-b584-1ba3665a1335/624fcb0aabb194fe.png)
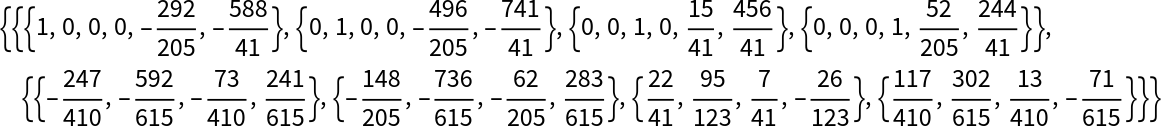
![SeedRandom[1234];
mat0 = RandomInteger[{-10, 10}, {6, 6}];
mat = mat0 + Transpose[mat0] + 80*IdentityMatrix[6]](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f291f337-7bb2-49aa-b584-1ba3665a1335/3bba2aad02215fe3.png)


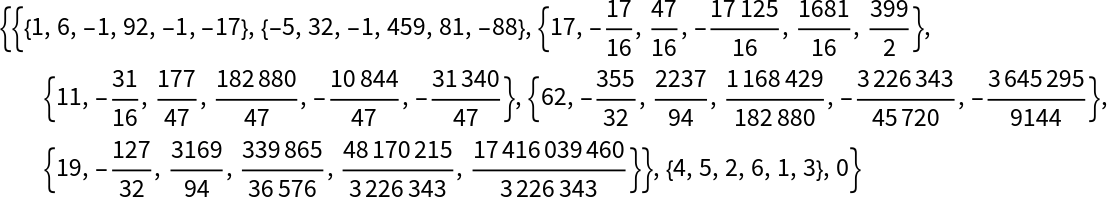
![getL[mat_] := With[{r = Length[mat]}, PadRight[LowerTriangularize[mat, -1], {r, r}, 0] + IdentityMatrix[r]]
{l, u} = {getL[lu], UpperTriangularize[lu]}](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f291f337-7bb2-49aa-b584-1ba3665a1335/7ef85c3669c30e0d.png)