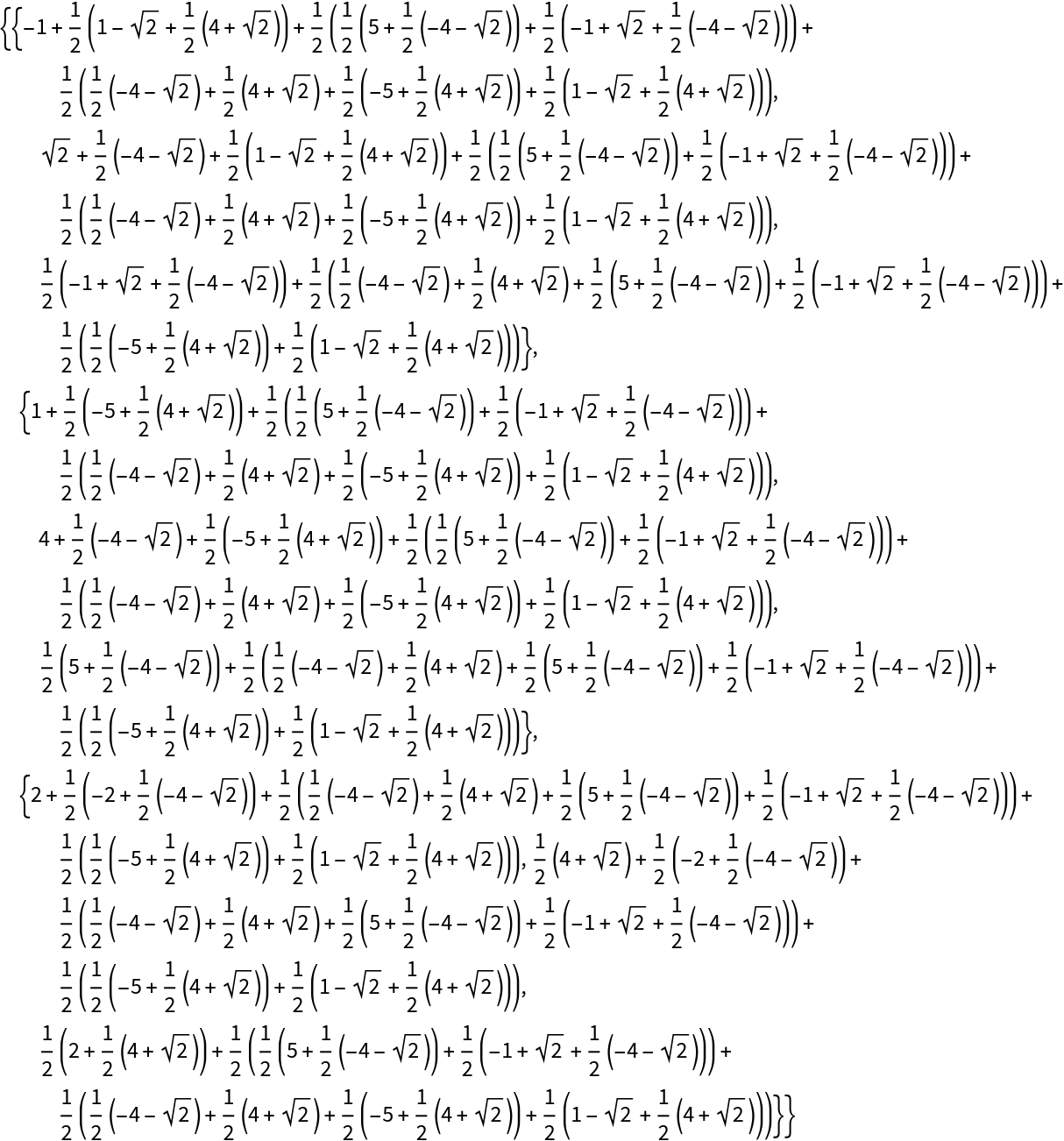Details and Options
Matrix mat has to be numerical.
Median polishing is a robust exploratory data analysis method to find row and column effects in a matrix of data similar to two-way ANOVA. The main idea is that the elements of the matrix are of the form
mi,j=c+xi+yj+ϵi,j. In this model, the
xi are called the
row effects,
yj the
column effects,
c the
overall effect and the
ϵi,j are the residuals. In order to estimate these effects, it is assumed that all of these quantities (except the constant
c) average out to 0 over
i and/or
j. However, since the amount of data is limited, the
Mean is not a good location estimator to use and instead the
Median is used as a more robust alternative. Other location estimators can be specified if necessary.
To estimate c, xi and yj, the algorithm first subtracts the medians from the columns of mat and adds them to the yj and also subtracts the median from the xi vector and adds it to c. Then the algorithm repeats the process for the rows (adding the medians to the xi) and the yj (adding its median to c again). This process is iterated until convergence is reached.
The argument "prop" can either be "Matrix" (default) or "PropertyAssociation".
ResourceFunction["TukeyMedianPolish"] takes the following options:
| "LocationEstimator" | Median | location estimator to use |
| MaxIterations | 100 | maximum number of iterations to use |
| Tolerance | Scaled[10-4] | maximum (scaled) difference between two successive steps before the algorithm terminates |
| "ConvergenceTest" | Automatic | function that tests if convergence has been reached |
| Compiled | False | whether to use function compilation to speed up the computation |
If a custom
"LocationEstimator" is specified, it should behave in the same way as
Median and
Mean when applied to a matrix, meaning that
locEst[matrix] should produce the same result as
locEst/@Transpose[matrix].
If an option value other than
Automatic is specified for
"ConvergenceTest", the
Tolerance option will be ignored. The algorithm will evaluate
sametest[medians,current] after each iteration, with
medians being the median values computed in this step and
current being the current output result if the algorithm stops. When the function returns
True, the algorithm stops.



![With[{mat = RandomVariate[CauchyDistribution[], {5, 6}]},
AssociationMap[
Grid[ResourceFunction["TukeyMedianPolish"][mat, "LocationEstimator" -> #], Dividers -> {-2 -> True, -2 -> True}] &,
{Median, Mean, TrimmedMean[#, 0.2] &, WinsorizedMean[#, 0.2] &}
]
]](https://www.wolframcloud.com/obj/resourcesystem/images/c9e/c9ea50ee-d5b6-4a1c-b9a0-bd9e2ecf219e/2f5c8bc3d8623f52.png)
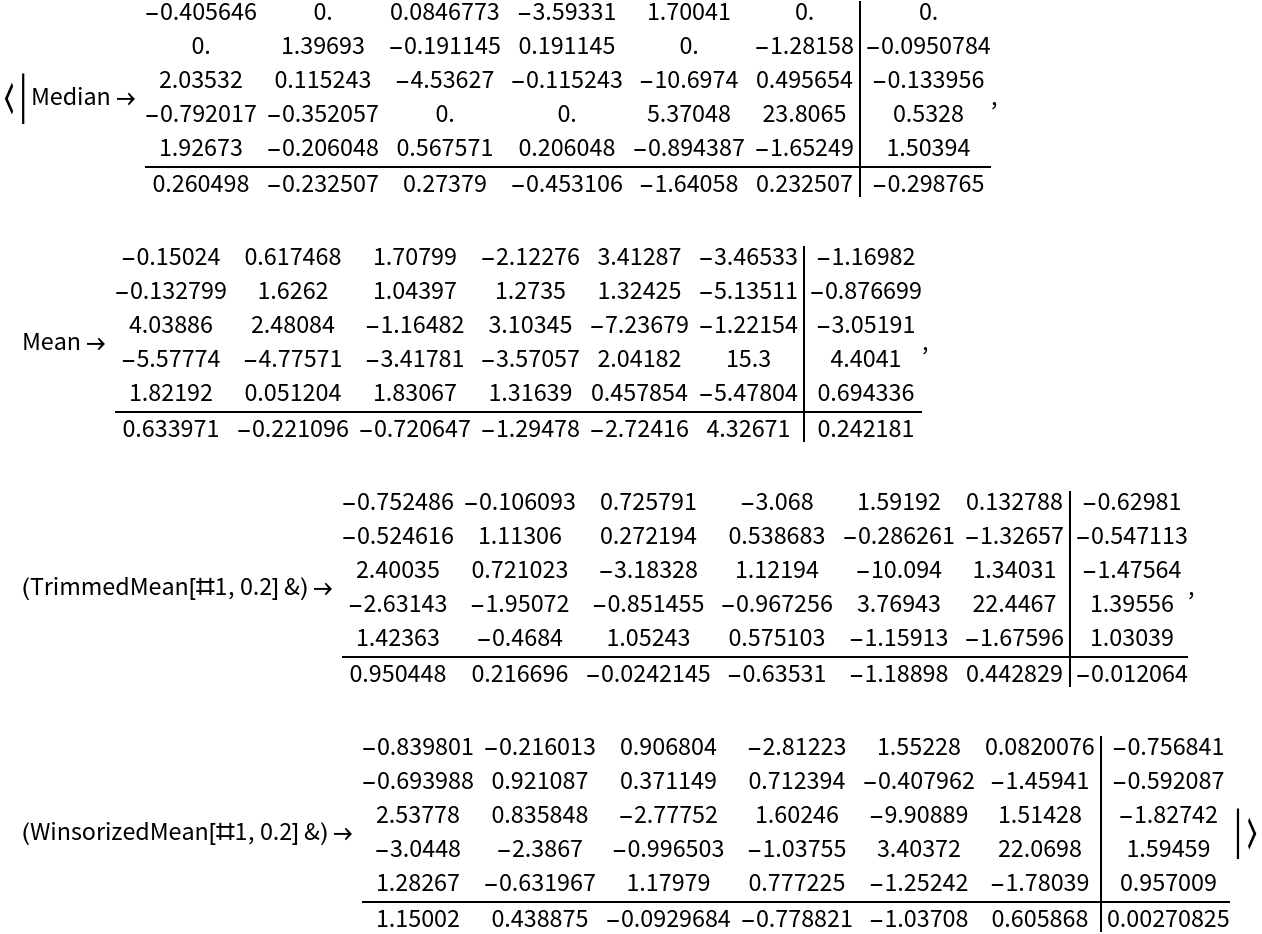
![matrix = RandomReal[100, {4, 6}];
residualsColumn = Column[{
Median@#Residuals, Median /@ #Residuals,
Median @#RowEffects, Median@#ColumnEffects
}] &;
residualsColumn[
ResourceFunction["TukeyMedianPolish"][matrix, "PropertyAssociation"]]](https://www.wolframcloud.com/obj/resourcesystem/images/c9e/c9ea50ee-d5b6-4a1c-b9a0-bd9e2ecf219e/1853c2f72c68c0a4.png)


![matrix = RandomReal[1, {40, 60}];
residualsColumn = Column[{
Max@Abs[Median@#Residuals], Max@Abs[Median /@ #Residuals],
Median @#RowEffects, Median@#ColumnEffects
}] &;
residualsColumn[
ResourceFunction["TukeyMedianPolish"][matrix, "PropertyAssociation", Tolerance -> 10^-10]]](https://www.wolframcloud.com/obj/resourcesystem/images/c9e/c9ea50ee-d5b6-4a1c-b9a0-bd9e2ecf219e/11007265695a00be.png)

![residualsColumn[
ResourceFunction["TukeyMedianPolish"][matrix, "PropertyAssociation", Tolerance -> 10^-10, MaxIterations -> 1000]]](https://www.wolframcloud.com/obj/resourcesystem/images/c9e/c9ea50ee-d5b6-4a1c-b9a0-bd9e2ecf219e/5b626359f45f2207.png)

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/bb818904-03e5-49b2-898d-cdb361ec42e6"]](https://www.wolframcloud.com/obj/resourcesystem/images/c9e/c9ea50ee-d5b6-4a1c-b9a0-bd9e2ecf219e/632b95b8cf81bb90.png)
![Column[{
ResourceFunction["TukeyMedianPolish"][{{1, 2}, {3, 4}}, Compiled -> False],
ResourceFunction["TukeyMedianPolish"][{{1, 2}, {3, 4}}, Compiled -> True]
}]](https://www.wolframcloud.com/obj/resourcesystem/images/c9e/c9ea50ee-d5b6-4a1c-b9a0-bd9e2ecf219e/2456da91e5b49e54.png)