Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a trig series that approximates a list of data
ResourceFunction["TrigApproximateList"][data,var] generates a trig series in var which approximately matches equally spaced data. | |
ResourceFunction["TrigApproximateList"][data,var,n] generates a trig series of n terms in var which approximately matches equally spaced data. | |
ResourceFunction["TrigApproximateList"][{{x1,y1},{x2,y2},…},var,n] generates two trig series of n terms in var which, as a parametric function, approximately matches each column of data. |
Create an approximate formula for a sequence of values based on the discrete Fourier transform of the data:
| In[1]:= |
| Out[2]= | 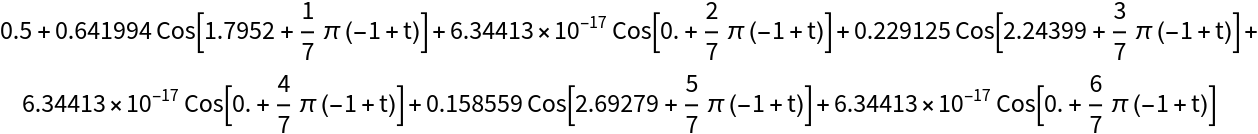 |
| In[3]:= | ![Show[
Plot[f, {t, 1, Length[data]}],
ListPlot[data]]](https://www.wolframcloud.com/obj/resourcesystem/images/4f6/4f6b85c9-469e-48a2-a2fc-8190564ab5f9/624ab3f397c72bd2.png) |
| Out[3]= | 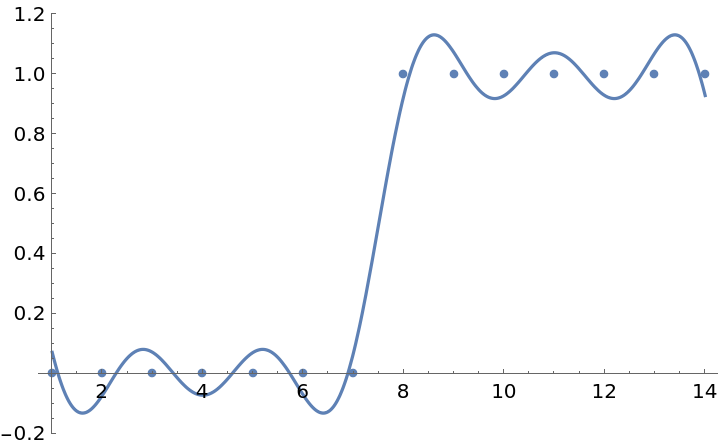 |
A simpler approximation can be created by using only the three most dominant values from the discrete Fourier transform:
| In[4]:= |
| Out[4]= |
| In[5]:= | ![Show[
Plot[f, {t, 1, Length[data]}],
ListPlot[data]]](https://www.wolframcloud.com/obj/resourcesystem/images/4f6/4f6b85c9-469e-48a2-a2fc-8190564ab5f9/71616da88ee7d1ad.png) |
| Out[5]= | 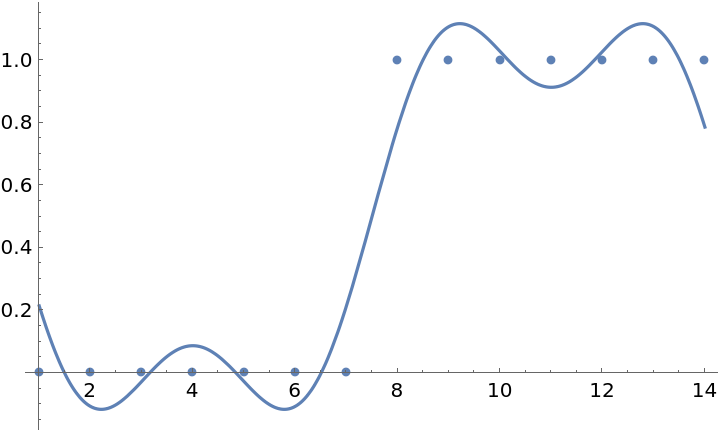 |
For unevenly-spaced data or a path of points in 2D space, TrigApproximateList generates a pair of expressions using a common variable:
| In[6]:= | ![pts = {{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0, 0}};
xfn = Interpolation[Transpose[pts][[1]], InterpolationOrder -> 1];
yfn = Interpolation[Transpose[pts][[2]], InterpolationOrder -> 1];
sqdata = Table[{xfn[t], yfn[t]}, {t, 1, 5, 0.05}];
ListPlot[sqdata]](https://www.wolframcloud.com/obj/resourcesystem/images/4f6/4f6b85c9-469e-48a2-a2fc-8190564ab5f9/20efe8ff92fb68b6.png) |
| Out[10]= |  |
| In[11]:= |
| Out[11]= | 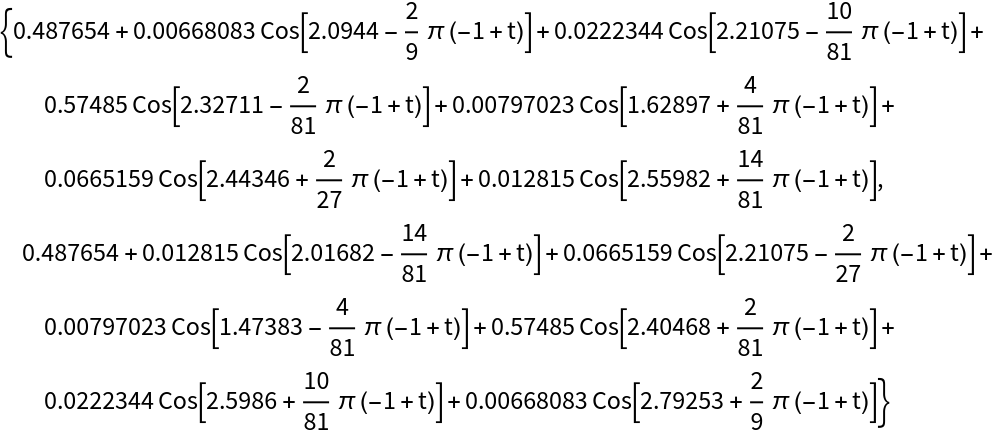 |
The output is appropriate for use within ParametricPlot to generate this approximation to a square:
| In[12]:= |
| Out[12]= |  |
More terms produce more accurate approximations:
| In[13]:= | ![Table[ParametricPlot[
Evaluate[ResourceFunction["TrigApproximateList"][sqdata, t, n]], {t,
0, Length[sqdata]}], {n, 2, 7}]](https://www.wolframcloud.com/obj/resourcesystem/images/4f6/4f6b85c9-469e-48a2-a2fc-8190564ab5f9/555607f6fb22ba22.png) |
| Out[13]= |  |
When the number of terms is not specified, TrigApproximateList uses Length[data]/2 terms:
| In[14]:= |
| Out[14]= |  |
This produces the most accurate approximation possible while still preventing high-frequency over-fitting:
| In[15]:= |
| Out[15]= |  |
The data range is assumed to be from 1 to Length[data]. To change this, use DataRange:
| In[16]:= |
| Out[17]= | 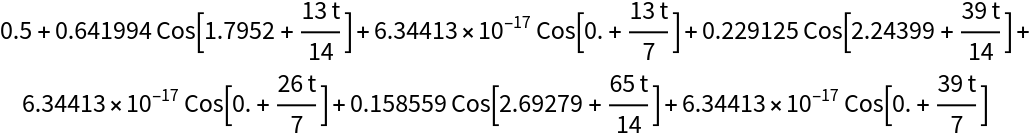 |
| In[18]:= |
| Out[18]= | 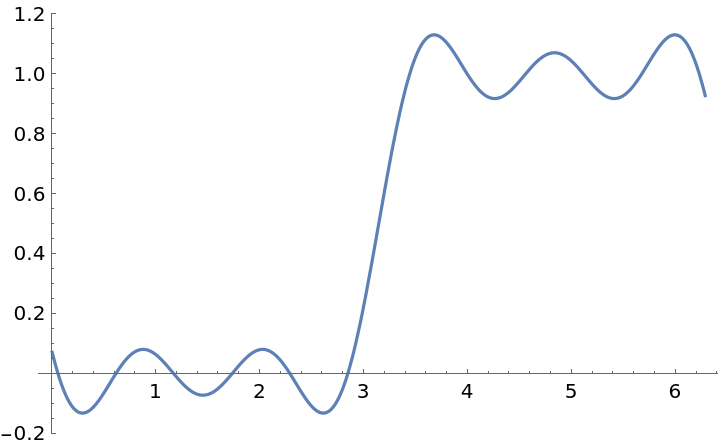 |
Instead of specifying the number of terms to return, you can specify a criteria for deciding when a Fourier term is significant enough to use:
| In[19]:= |
| Out[19]= |
When a fixed number of terms is requested, you can specify which terms are more important with "TermOrderingFunction". Here terms with the largest real component are used first:
| In[20]:= |
| Out[20]= |
Create a smooth parametric outline from an image:
| In[21]:= | ![pts = Position[ImageData[EdgeDetect[ImageRotate[\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztXQnIV8UWLzX7KhKxbF94UJil7YUtVEIFVpAptoqtPjPre6WGCEX1KGgP
KiqIEKPNbKVSiopELCkyKqJs+UzDFlvIKMu2+zzz3u/P/OfNmTkzd+72//4H
5vvu/87MmTNnfnPOuffOnfuPC/414Z8DNttss1k9m/5MOH/O2Jkzz587ceim
H5N6Z02f1jv1onG9s6dOmzpzzAUDN5389//SoE3p77//zkB0jN84Ns/pZblz
Juk8fG2ZvDl5JHmSxMnKlcnDI4+cvj7E6kcybi5+trH36c7Gm8MBd04iY8h4
uYir58sPxZcUpyE8fPV8uulS/yRuftcVI3WVq2qS6EVi2yT+IwVeQuT1tcfJ
EOKbQH/99Vf2xx9/ZH/++WeQf/PJL/UtPn6+dqV6lcok5RWbH0IS/x3LA+OO
ZBLhwawvGac8ssaSDa952pf2x6cPVywjlclllzhZfP3HMWHApFWrVmV33nln
9sILL2QbNmxQ5wgfsXNDMjZcXZvcLnsQYr99PPoLAQMfffRRNnXq1GzGjBlZ
b29vtttuu2WbLqNVGjFihMIDkc1WNJVix1p6XZHX30hlk/o3TibCAJ377LPP
sh122KE17khbbLFFNmjQoNbxSy+9pOrBR/jakMYLrj5xtkHCwyWH1B7YbAv3
29auT06XDDYKkYerY7b9+++/q//XXXedGuuenp5s4MCBauw333zzFh7oHP0f
NmxYtnr1asUDdsTXf5uuXH0LSVIeXL5PxxLZuHp5+hUiR6ycesK8Hjt2rBp3
jLctwS6cc845qg5iBUk7MTrJMzYpUwzF1uN4+fjlaQ8YuPrqq9vmPJcIJ5SG
DBmSffnll6quLb7sUhzlxU5MfYzfunXrsq233ro1xi4c6GnFihVtfIqQsS7E
2TUcm2Vi7YuPv+2/TwZfPxDzL1y4UGQLYA/o/zbbbJOtXbtW1Uec6ZPD1Q+J
zkP8jrRciM/yySnhISnPtSGRI4YHcHDPPfcovw/f70rACsUSRMCAFOuuMhxu
bH0x69l4SOaDTw6JvFKsVZ1cslN88Ouvv2bXXnttWxzoswfbbbedus4kHqZf
kOLCHEPbOdcc8pUJ4SHly9WV9EtKIXWleNZ/2/QEm/Dss8+K40SU++STT1Rd
3Sb45HD1w8fDNZau+SjRA9c+R7Y2bHyl9icvhdg5W1k8P3r33XdFsSHZC8LA
AQccYI0LYmSWzuUYjPhsU6j95GSX5HP9CeUbWlbSF1w3Ll++vG2++9LcuXNV
PdiTWDl8YyHVR8pkw1WnE3z722+/7cQBrin32Wef7Oijj84+/PBDpafuvYPm
E40j3VOmsfzll1+ynXfemcUC4oann366rX5oe00ll+wp+yXhpdusGJ6wdVhj
oFNfX1+2//77KwwMGDDg/3CAc4sXL1bl6RqDk4fzw7H9KJpc8uf1L1IevnI+
XiFtUSygPyNcv359tmDBguzUU09V9xNdfoFwQImwsnLlylabtrVKnZp8+LHl
2/DP8ZHgwYchV/tE+vi/+eab2eWXX57tueee4nvIuk2gZ9OPPvpom00hG2Nb
q+SjkLJF8uh0gh0geuONN9TcN/0+Jel1gu4zRo8enV1zzTXZe++912qPW5PQ
adQ07GFtwd13390W+9N9AFscIElmDEG8jjvuuOydd95RbbnWKkntVyil4BHa
XlMIc/PBBx9szWXJM4QQP6HzGzp0aCuO5K4nm4oDLj5wxQ6x8Zwv38XLJGCA
7heT3acxC3mmHJqAh8GDB6t7k7oMLl1KyVW36PFvasL93jVr1rSuA2J9QAwW
6D4T4saqdZE3NZngn++///628Skjoa377rtPydCpcaMPI2VjyPQnRND9xIkT
vesNUyf4H7ompXuU3Lyy+UKub7Y6Ph76eQkPs7zJ12UvqrZZNlkQn/3444+t
NehFxgUum/DAAw8oWSTPomJ0LMkP4WErayPpXK/KJhBB54sWLSotLjAT7keM
GjWqbT1z6r7afkvzpGWaGicAB5dddlnpsYGJBfr/+OOPt8llUpnjkKctDn8+
n1YFhiAT6XzkyJGV2QPgj2zC+PHjlWz6O5E+nx3S37w8pHxDfI4pj6s+JztX
3/ebEuJDuq9X9P0CXwL+9tprr2zjxo1t+uX0aBuHEJ1wPKR6NutKY4y6JdxD
vummmyr1CZSAQZIBzyd99xOkOpeUk+RLy5RJedul+rhWOPLII9t8dFUJ7T/x
xBNKria9I10VDvISMPDxxx+rd5JD300qKkag//RMkqhJOABVbeNDEhF8wu23
3165TzDtwYQJE5Rsqe8z+8YpxTj68BGKKdtxCv4oD3tw7LHH1sInUEKsuO++
+0atUTH7yR37xiu2naYRMPDpp5+qvQuq9gdI3LuQTSQTH9L5Wiau4Hfnz59f
G59gYuH1119XMtp8g64z056blNeehthblx33+Q9bv4rGBHBwyy231A4HkOXh
hx9uyVp328uNYWxsUVaciBhx1qxZtcUB7blDRLLqc57TU9k65GSosv3QBHtw
7rnn1hYH3D46TUmmvTCxYrMptrq+fAlPbo4g9jrxxBOVzutwrYAEWWiNEpFt
v4TQOSmhIsbf1VYMcWMt5WmWAQ6OOuqo2uEA9mDSpElKRv1eUqz+UpNLjhQY
ijkn4WXmQ7dnnHFGbf0C7ikiPojpaxWpCpK2bZYDDubMmVNbHDz00ENtssb0
v8qxKZti+gnd0tpQvKNS9fgjYX3k+++/r2Rs0n0kqV1w+flUckh4454t1qLV
JT6AHGPGjFGy6xiwxYFmXyX6Dx0jzgdxx1wbJg8uPwUeJDjQ5fz++++zHXfc
sRbPGnWfcMcddyj5cJ/DlLuuONDPVR2juDCqJ/iGmTNnto1Blf6A0lZbbZV9
/vnnSrbQa8Y6pNSUF98chkG4b0/71cAnV2kT4BPGjRvXks/Xr1CKsQd1bCM1
Qdc333yzGgOsR6nCFlDbdPzyyy+3yWZS3XRoUojN5mxJzLm8/gP+4ZJLLikd
C7BD8EnHH3+8kqVT33PUdV8kSfyUmUe/Se/ki88777y2MSpq/LFnjn7utNNO
U+shSB7XtWLd7QFI4q9j66SKRVx8af+anXbaqZR17PRuNY3/smXLvLroUnmE
67SzzjpLjVPqawjEoieccEL26quvZn19fa22YZN08sW6Ztk8cTWXX9TcqwvZ
+oe9zOgZTxE4QCx4/fXXt9qksXftheKS19ef0DIpcOCLx1zlJPGGj495jvtt
8tLLIGY8/fTTk+MAeyRtueWWyg8Q3rhnSKG68pWX5ufhYdNn3nJVpSKfQ4LX
VVddpdpo6voSKSbLJGnbvnLIxzV7ar+AeJPuYf/000+sL5D0R5KfQiexbXF8
pRjJg6WQ/uh2ySTYg+nTpyfHAfkE2h8N1wYh+9/4MJySOH4h41iEfSnTpuF6
4a677kruF3Df+Mknn1RtdP1CfQlz9MUXX1RjlmovBPiF7bffXu2/Q9SkdQX9
jcx3X/UxTGELTjnllLZ2ulQNSeOIn3/+Odt1112T4QD+5YorrlD8pe8xu3y1
ND4LLSOVKzTGTBknpvQ/vngo5Z4IwMGtt96qePvWHPqOQ/sUQnl55I0tqopp
uFgx5Tsu4PHII48o3q41yN1UjwQcpHz3Eb7ltddeU7w79VqBks0uSGyFbosk
fGNskFnfVRY2e8mSJUmvGci/0NonIn19gaQfZp9dOnHZ6pQ8uDzXONnad50r
g7h2Ecv/8MMP2bBhw3LHiqi77bbbtr737tMJJy+n6xAMxfDwlZPyCJmveeUw
/7vKcCnlXin6d32/++47xde3/jRE1m4qJhEhRrjyyitzxwjAAa1toWcLnT6u
nUSIEejbi3ntAeKL3XffXX27j6jT9CUhV58l+ihTZ8A0/ALFdRjH2BgB9UeM
GNG295XeL24u4Zx0rvnKSPjEtmPKatoIl/2w6cIlK1eX48GVtf3Wk74XPz0r
znPdgHoHHXSQUx+2vvt0WIRNz1M2j6xV9dOHH5Q55JBDcuEAPuWII45Q/CTv
KJWpk9TtdhohRqA9LfO8Ew0c0Hf6iLrPmJpFwAHtV5XnmsF81tip318yKcbm
II8rY/K3lTPzzDL6b5+slGC/v/nmm2yXXXZhv+ftS8DP7NmzVZvSZwu+/pRp
62P8AneOw4ttfLgx4/J85V3nXDxgE+jdltjrR+CAvg0Knp3oRyVUp36HxDNU
Dlg4++yzo7CA68233npL8ekvfoEjl+5dY+OLRW12lOPr4sER/MNXX32lnhGE
3EtAOXpOQXtu+NoqikKwX1RbkhjAzCtDVpc8esL8XbFiRfAeCbAddO1JBEyZ
/XT5WDNf0i9XvssX29ri/L5Pb67+ueIISV+lc9uFLVdsYZMFfoHWGYf6BcQG
kydPVjxs+9yE6k+qX4luuPkYiwNfv6pIqWQCDp555pngawbgAO8z9qd1SBwO
pTh1lZe25WrPlu/iC79A+x2H3keAH3nsscdavELb71I9CPbghhtuCMYBYonl
y5crHnW6VigKb0XbdP2cLz+Ery/Bp4d+Cx5xxGGHHabWwZvvNLrkC9Fpat2n
asccL7NvLgy58jkcSLHoaos7RwR7MGPGjCAcmPvj6jGiq/8+vbnyuTxOB65+
+/hz/ehEQr9o/QitI6FxlcaJ+veaiU+dfEKRxM1pG75851K06+PtOof/sON9
fX1q/4qQe0iwB5deeqniYX7H3WejpGWk+WYZbq6H2EqpbbX1xdYWdy4vSXyN
7ZyJA9rHbPDgwVE4oD3dieqIA8nYSPwvl+fqi60t7pyEQsfalcfhYM2aNWpv
sxAcwC889dRTikeVOLCNWx4cmDxdbXVCAg7ovYOQZwsoQ3slf/HFF4pHE/dK
jkmdSOjXt99+q/YykeIAseShhx7a0fqJpTz6SF1XMj7Ip/WqtIeFFAeIDXp7
e1X9unyvuwxM6v5FbyvEnoTan7zlfTzgFzZs2JDtscce4utGxAYLFy5U9fXn
Ci69hPYptk4Mr9CxbCJx8uMcjePee+8twoEeG6xevVrVD1mbWic9xspSpz5I
iLNhZv769evV+4kSvwCcHHzwwc45Ure5U4Usdeq/i3APkL65LV2DYrt/FEup
9VQU9jrdbsQ8W0BssGDBgjYeRKHj0EQcpIpV6pTwbGjKlCkiHMBe0L3HVatW
qbpN+qZG6nGUYMOHJRuGQ9q0lZeeQ8I9wDPPPFOEA9iCAw880HrfKLQPTcRB
JxLiA3q3TYID5F944YWqXl3uG5RJJp708ykwavKOmWsh7eJab926deK9FIED
+tYTUeh6xBh9pdCxhFdIO03DgXlOlxlz+fnnn2+z+RIcXHzxxW04MOcKJ6ur
DFdPqmOdQnVk1vP1oZMIPmHx4sXBOKD92on6o1+oA6XEI/wCfVu1p6cnyC/A
HpSJA8l8LGPOcm247GIRMoSWt8mE/8CCdI9d4GD8+PGqnmuduimD61we/8f1
N5W/DvFFnJ5TUyxfTnb4Bul1I/KnTZum6tnsQci85coVjQNfWyHyND3BFtD7
qcOHDxf5BdgLWqNMPPrT+0scRjgcpyYJT70MjnW5bTwwl+fPny+OE/GM6ZVX
XlF1XWvVq6CQserSfwk+4eSTT259h1mCAyq73377qX1UiPrrNUOsLanantlk
ojHk1h1wPgLlDj/88NY+uhs3bqy8P3XwDaG2u0iyyWqe09enDhkyhB13shG2
dSmwHWQXPvjggxZPlx/qUv0IOFi5cqV1P1U6h/cZ8NtcnwAsEI5uu+224Fiq
qWTrJ9fvUF34bI2PX+g8RGxA++oCA0jAxdKlS7N58+apfVJNv0DXj4QD+tYX
sEHvtxEhXvDpyaVLSXlOD1wZF059dcz6Uh51nxOw4V9//XXrGww0pni3jb7X
rpd97rnnspNOOqmVb0u0fwJRf8FBWXFIijKuurAJ9C0drE2kNHLkyGzt2rVq
/Cn+04m+90eYuPHGG9VeOMccc4yKMylOWLRokeItXZcilT/lGFQ1nnVPiBNo
3GkP/nvvvVetWSXS15nQHOfeZ/7tt99a9xFSy2eby1Xz61TivsfNlSU8ABd6
3f6yr7KJJ/3Y1JtNjxIspcJbKHZpDGlsKfnG09bXWLl99YqYfy6e0vby2JK8
ZfK0303pUpOp6fLHUFF91vmmwIZZ3/aba9PVdhH95/rra0sii68veecjV5fT
r1Qek4fJy3bMtc2VtckUo1NfX0PybXnmeW7MJDrn2grBgWu8ub652rGd/w8F
ZSTa
"], {{0, 130.}, {130., 0}}, {0, 255},
ColorFunction->RGBColor,
ImageResolution->72],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{130., 130.},
PlotRange->{{0, 130.}, {0, 130.}}]\), -\[Pi]/2]]], 1];
man = ResourceFunction["TrigApproximateList"][
pts[[FindCurvePath[pts][[1]]]], t, 15, DataRange -> {0, 2 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/4f6/4f6b85c9-469e-48a2-a2fc-8190564ab5f9/236a6326235a2fc1.png) |
| Out[22]= |  |
| In[23]:= |
| Out[23]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License