Basic Examples (2)
Find the incenter where the dihedral angle bisectors intersect:
The incenter is the center of Insphere, tangent to the faces. Show it:
Scope (4)
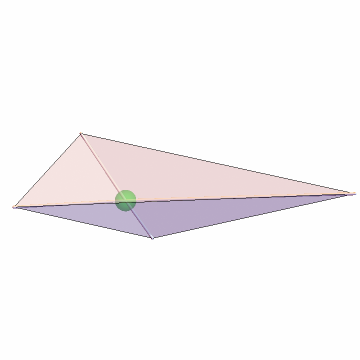
Find the centroid, which is the center of mass or the concurrence of the face centroids:
The centroid can also be found with Mean. Show it:
Find the circumcenter, where the edge-bisecting perpendicular planes intersect:
The circumcenter is the center of the Circumsphere. Show it:
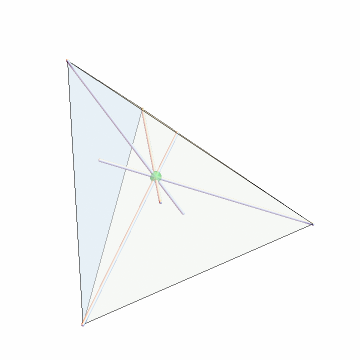
In a tetrahedron, a midplane is perpendicular to one edge and concurrent with the midpoint of the opposing edge. Find the Monge point, the concurrence of the midplanes:
Calculate the cevians of the Monge point:
Show the Monge point and the cevians:
Here are the available SubTetrahedron items:
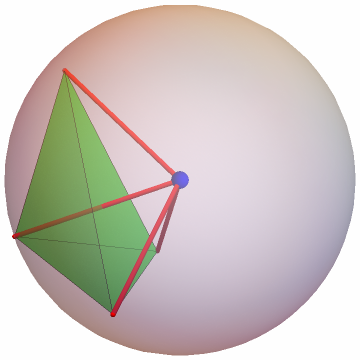
For example, here's the reflection tetrahedron, resulting from reflecting each vertex by the opposite face:
Connecting the vertices shows a perspector point where the tubes intersect, namely the Monge point:
Possible Issues (1)
Various triangle center points, such as the orthocenter, don't always have a tetrahedron center.
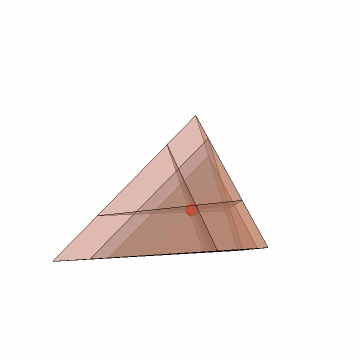
For example, in 2D, the Gergonne point is the perspector of the contact triangle, but the lines do not coincide in 3D given the contact tetrahedron:
Neat Examples (5)
The symmedian point has the minimal total distance squared to the faces:
Check that:
Show the symmedian point:
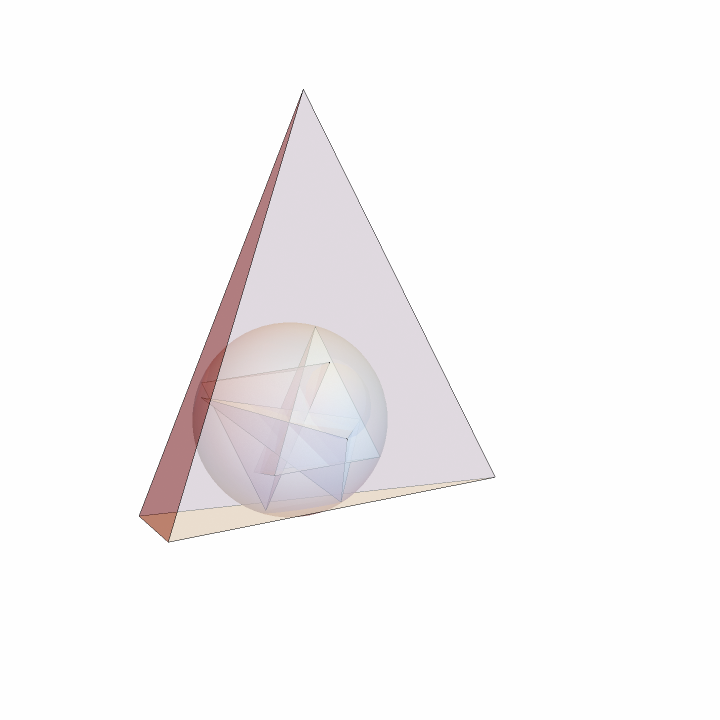
Find the Euler, Euler projected and medial tetrahedra:
The spheres are all identical. This unique sphere is also known as the 12-point sphere:
Show the 12-point sphere:
The Fermat point minimizes the total distance to the vertices:
Check that:
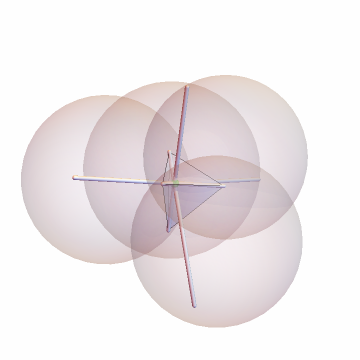
Let S be the sum of distances to the Fermat point. The Fermat tetrahedron is a set of segment endpoints S away from the vertices and passing through the Fermat point:
Circumspheres of the Fermat point and three vertices coincide with the segment endpoints:
Calculate the Euler-medial tetrahedron and find the Euler-medial point:
Show that the point is the perspector of the original and Euler-medial tetrahedron:
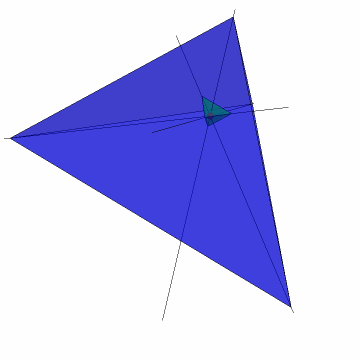
Find the parallelians point:
Move the tetrahedron and calculate the area of the parallel triangles through the point:
Show the parallelians point and the equal area parallel triangles:
![Graphics3D[{{Opacity[.5], tet, Green, Sphere[ii, 33/14]}, Tube[{ii, #}] & /@ PolyhedronCoordinates[tet]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/4890a656ffa775be.png)
![tet = {{-22, -25, 4}, {-12, 15, -6}, {8, 5, -6}, {18, -15, 24}};
facecentroids = Reverse[Mean /@ Subsets[tet, {3}]];
gg = ResourceFunction["TetrahedronCenter"][tet, "Centroid"]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/06aa1b953197d357.png)
![Graphics3D[{{Opacity[.5], Tetrahedron[tet], Green, Sphere[gg, 1]}, Tube /@ Transpose[{tet, facecentroids}]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/0a82820ae9245904.png)
![Graphics3D[{{Opacity[.5], Sphere[oo, Sqrt[689]/4], Green, Tetrahedron[tet]}, Blue, Sphere[oo, 1/3], Red, Tube[{oo, #}] & /@ tet}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/71104a0fdd1b6518.png)
![Graphics3D[{{Opacity[.5], Tetrahedron[tet]}, Red, Sphere[mm, .1], Green, Tube /@ Transpose[{tet, mongecevians}]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/278af628d53b8ba8.png)
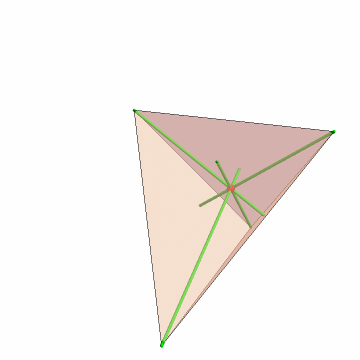

![Graphics3D[{{Opacity[.5], Tetrahedron[tet], Tetrahedron[ref], Red, Sphere[ResourceFunction["TetrahedronCenter"][tet, "Monge"], .2]}, Blue, Tube[#] & /@ Transpose[{tet, ref}]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/5f03826fdcc728e3.png)

![tet = {{0, 0, 0}, {1, 2, 1}, {3, 0, 0}, {1, 1, 4}};
con = RootReduce[ResourceFunction["SubTetrahedron"][tet, "Contact"]];
Graphics3D[{{Opacity[.5], Red, Tetrahedron[tet], Green, Tetrahedron[con]}, Blue, Tube[#] & /@ Transpose[{tet, con}], Opacity[.2], Insphere[tet]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/6b85c869615d2f8a.png)

![planes = ResourceFunction["HessianPlane"][#] & /@ Subsets[tet, {3}];
RootApproximant[{x, y, z} /. Last[NMinimize[
Quiet@Total[({x, y, z, 1} . #)^2 & /@ planes], {x, y, z}, WorkingPrecision -> 60, Method -> "SimulatedAnnealing"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/45e11d46f3b444bd.png)

![initial = {{0, 0, 0}, {1, 3, 0}, {3, 0, 0}, {1, 1, 2}};
tetras = ResourceFunction["SubTetrahedron"][initial, #] & /@ {"Euler", "EulerProjected", "Medial"};
spheres = Circumsphere /@ tetras](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/61bdf086973dde36.png)
![Graphics3D[{Opacity[.5], Thick, Tetrahedron[initial], spheres[[1]], Tetrahedron /@ tetras}, Boxed -> False, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/30ba6d66bec2e745.png)
![{x, y, z} /. Last[NMinimize[
Quiet@
Total[ResourceFunction["RealEuclideanDistance"][{x, y, z}, #] & /@
tet], {x, y, z}, WorkingPrecision -> 60, Method -> "SimulatedAnnealing"]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/5ae453be734c5654.png)

![Graphics3D[{{Opacity[.5], Tetrahedron[tet], Green, Sphere[xx, 3]}, Tube /@ Transpose[{tet, fermatTetra}], Opacity[.2], Circumsphere /@ Take[Subsets[Prepend[tet, xx], {4}], 4]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/33998ed6a499abd7.png)
![tet = {{2, 2, 2}, {0, 0, 6}, {0, 8, 6}, {6, 2, 9}}; eulermedial = ResourceFunction["SubTetrahedron"][
ResourceFunction["SubTetrahedron"][tet, "Euler"], "Medial"];
em = RootReduce[
ResourceFunction["TetrahedronCenter"][tet, "EulerMedial"]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/036305ee90952f90.png)
![Graphics3D[{{Opacity[.5], Blue, Tetrahedron[tet], Green, Tetrahedron[eulermedial]}, InfiniteLine /@ Transpose[{tet, eulermedial}], Red, Sphere[em, .1]}, Boxed -> False, ImageSize -> Small, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/2e1fb172dba7528a.png)
![tet = {{0, 0, 0}, {1, 3, 0}, {3, 0, 0}, {1, 1, 2}};
para = N[ResourceFunction["TetrahedronCenter"][tet, "Parallelians"]]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/491ecbe9860fc821.png)
![new = # - para & /@ tet;
planes = Take[#, 3] & /@ (N[ResourceFunction["HessianPlane"][#]] & /@ Reverse[Subsets[new, {3}]]);
triangles = Table[RegionIntersection[Hyperplane[planes[[k]], {0, 0, 0}], Tetrahedron[N[new]]], {k, 1, 4}];
Area /@ triangles](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/1feb849052baaf26.png)
![Graphics3D[{{Opacity[.5], Tetrahedron[new], Gray, triangles}, Red, Sphere[{0, 0, 0}, .1]}, Boxed -> False, ImageSize -> Small, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/41f/41f2840a-25fa-4180-b028-e9660c2ad419/662f82772ea3849f.png)