Function Repository Resource:

TaylorPolynomial

Source Notebook

Compute the Taylor polynomial of a given order of a function of one or several variables

Contributed by: Dennis M Schneider

ResourceFunction["TaylorPolynomial"][f,{x,x₀,n}]

computes the Taylor polynomial of the function f of a single variable about the point x₀ of degree n.

ResourceFunction["TaylorPolynomial"][f,{x,y,…},{x₀,y₀,…},n]

computes the Taylor polynomial of the function f of several variables about the point (x₀,y₀,…) of degree n.

Details and Options

With some functions it is necessary to use limits to compute the terms of the series. For these functions, set the option "UseLimit" to True.

Examples

Basic Examples (4)

A simple example:

In[1]:=

Out[1]=

It returns the same result as:

In[2]:=

Out[2]=

An example of a Taylor polynomial of a function of three variables:

In[3]:=

$tp = ResourceFunction["TaylorPolynomial"][ Exp[x y^2] Log[1 + z^2], {x, 0}, {y, 0}, {z, 0}, 7]$

Out[3]=

Compare with Mathematica's Series command. The two commands treat the expansion differently; TaylorPolynomial expands to a total degree of each term, while Series expands in each variable separately:

In[4]:=

$mseries = Normal[Series[ Exp[x y^2] Log[1 + z^2], {x, 0, 7}, {y, 0, 7}, {z, 0, 7}]]$

Out[4]=

Here is the difference between the two commands:

In[5]:=

Out[5]=

The Taylor polynomial of a function of two variables:

In[6]:=

$tp = ResourceFunction["TaylorPolynomial"][ Exp[x^2] Log[1 + y], {x, y}, {0, 0}, 5]$

Out[6]=

Plot the function together with its fifth degree Taylor polynomial:

In[7]:=

$Plot3D[{Exp[x^2] Log[1 + y], tp}, {x, -1, 1}, {y, -1, 1}]$

Out[7]=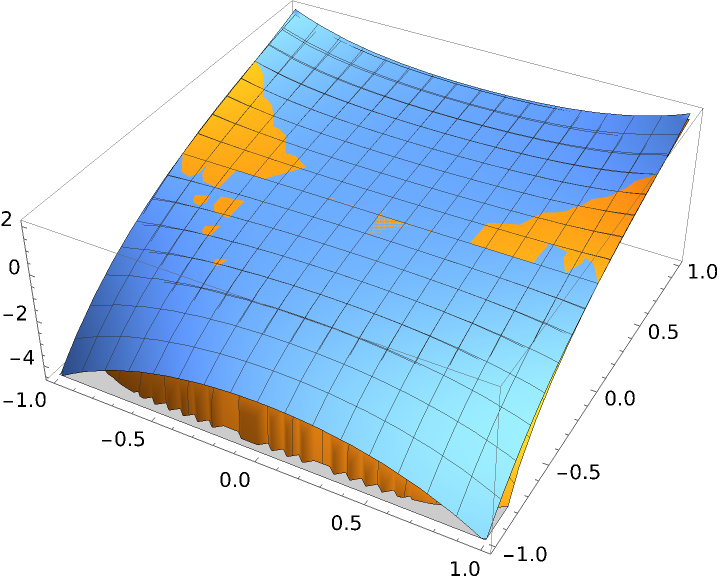

The Taylor polynomial of a function with a removable singularity at the origin:

In[8]:=

$Clear[f] f[x_, y_] := Sin[x y^2]/(x y^2) ResourceFunction["TaylorPolynomial"][f[x, y], {x, y}, {0, 0}, 18]$

Out[10]=

This can be obtained by making a simple substitution in a univariate function:

In[11]:=

$ResourceFunction["TaylorPolynomial"][Sin[x]/x, {x, 0, 6}] /. x -> x y^2$

Out[11]=

Scope (3)

The Taylor polynomial of degree 2 for a symbolic function centered at (a,b):

In[12]:=

Out[13]=

An infinitely differentiable function of one variable that is not the zero function but all of whose Taylor polynomials are 0:

In[14]:=

$Clear[f] f[x_] := \[Piecewise] { {Exp[-(1/x^2)], x > 0}, {0, x <= 0} } ResourceFunction["TaylorPolynomial"][f[x], {x, 0, #}, "UseLimit" -> True] & /@ Range[8]$

Out[16]=

Without using limits:

In[17]:=

$Clear[f] f[x_] := \[Piecewise] { {Exp[-(1/x^2)], x > 0}, {0, x <= 0} } ResourceFunction["TaylorPolynomial"][f[x], {x, 0, #}] & /@ Range[8] // Simplify$

Out[19]=

An infinitely differentiable function of two variables that is not the zero function but all of whose Taylor polynomials are 0:

In[20]:=

$Clear[f] f[x_, y_] := \[Piecewise] { {x Exp[-1/(x^2 + y^2)], {x, y} != {0, 0}}, {0, True} } ResourceFunction["TaylorPolynomial"][f[x, y], {x, y}, {0, 0}, #, "UseLimit" -> True] & /@ Range[8]$

Out[22]=

Without using limits:

In[23]:=

$f[x_, y_] := \[Piecewise] { {x Exp[-1/(x^2 + y^2)], {x, y} != {0, 0}}, {0, True} } ResourceFunction["TaylorPolynomial"][f[x, y], {x, y}, {0, 0}, #] & /@ Range[8]$