Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SzegedIndex

Source Notebook

Compute the Szeged index of an undirected graph or a molecule

Contributed by: Jan Mangaldan

ResourceFunction["SzegedIndex"][g]

computes the Szeged index of the graph g.

ResourceFunction["SzegedIndex"][mol]

computes the Szeged index of the molecule mol.

Details

The Szeged index is also known as the edge-Szeged index.
The Szeged index generalizes the Wiener index to undirected graphs with cycles.
For an undirected connected graph, the Szeged index is defined as , where νi counts the number of vertices that are nearer to the ith vertex than to the jth vertex and the sum ranges over all edges of the graph.
ResourceFunction["SzegedIndex"][mol] computes the Szeged index of a molecule mol, where the hydrogens are ignored by default. Use the option setting IncludeHydrogens→All to account for hydrogens.
ResourceFunction["SzegedIndex"][entity] computes the Szeged index of an entity of type "Chemical" or "Graph".

Examples

Basic Examples (1) 

The Szeged index of a Petersen graph:

In[1]:=
ResourceFunction["SzegedIndex"][PetersenGraph[]]
Out[1]=

Scope (2) 

Compute the Szeged index of a molecule:

In[2]:=
ResourceFunction["SzegedIndex"][ Molecule[{"C", "C", "C", "C", "C", "C", "C", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, { Bond[{1, 2}, "Single"], Bond[{2, 3}, "Single"], Bond[{3, 4}, "Single"], Bond[{4, 5}, "Single"], Bond[{5, 6}, "Single"], Bond[{6, 7}, "Single"], Bond[{6, 1}, "Single"], Bond[{7, 3}, "Single"], Bond[{1, 8}, "Single"], Bond[{1, 9}, "Single"], Bond[{2, 10}, "Single"], Bond[{2, 11}, "Single"], Bond[{3, 12}, "Single"], Bond[{4, 13}, "Single"], Bond[{4, 14}, "Single"], Bond[{5, 15}, "Single"], Bond[{5, 16}, "Single"], Bond[{6, 17}, "Single"], Bond[{7, 18}, "Single"], Bond[{7, 19}, "Single"]}, {}]]
Out[2]=

Compute the Szeged index of a named entity:

In[3]:=
ResourceFunction["SzegedIndex"][Entity["Graph", "TutteGraph"]]
Out[3]=

Options (2) 

IncludeHydrogens (2) 

By default, hydrogens are ignored in the computation of the Szeged index:

In[4]:=
ResourceFunction["SzegedIndex"][Molecule["neopentane"]]
Out[4]=

Use IncludeHydrogens→All to account for hydrogens:

In[5]:=
ResourceFunction["SzegedIndex"][Molecule["neopentane"], IncludeHydrogens -> All]
Out[5]=

Applications (2) 

Generate all alkanes with 7 carbon atoms (heptanes) using the resource function AlkaneIsomers:

In[6]:=
heptanes = ResourceFunction["AlkaneIsomers"][7]
Out[6]=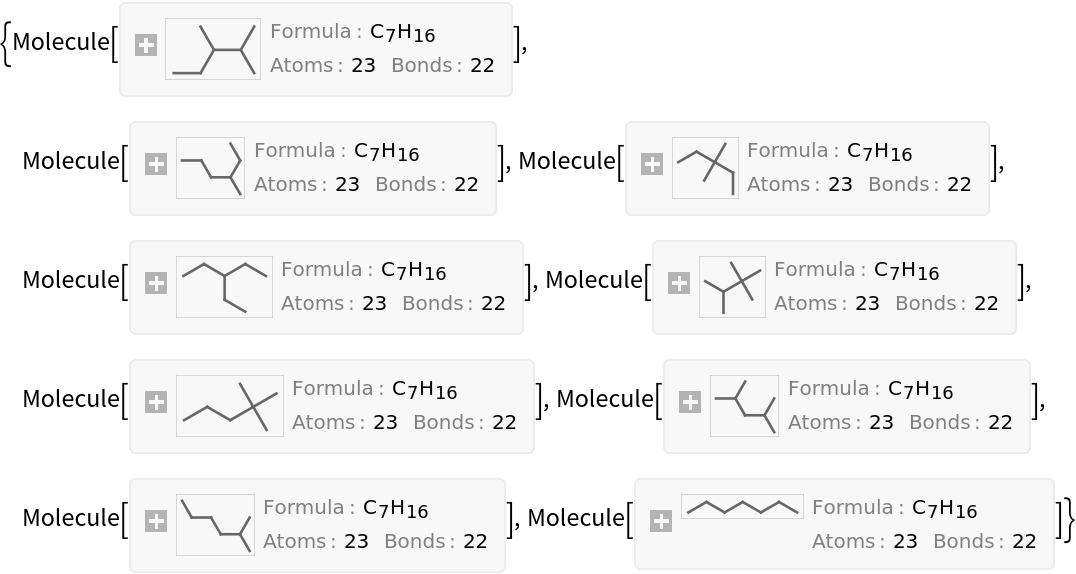

Sort the heptane isomers by their Szeged index. This effectively sorts them from "most branched" to "least branched":

In[7]:=
SortBy[heptanes, ResourceFunction["SzegedIndex"]]
Out[7]=

Properties and Relations (2) 

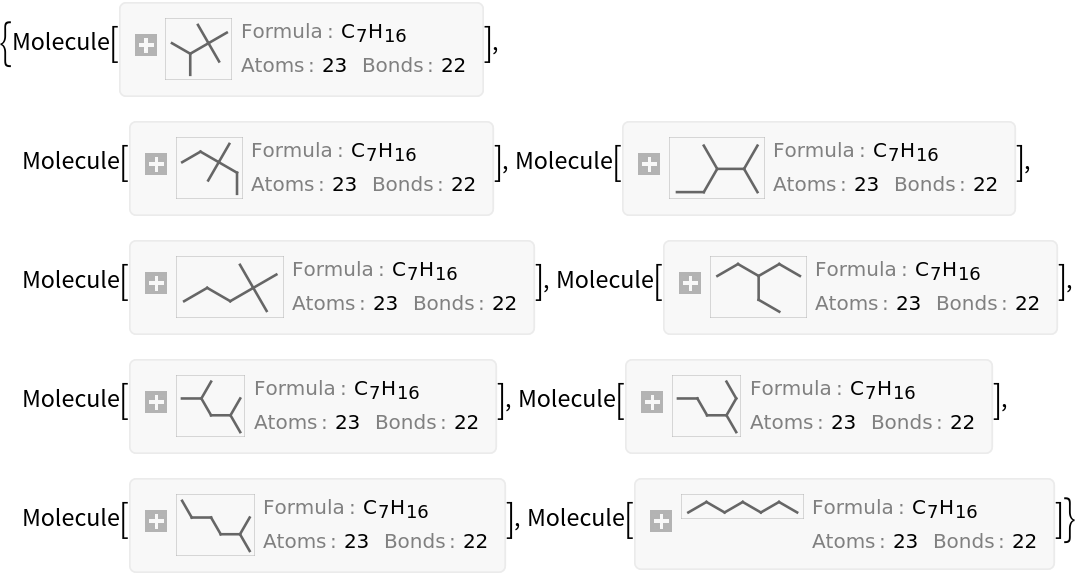Define a function for computing the Wiener index of a graph:

In[8]:=
WienerIndex[g_?GraphQ] := Total[GraphDistanceMatrix[g], 2]/2

For an acyclic graph, the Szeged index is equivalent to the Wiener index:

In[9]:=
g = \!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null, {{3, 4}, {5, 6}, {5, 3}, {7, 8}, {7, 1}, {7, 2}, {7, 3}, {9, 10}, {9, 2}}}]]}, TagBox[GraphicsGroupBox[ GraphicsComplexBox[{{0., 1.466033332275663}, { 0.7330166661378313, 1.466033332275663}, { 1.8325416653445783`, 1.466033332275663}, { 1.4660333322756627`, 0.7330166661378315}, { 2.199049998413494, 0.7330166661378315}, {2.199049998413494, 0.}, {1.2827791657412049`, 2.199049998413494}, { 2.5655583314824097`, 1.466033332275663}, { 0.7330166661378313, 0.7330166661378315}, { 0.7330166661378313, 0.}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1, 7}, {2, 7}, {2, 9}, {3, 4}, {3, 5}, {3, 7}, {5, 6}, {7, 8}, {9, 10}}, 0.027040802458717428`]}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.027040802458717428], DiskBox[2, 0.027040802458717428], DiskBox[3, 0.027040802458717428], DiskBox[4, 0.027040802458717428], DiskBox[5, 0.027040802458717428], DiskBox[6, 0.027040802458717428], DiskBox[7, 0.027040802458717428], DiskBox[8, 0.027040802458717428], DiskBox[9, 0.027040802458717428], DiskBox[10, 0.027040802458717428]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->"NetworkGraphics", FormatType->TraditionalForm, FrameTicks->None]\); {WienerIndex[g], ResourceFunction["SzegedIndex"][g]}
Out[10]=

The Szeged index is equal to half the sum of all elements of the Szeged matrix:

In[11]:=
g = \!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null, {{3, 4}, {5, 6}, {5, 3}, {7, 8}, {7, 1}, {7, 2}, {7, 3}, {9, 10}, {9, 2}}}]]}, TagBox[GraphicsGroupBox[ GraphicsComplexBox[{{0., 1.466033332275663}, { 0.7330166661378313, 1.466033332275663}, { 1.8325416653445783`, 1.466033332275663}, { 1.4660333322756627`, 0.7330166661378315}, { 2.199049998413494, 0.7330166661378315}, {2.199049998413494, 0.}, {1.2827791657412049`, 2.199049998413494}, { 2.5655583314824097`, 1.466033332275663}, { 0.7330166661378313, 0.7330166661378315}, { 0.7330166661378313, 0.}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1, 7}, {2, 7}, {2, 9}, {3, 4}, {3, 5}, {3, 7}, {5, 6}, {7, 8}, {9, 10}}, 0.027040802458717428`]}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.027040802458717428], DiskBox[2, 0.027040802458717428], DiskBox[3, 0.027040802458717428], DiskBox[4, 0.027040802458717428], DiskBox[5, 0.027040802458717428], DiskBox[6, 0.027040802458717428], DiskBox[7, 0.027040802458717428], DiskBox[8, 0.027040802458717428], DiskBox[9, 0.027040802458717428], DiskBox[10, 0.027040802458717428]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->"NetworkGraphics", FormatType->TraditionalForm, FrameTicks->None]\); ResourceFunction["SzegedIndex"][g] == Total[ResourceFunction["SzegedMatrix"][g], 2]/2
Out[12]=

Requirements

Wolfram Language 12.3 (May 2021) or above

Version History

  • 1.0.0 – 20 December 2023

Source Metadata

  • Citation:
    • Gutman I., "A formula for the Wiener number of trees and its extension to graphs containing cycles." Graph Theory Notes of New York, vol. 27, no. 2, 9–15, 1994.
    • Gutman I., Dobrynin A.A., "The Szeged index - A success story." Graph Theory Notes of New York, vol. 34, no. 1, 37–44, 1998.
    • Klavžar S., Rajapakse A., Gutman I., "The Szeged and the Wiener index of graphs." Applied Mathematics Letters, vol. 9, no. 5, 45–49, 1996.
      DOI: 10.1016/0893-9659(96)00071-7

Related Resources

License Information