Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SymmetricSort

Source Notebook

Symmetrically reorder the rows and columns of a square matrix

Contributed by: Edmund B Robinson

ResourceFunction["SymmetricSort"][matrix,from,to]

symmetrically reorders the elements of matrix from ordering from to ordering to.

ResourceFunction["SymmetricSort"][matrix,index]

symmetrically reorders the elements of matrix by the ordering represented by index.

Details

ResourceFunction["SymmetricSort"] maintains matrix symmetry when permuting the matrix elements.
ResourceFunction["SymmetricSort"] takes any expression that satisfies SquareMatrixQ for matrix.
In ResourceFunction["SymmetricSort"][matrix,from,to], from and to can be any expression that satisfies VectorQ and DuplicateFreeQ, and together satisfy ContainsOnly. matrix, from and to must all have the same length.
In ResourceFunction["SymmetricSort"][matrix,index], index can be any ordering represented as a permutation list or as a disjoint cycle.

Examples

Basic Examples (5) 

Generate a covariance matrix from example data:

In[1]:=
obs = ExampleData[{"Statistics", "BlackCherryTrees"}, "DataElements"]; colNames = ExampleData[{"Statistics", "BlackCherryTrees"}, "ColumnHeadings"]; treeCov = Covariance@obs; TableForm[treeCov, TableHeadings -> {colNames, colNames}]
Out[1]=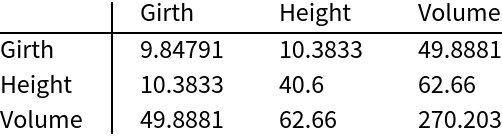

The covariance matrix is symmetric and positive semidefinite:

In[2]:=
Through@{SymmetricMatrixQ, PositiveSemidefiniteMatrixQ}@treeCov
Out[2]=

A SymmetricSort using the variable names to change the order of the variables:

In[3]:=
newOrdering = {"Volume", "Girth", "Height"}; sstreeCov = ResourceFunction["SymmetricSort"][treeCov, colNames, newOrdering]; TableForm[sstreeCov, TableHeadings -> {newOrdering, newOrdering}]
Out[3]=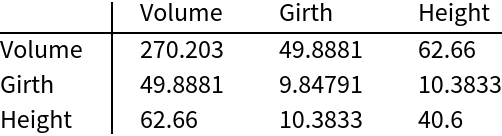

Symmetric and positive semidefinite properties are preserved:

In[4]:=
Through@{SymmetricMatrixQ, PositiveSemidefiniteMatrixQ}@sstreeCov
Out[4]=

SymmetricSort can also take an ordering of position indices:

In[5]:=
ordering = {3, 1, 2}; isstreeCov = ResourceFunction["SymmetricSort"][sstreeCov, ordering]; TableForm[isstreeCov, TableHeadings -> {newOrdering[[ordering]], newOrdering[[ordering]]}]
Out[5]=

Scope (2) 

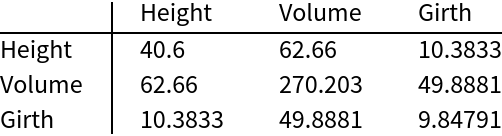SymmetricSort preserves the diagonal and the relative positions of the upper and lower off-diagonals:

In[6]:=
MatrixForm[m = Table[Indexed[\[FormalM], {r, c}], {r, 4}, {c, 4}]]
Out[6]=

Diagonal elements in the original matrix remain on the diagonal in the reordered matrix, and off-diagonal relative positions are comparable. For example, m34 is still mirrored with m43:

In[7]:=
ResourceFunction["SymmetricSort"][m, {3, 1, 4, 2}] // MatrixForm
Out[7]=

SymmetricSort accepts permutations expressed in cycle format:

In[8]:=
ResourceFunction["SymmetricSort"][HilbertMatrix[6], Cycles[{{1, 5, 4}, {2, 3}}]] // MatrixForm
Out[8]=

Applications (2) 

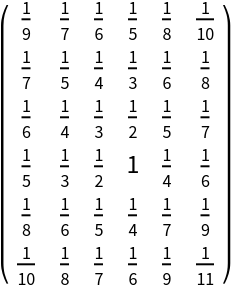Properties of Graph, like WeightedAdjacencyMatrix, are given in the order of VertexList:

In[9]:=
g = Graph[{2 \[DirectedEdge] 3, 3 \[DirectedEdge] 1, 1 \[DirectedEdge] 2, 3 \[DirectedEdge] 2}, EdgeWeight -> {12, 18, 3, 7}]; vl = VertexList[g]; wam = WeightedAdjacencyMatrix[g]; TableForm[wam, TableHeadings -> {vl, vl}]
Out[9]=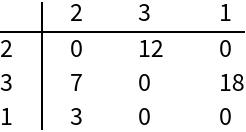

SymmetricSort property elements in canonical order:

In[10]:=
ns = NumericalSort@vl; sswam = ResourceFunction["SymmetricSort"][wam, vl, ns]; TableForm[sswam, TableHeadings -> {ns, ns}]
Out[10]=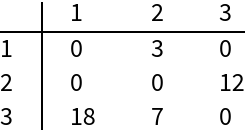

SymmetricSort the HadamardMatrix:

In[11]:=
MatrixForm[ sshm = ResourceFunction["SymmetricSort"][ HadamardMatrix[4], {3, 2, 4, 1}]]
Out[11]=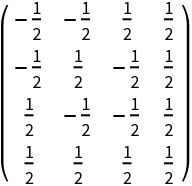

The permuted matrix is involutory, just like the original Hadamard matrix:

In[12]:=
sshm . sshm == IdentityMatrix[4]
Out[12]=

Properties and Relations (1) 

The eigenvalues of a symmetric matrix are invariant under SymmetricSort:

In[13]:=
MatrixForm[ sym = Symmetrize[RandomReal[{-1, 1}, {5, 5}], Symmetric[{1, 2}]]]
Out[13]=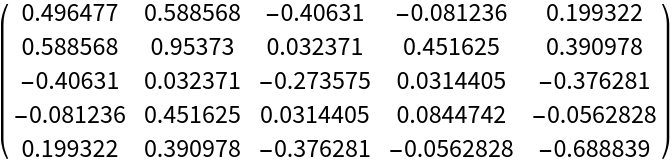
In[14]:=
Eigenvalues[sym]
Out[14]=
In[15]:=
Eigenvalues[ ResourceFunction["SymmetricSort"][sym, RandomPermutation[5]]]
Out[15]=

Neat Examples (5) 

An upper bidiagonal matrix:

In[16]:=
MatrixForm[ bi = Normal[ SparseArray[{Band[{1, 1}] -> Array[\[FormalD], 5], Band[{1, 2}] -> Array[\[FormalE], 4]}]]]
Out[16]=

Generate a symmetric block matrix with bidiagonal blocks:

In[17]:=
MatrixForm[biblk = ArrayFlatten[{{0, Transpose[bi]}, {bi, 0}}]]
Out[17]=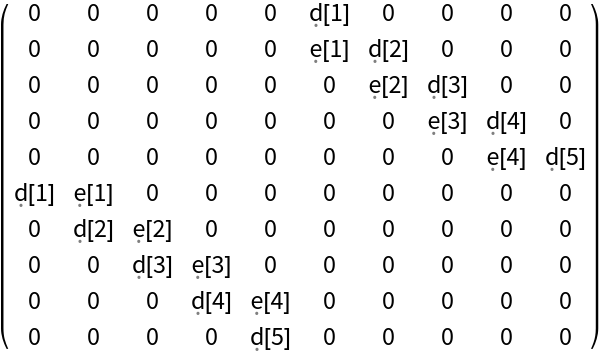

Use the resource function OutShuffle with SymmetricSort to transform the matrix into a tridiagonal matrix:

In[18]:=
ResourceFunction["SymmetricSort"][biblk, ResourceFunction["OutShuffle"][Range@Length[biblk]]] // MatrixForm
Out[18]=

Compute the singular values of a numerical upper bidiagonal matrix:

In[19]:=
SingularValueList[ bi2 = Normal[ SparseArray[{Band[{1, 1}] -> {1., 3., 5., 7., 9., 11., 13.}, Band[{1, 2}] -> {2., 4., 6., 8., 10., 12.}}]]]
Out[19]=

These are equivalent to the positive eigenvalues of the permuted block matrix:

In[20]:=
Select[Eigenvalues[ ResourceFunction["SymmetricSort"][ ArrayFlatten[{{0, Transpose[bi2]}, {bi2, 0}}], ResourceFunction["OutShuffle"][Range[2 Length[bi2]]]]], Positive]
Out[20]=

Publisher

Edmund B Robinson

Version History

  • 1.0.0 – 01 September 2021

License Information