Function Repository Resource:

OutShuffle

Source Notebook

Perform an out shuffle on a list

Contributed by: Sander Huisman

ResourceFunction["OutShuffle"][list]

performs an out shuffle on list.

ResourceFunction["OutShuffle"][list,n]

performs n out shuffles on list.

Details and Options

An out shuffle is defined as follows: (1) split the list in two halves; and (2) interweave each half of the list starting with the first half, such that every other card comes from the same half of the list.

Here is an example of a list with 10 items:

When the list has an odd length n, the first "half" will be (n+1)/2 long and the second "half" will be (n-1)/2 long:

Examples

Basic Examples (1)

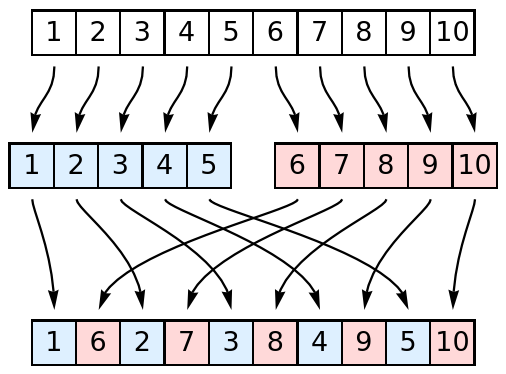
Perform an out shuffle on a list of 10 items:

In[1]:=

Out[1]=

Scope (2)

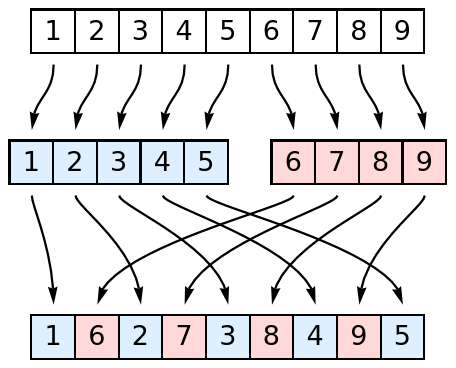
Perform an out shuffle 3 times to a list:

In[2]:=

Out[2]=

Confirm that this is the same:

In[3]:=

Out[3]=

The list can contain expressions of different types:

In[4]:=

Out[4]=

Applications (3)

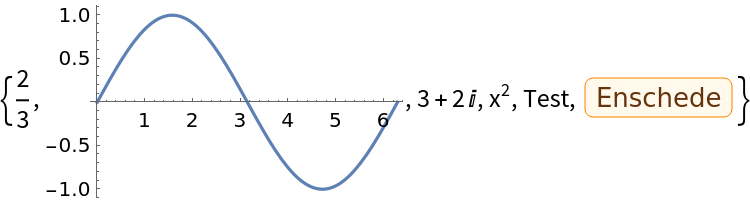Create a sorted deck of cards:

In[5]:=

$deck = StringJoin@*Reverse /@ Tuples[{{"\[SpadeSuit]", "\[HeartSuit]", "\[DiamondSuit]", "\[ClubSuit]"}, Join[{"A"}, ToString /@ Range[2, 10], {"J", "Q", "K"}]}]$

Out[5]=

Shuffle the deck once:

In[6]:=

Out[6]=

The original is obtained after only 8 out shuffles:

In[7]:=

Out[7]=

Properties and Relations (3)

An out shuffle does not change the first and last items for a list of even length:

In[8]:=

Out[8]=

An out shuffle does not change the first element:

In[9]:=

Out[9]=

For a list of two, nothing happens:

In[10]:=

Out[10]=

Figure out after how many out shuffles a list of size L returns to its original order:

In[11]:=

For lists of even length, the number of shuffles to return to the original order is known analytically:

In[12]:=

Out[12]=

In[13]:=

Out[13]=

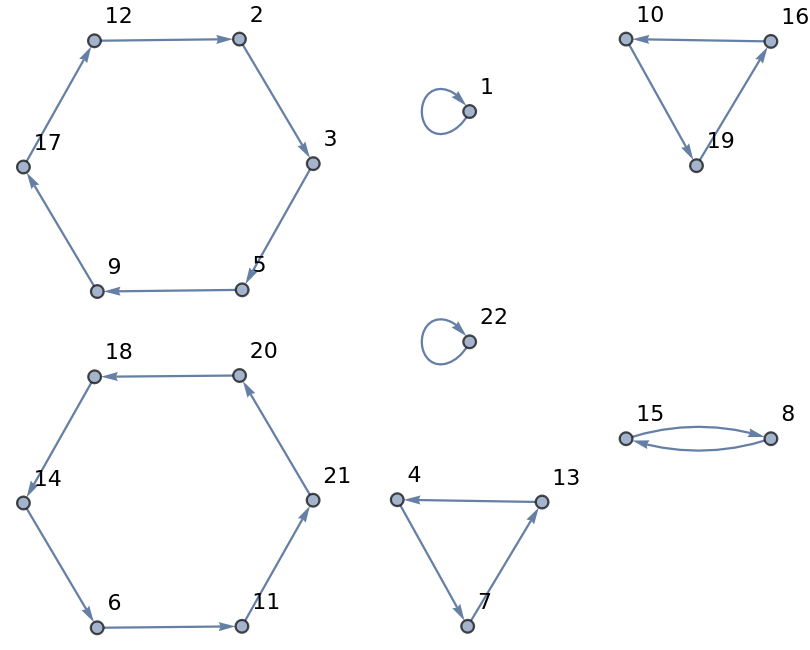
Visualize how the positions of items are changed for a list of length 22 in the form of a Graph:

In[14]:=

t = Range[22];
edges = Thread[t -> Ordering[ResourceFunction["OutShuffle"][t]]];
Graph[edges, VertexLabels -> "Name"]

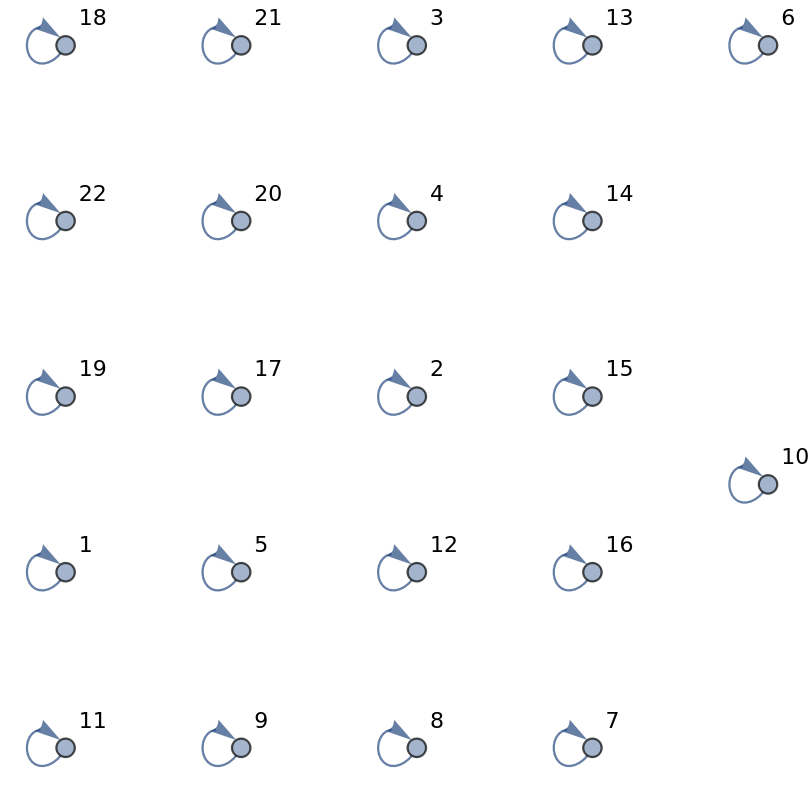
Confirm that six nested out shuffles return the list of 22 items to the original order:

In[15]:=

t = Range[22];
edges = Thread[t -> Ordering[ResourceFunction["OutShuffle"][t, 6]]];
Graph[edges, VertexLabels -> "Name"]

Possible Issues (1)

Zero iterations returns the original list:

In[16]:=

Out[16]=

Neat Examples (1)

Plot how many out shuffles are needed to return to the original order for a list of length L:

In[17]:=

$howManyIterations[n_] := Length[NestWhileList[ResourceFunction["OutShuffle"], ResourceFunction["OutShuffle"]@Range[n], # =!= Range[n] &]] data = Table[{i, howManyIterations[i]}, {i, 300}]; ListPlot[data, Frame -> True, FrameLabel -> {"L", "Number of shuffles needed"}, PlotRange -> All]$

Out[19]=

Publisher

SHuisman

Requirements

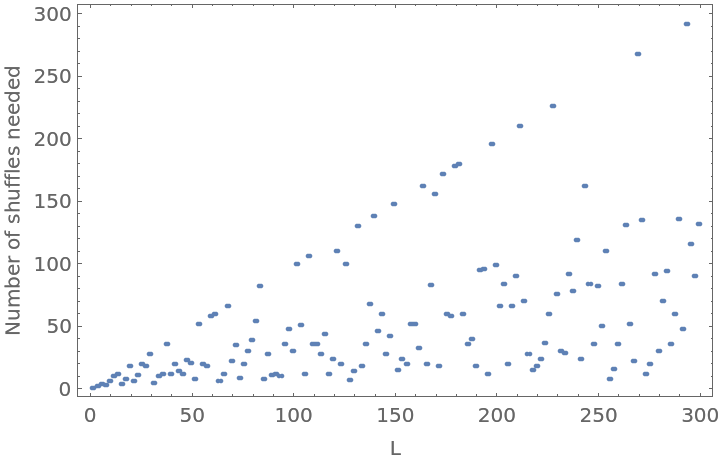Wolfram Language 11.3 (March 2018) or above

Version History

1.0.0 – 10 May 2019

Source Metadata

Citation:
- Conway, J. H. and Guy, R. K. "Fractions Cycle into Decimals." In The Book of Numbers. New York: Springer-Verlag, pp. 163-165, 1996.
  Diaconis, P.; R.L. Graham; W.M. Kantor (1983). "The mathematics of perfect shuffles" (PDF). Advances in Applied Mathematics. 4 (2): 175–196. doi:10.1016/0196-8858(83)90009-X.

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

OutShuffle

Details and Options