Function Repository Resource:

SubscriptToSymbol

Source Notebook

Convert subscripted symbols into indexed symbols

Contributed by: E. Chan-López & Iván Bustamante Romero

ResourceFunction["SubscriptToSymbol"][expr]

converts subscripted symbols within expr to non-subscripted forms.

Details

The non-subscripted form of Subscript[x,y] is the symbol xy. If a value exists for xy, it will be inherited.

ResourceFunction["SubscriptToSymbol"] does not act on standard symbols or numbers; it merely returns them.

ResourceFunction["SubscriptToSymbol"] does not act on protected heads of functions.

ResourceFunction["SubscriptToSymbol"] can be used on matrices and arrays.

Examples

Basic Examples (2)

Use SubscriptToSymbol with a subscripted symbol:

In[1]:=

Out[1]=

Use SubscriptToSymbol with a list of unprotected indexed symbols:

In[2]:=

Out[2]=

In[3]:=

Out[3]=

In[4]:=

$ResourceFunction[ "SubscriptToSymbol"][{Subscript[x, \[Alpha]][t], Subscript[x, \[Beta]][t]}]$

Out[4]=

Scope (6)

Use SubscriptToSymbol with a list of expressions:

In[5]:=

$ResourceFunction[ "SubscriptToSymbol"][{Sin[t], Cos[x], Tan[s], Cot[Subscript[x, 1]], BesselJ[0, Subscript[x, 1][t] + Subscript[x, 2][t]], Csch[(x^(m - 2) - Subscript[x, 3]) (x^(n + 1) + Subscript[x, 2])]}]$

Out[5]=

Use SubscriptToSymbol with indexed capital C related with the default form for the i^th constant C[i]:

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Use SubscriptToSymbol with symbolic matrix:

In[8]:=

Out[9]=

Use SubscriptToSymbol with tensor of rank 3:

In[10]:=

$ResourceFunction["SubscriptToSymbol"]@MatrixForm@D[{\!$ \*SubsuperscriptBox[\(x$, $1$, $2$] \*SubscriptBox[$y$, $1$]\) + Subscript[x, 1], -Subscript[y, 1] \!$\*SubsuperscriptBox[\(x$, $1$, $3$]\) - 2 Subscript[x, 1]}, {{Subscript[x, 1], Subscript[y, 1]}, 2}]$

Out[10]=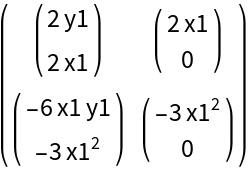

Use SubscriptToSymbol with tensor of rank 4:

In[11]:=

Out[11]=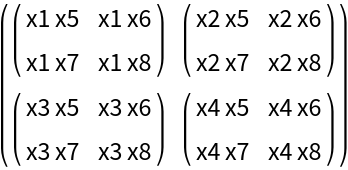

Use SubscriptToSymbol with a nonlinear system of ordinary differential equations:

In[12]:=

$ResourceFunction[ "SubscriptToSymbol"]@{Subscript[x, 1]'[t] == -Subscript[x, 2][t] - Subscript[x, 1][t]^2, Subscript[x, 2]'[t] == 2 Subscript[x, 1][t] - Subscript[x, 2][t]^3}$

Out[12]=

Use SubscriptToSymbol with a system of partial differential equations:

In[13]:=

$ResourceFunction["SubscriptToSymbol"]@{\!$ \*SubscriptBox[\(\[PartialD]$, $t$]$ \(\*SubscriptBox[\(u$, $1$]\)[t, x]\)\) == \!$ \*SubscriptBox[\(\[PartialD]$, $x$]$(\(( \(\*SubscriptBox[\(u$, $2$]\)[t, x] - 1)\)\ \*SubscriptBox[$\[PartialD]$, $x$] $\*SubscriptBox[\(u$, $1$]\)[t, x])\)\) + (16 x t - 2 t - 16 (Subscript[u, 2][t, x] - 1)) (Subscript[u, 1][t, x] - 1) + 10 x E^(-4 x), \!$ \*SubscriptBox[\(\[PartialD]$, $t$]$ \(\*SubscriptBox[\(u$, $2$]\)[t, x]\)\) == \!$ \*SubscriptBox[\(\[PartialD]$, ${x, 2}$]$ \(\*SubscriptBox[\(u$, $2$]\)[t, x]\)\) + \!$ \*SubscriptBox[\(\[PartialD]$, $x$]$ \(\*SubscriptBox[\(u$, $1$]\)[t, x]\)\) + 4 Subscript[u, 1][t, x] - 4 + x^2 - 2 t - 10 t E^(-4 x)}$

Out[13]=

Applications (3)

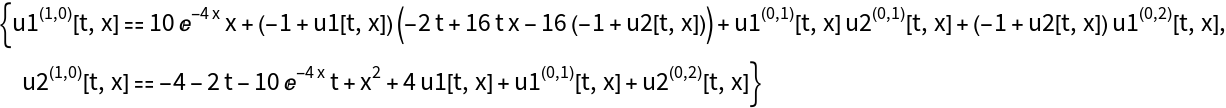Format a symbolic polynomial:

In[14]:=

$polynomial[var_, coeff_Symbol, n_Integer?NonNegative] := Sum[Subscript[coeff, n - k] var^k, {k, 0, n}]$

In[15]:=

Out[15]=

Format a matrix:

In[16]:=

Out[16]=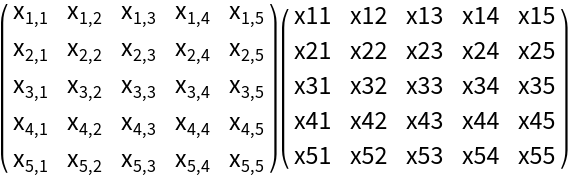

Define a function for making a Vandermonde matrix:

In[17]:=

Format a Vandermonde matrix:

In[18]:=

Out[18]=

Properties and Relations (3)

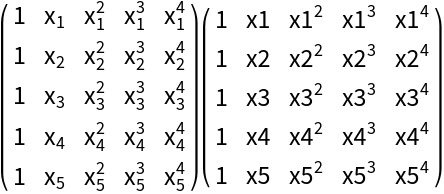Use SubscriptToSymbol with the resource function HurwitzMatrix:

In[19]:=

$ResourceFunction["HurwitzMatrix"][\!$ \*UnderoverscriptBox[\(\[Sum]$, $k = 0$, $7$]$C[k] \*SuperscriptBox[\(x$, $k$]\)\), x]; MatrixForm@%$

Out[20]=

In[21]:=

Out[21]=

Use SubscriptToSymbol with the resource functions SymbolToSubscript and HurwitzMatrix:

In[22]:=

$mat = ResourceFunction["HurwitzMatrix"][\!$ \*UnderoverscriptBox[\(\[Sum]$, $k = 0$, $7$]$ToExpression["\<C\>" <> ToString[k]] \*SuperscriptBox[\(x$, $k$]\)\), x] // MatrixForm$

Out[22]=

In[23]:=

Out[23]=

Convert back to standard symbols:

In[24]:=

Out[24]=

Use SubscriptToSymbol with the resource function SolutionRulesToFunctions:

In[25]:=

$ResourceFunction["SubscriptToSymbol"]@ ResourceFunction["SolutionRulesToFunctions"][\[Theta][t] -> Subscript[\[Theta], 0] + t Subscript[\[Omega], 0] + ( g t^2 Sin[\[Alpha]])/(3 R)]$