Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
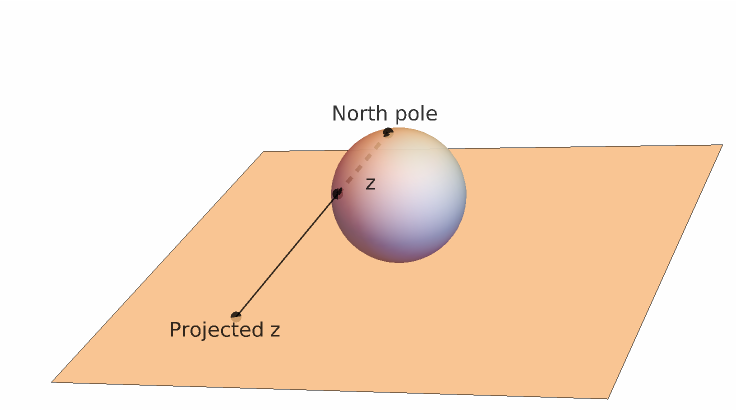
Compute the stereographic projection from the unit sphere to a plane
ResourceFunction["StereographicProjection"][p] computes the stereographic projection of the point p on the unit sphere to the plane. |
An array of points:
| In[1]:= |
|
Stereographic projection:
| In[2]:= |
![Graphics3D[{Blue, Point[Append[ResourceFunction["StereographicProjection"][#], -1] & /@
points], Green, Point[points], Opacity[.5], Red, Sphere[]}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/0df/0dff73c4-1c10-4e2c-8473-c6c4ac92ccf8/10729e71b539a6ad.png)
|
| Out[2]= |
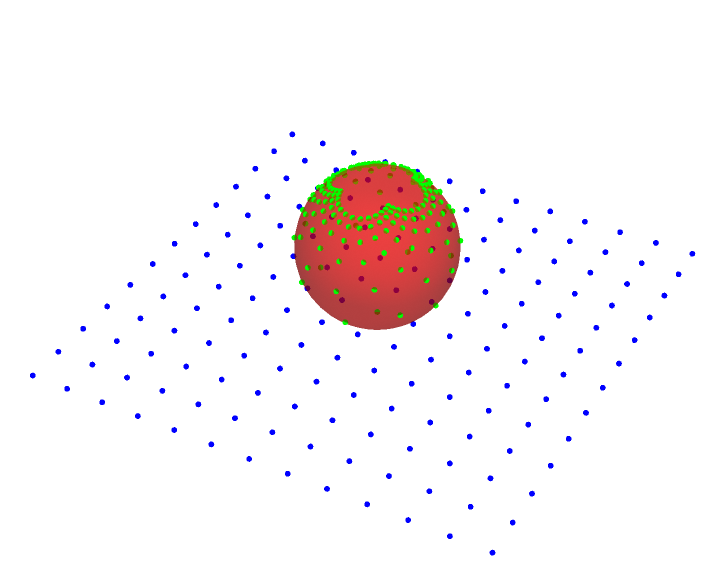
|
The spherical loxodrome becomes the logarithmic spiral:
| In[3]:= |
|
| Out[3]= |
|
Plot of the the logarithmic spiral:
| In[4]:= |
|
| Out[4]= |
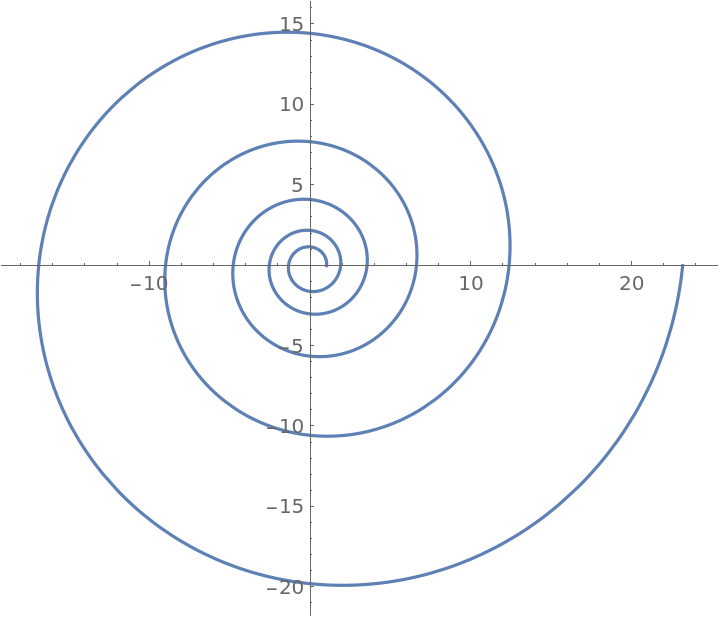
|
Stereographic projection of a rotated loxodrome, used for 3D printing:
| In[5]:= |
![Manipulate[Module[{lox, proj}, lox = ResourceFunction[
ResourceObject[
Association[{
"Name" -> "ApproximatedCurve", "ShortName" -> "ApproximatedCurve", "UUID" -> "6f76840e-ca49-453f-b718-9ebcaeb2881b", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Get an approximation to a parametric curve",
"RepositoryLocation" -> URL[
"https://www.wolframcloud.com/objects/resourcesystem/api/1.\
0"], "SymbolName" -> "FunctionRepository`$\
549444ae0332467fb446b0981ec4a231`ApproximatedCurve", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/1062a39e-e8ea-4b37-bc78-\
8718bdc1c0ed"]}], {ResourceSystemBase -> Automatic}]][
RotationMatrix[\[CurlyPhi], {1, 0, 0}].{Sin[t], -t/4, -Cos[t]}/
Sqrt[1 + (t/4)^2], {t, -100, 100, 2000}, "Coordinates"]; proj = (Append[
ResourceFunction["StereographicProjection"][##1], -1] &) /@ lox; Graphics3D[{Sphere[], InfinitePlane[{{0, 0, -1}, {0, 1, -1}, {1, 0, -1}}], Line[lox], Line[proj]}, PlotRange -> {{-4, 4}, {-4, 4}, {-1, 1}}, Boxed -> False]], {\[CurlyPhi], 0., \[Pi] - \[Pi]/12, \[Pi]/12}]](https://www.wolframcloud.com/obj/resourcesystem/images/0df/0dff73c4-1c10-4e2c-8473-c6c4ac92ccf8/78ff12311116919e.png)
|
| Out[5]= |
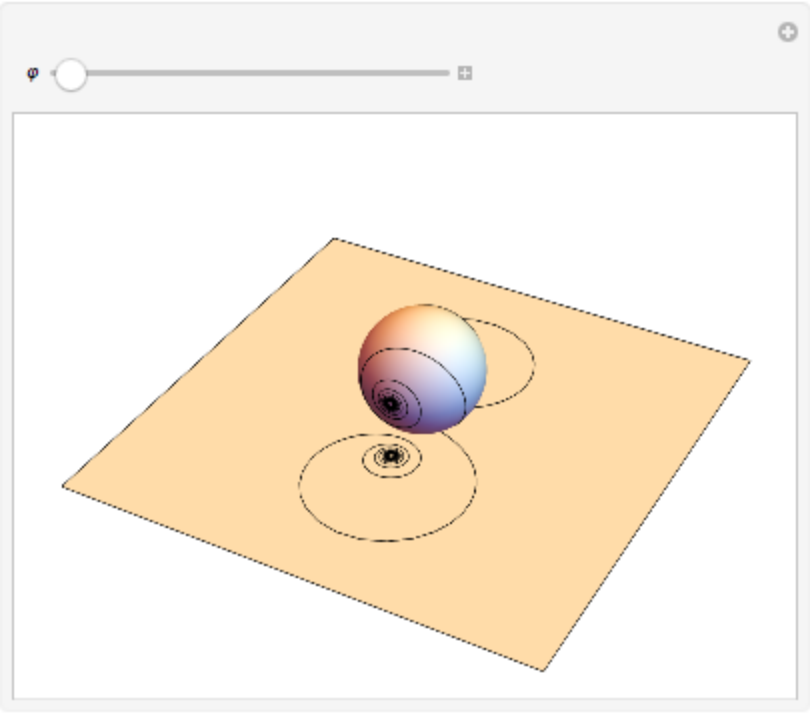
|
The inverse function:
| In[6]:= |
|
| Out[6]= |
|
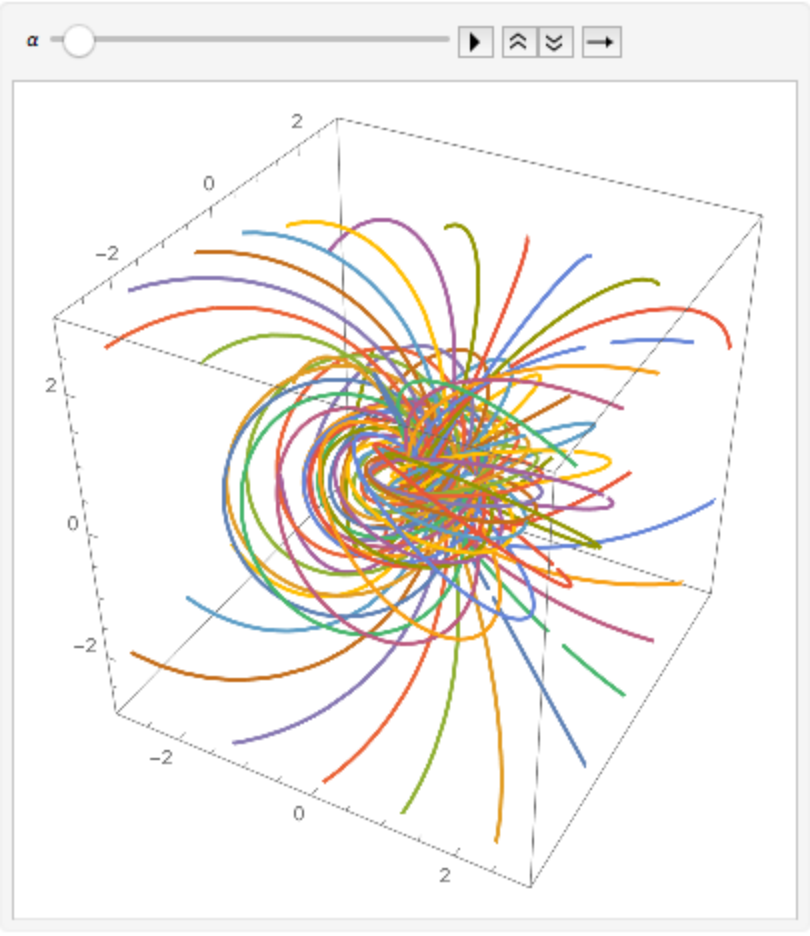
When applying a 4D to 3D stereographic projection to a Hopf fibration, a Clifford torus is generated:
| In[7]:= |
![HopfInverse[\[Theta]_, \[Phi]_, \[Psi]_] := {Cos[\[Phi]/
2] Cos[\[Psi]], Cos[\[Phi]/2] Sin[\[Psi]], Cos[\[Theta] + \[Psi]] Sin[\[Phi]/2], Sin[\[Theta] + \[Psi]] Sin[\[Phi]/2]};
Ryw[\[Theta]_] := RotationMatrix[\[Theta], {{0, 0, 0, 1}, {0, 1, 0, 0}}];
Animate[ParametricPlot3D[
Evaluate[Flatten[
Table[ResourceFunction["StereographicProjection"][
Ryw[\[Alpha]].HopfInverse[\[Theta], \[Phi], \[Psi]]], {\[Phi], Pi/4, 3 Pi/4, Pi/4}, {\[Theta], 0.0, 2 Pi, Pi/9}], 1]], {\[Psi],
Pi/50, 2 Pi}, PlotRange -> 3, PerformanceGoal -> "Speed"], {{\[Alpha], 0}, 0, \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/0df/0dff73c4-1c10-4e2c-8473-c6c4ac92ccf8/05dde2e25a7cf918.png)
|
| Out[7]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License